Robust and Communication-Efficient Federated Learning From Non-i.i.d. Data 论文阅读笔记

1 Introduction

联邦学习的训练过程包括设备下载模型，本地训练模型，将训练得到的模型更新或者模型发送到服务端进行聚合.传输数据的比特数为

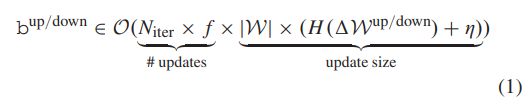
2 Challenge

在介绍压缩传输数据量的方法前,我们首先介绍会在联邦学习压缩传输数据方面的挑战.

• 数据分布之间的不平衡和non-iid
• 数量极大的客户端
• 参数服务器进行聚合
• 部分客户端参与
• 电力和存储受限
  因此,用于联邦学习的通信压缩算法需要满足以下要求:
• R1:同时压缩上传和下载数据量
• R2:可适用于不平衡\non-iid的数据分布
• R3:可适用于大规模客户端和部分客户端参与

3 Contribution

现有的压缩算法基本都不能同时满足上述要求

我们将表明能够压缩上游和下游通信的方法对non-iid数据分布非常敏感，而对此类数据更健壮的方法不会压缩下游数据。然后，我们将着手为联邦学习构建一种新的高效通信协议，该协议可以解决这些问题并满足（R1）–（R3）。我们提供了我们的方法的收敛性分析以及在四种不同的神经网络体系结构和数据集上的广泛经验结果，这些结果表明，稀疏三元压缩（STC）协议优于现有压缩方案，因为它需要较少的梯度数据和通信数据量就能收敛到给定的目标精度,这些结果也扩展到iid分布情况。

4 Limitations of Existing Compression Methods

现有的压缩算法都是假设iid分布的数据,也就是说认为本地梯度是对全局梯度的无偏估计,即

$p_i$为客户端i的数据分布,$R(\mathcal{W})$为全数据的经验风险函数,但这种假设在联邦学习中通常是不成立,一般来说，我们只能希望所有分布的均值是无偏的,即

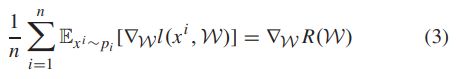
5 Sparse Ternary Compression

我们通过实验发现在现有的压缩算法中,tok-k稀疏化算法对于FL模型的收敛影响最小,因此我们从top-k稀疏算法开始设计我们的算法.为了将top-k算法应用于FL中,我们需要先解决以下三个问题:

• 通过对权重更新的量化和无损编码进一步提高通信效率
• 我们会设计下载的压缩通信
• 我们将实现一个缓存机制,以在客户端部分参与的情况下保持客户端同步.

三元化权重更新

我们将筛选出来的top-k稀疏元素进行量化,具体算法如下所示.

我们使用现有的框架来证明STC算法在标准假设下的收敛性,证明依赖于由压缩因子引起的扰动的限定,我们使用如下的定义来表示该限定


我们假设训练的目标函数$f$是$L-$平滑且$\mu -$强凸的,$\mathbb{E}||\Delta \mathcal{W}|{|}^2\le G^2$且更新规则为:

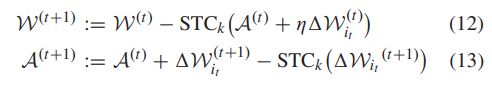
则收敛为

拓展到下载通信

我们使用的聚合算法为

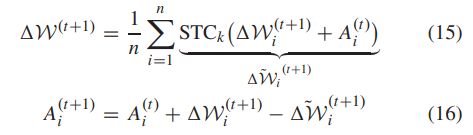
计算得到的更新$\Delta {\mathcal{W}}^{(t+1)}$可能是稠密向量,为了避免这种问题,我们采用如下的压缩

客户端和服务端的累积更新分别为

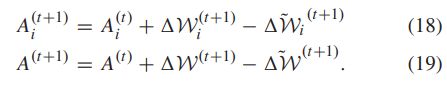
用于部分客户参与的权重更新缓存

由于模型下载的时候只下载模型的更新,而不下载完整的模型,因此只有部分客户端参与训练的时候,客户端之间的模型同步是一个挑战.为了解决这个问题,我们设计了一个在服务端使用的缓存机制.该机制具体流程如下.
我们假设最近的$\tau$次更新为$\{\Delta {\mathcal{W}}^{(t)}|t=T-1,...,T-\tau \}$,服务端会缓存这些更新所有的部分和$\{P^{(s)}={\sum }_{t=1}^s{\Delta \mathcal{W}}^{(T-t)}|s=1,...,\tau \}$,以及一个全局模型${\mathcal{W}}^{(T)}$,每个客户端在参与下轮训练前需要根据其略过的更新次数决定先下载$P^{(s)}$或${\mathcal{W}}^{(T)}$.

无损编码

我们在上传的时候只需要上传非零元素及其符号,并且需要上传该元素的位置,与其传递非零元素的绝对位置,不如传递它们之间的距离.我们假设稀疏化后有$k=p|W|$个元素非零,距离大致呈几何分布,成功概率等于稀疏率p,因此我们使用Golomb编码来进行编码.