Android 启动优化(二) - 拓扑排序的原理以及解题思路,android编程
示例 2
1输入: 4, [[1,0],[2,0],[3,1],[3,2]]
2输出: [0,1,2,3] or [0,2,1,3]
3解释: 总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
4 因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
这道题,很明显,看起来可以有有向无环图的解法来解决
BFS 算法
题目分析
我们首先引入有向图 描述依赖关系
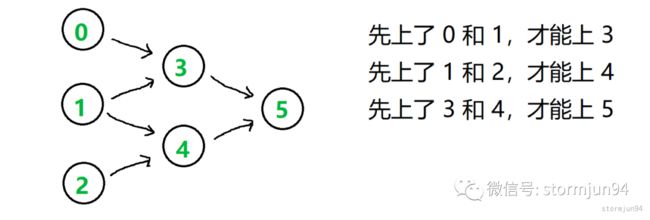
示例:假设 n = 6,先决条件表:[ [3, 0], [3, 1], [4, 1], [4, 2], [5, 3], [5, 4] ]
-
0, 1, 2 没有先修课,可以直接选。其余的,都要先修 2 门课
-
我们用 有向图 描述这种 依赖关系 (做事的先后关系):
在有向图中,我们知道,有入度和出度概念:
如果存在一条有向边 A --> B,则这条边给 A 增加了 1 个出度,给 B 增加了 1 个入度。所以顶点 0、1、2 的 入度为 0。顶点 3、4、5 的 入度为 2
BFS 前准备工作
-
我们关心 课程的入度 —— 该值要被减,要被监控
-
我们关心 课程之间的依赖关系 —— 选这门课会减小哪些课的入度
-
因此我们需要合适的数据结构,去存储这些关系,这个可以通过哈希表
解题思路
-
维护一个 queue,里面都是入度为 0 的课程
-
选择一门课,就让它出列,同时 查看哈希表,看它 对应哪些后续课
-
将这些后续课的 入度 - 1,如果有减至 0 的,就将它推入 queue
-
不再有新的入度 0 的课入列 时,此时 queue 为空,退出循环
1 private class Solution {
2 public int[] findOrder(int num, int[][] prerequisites) {
3
4 // 计算所有节点的入度,这里用数组代表哈希表,key 是 index, value 是 inDegree[index].实际开发当中,用 HashMap 比较灵活
5 int[] inDegree = new int[num];
6 for (int[] array : prerequisites) {
7 inDegree[array[0]]++;
8 }
9
10 // 找出所有入度为 0 的点,加入到队列当中
11 Queue queue = new ArrayDeque<>();
12 for (int i = 0; i < inDegree.length; i++) {
13 if (inDegree[i] == 0) {
14 queue.add(i);
15 }
16 }
17
18 ArrayList result = new ArrayList<>();
19 while (!queue.isEmpty()) {
20 Integer key = queue.poll();
21 result.add(key);
22 // 遍历所有课程
23 for (int[] p : prerequisites) {
24 // 改课程依赖于当前课程 key
25 if (key == p[1]) {
26
《Android学习笔记总结+最新移动架构视频+大厂安卓面试真题+项目实战源码讲义》
【docs.qq.com/doc/DSkNLaERkbnFoS0ZF】 完整内容开源分享
// 入度减一
27 inDegree[p[0]]–;
28 if (inDegree[p[0]] == 0) {
29 queue.offer(p[0]); // 加入到队列当中
30 }
31 }
32 }
33 }
34
35 // 数量不相等,说明存在环
36 if (result.size() != num) {
37 return new int[0];
38 }
39
40 int[] array = new int[num];
41 int index = 0;
42 for (int i : result) {
43 array[index++] = i;
44
45 }
46
47 return array;
48 }
49 }
DFS 解法
算法思想
-
对图执行深度优先搜索。
-
在执行深度优先搜索时,若某个顶点不能继续前进,即顶点的出度为0,则将此顶点入栈。
-
最后得到栈中顺序的逆序即为拓扑排序顺序。
1// 方法 2:邻接矩阵 + DFS 由于用的数组,每次都要遍历,效率比较低
2 public int[] findOrder(int numCourses, int[][] prerequisites) {
3 if (numCourses == 0) return new int[0];
4 // 建立邻接矩阵
5 int[][] graph = new int[numCourses][numCourses];
6 for (int[] p : prerequisites) {
7 graph[p[1]][p[0]] = 1;
8 }
9 // 记录访问状态的数组,访问过了标记 -1,正在访问标记 1,还未访问标记 0
10 int[] status = new int[numCourses];
11 Stack stack = new Stack<>(); // 用栈保存访问序列
12 for (int i = 0; i < numCourses; i++) {
13 if (!dfs(graph, status, i, stack)) return new int[0]; // 只要存在环就返回
14 }
15 int[] res = new int[numCourses];
16 for (int i = 0; i < numCourses; i++) {
17 res[i] = stack.pop();
18 }
19 return res;
20 }
21
22 private boolean dfs(int[][] graph, int[] status, int i, Stack stack) {
23 if (status[i] == 1) return false; // 当前节点在此次 dfs 中正在访问,说明存在环
24 if (status[i] == -1) return true;
25
26 status[i] = 1;
27 for (int j = 0; j < graph.length; j++) {
28 // dfs 访问当前课程的后续课程,看是否存在环
29 if (graph[i][j] == 1 && !dfs(graph, status, j, stack)) return false;
30 }
31 status[i] = -1; // 标记为已访问
32 stack.push(i);