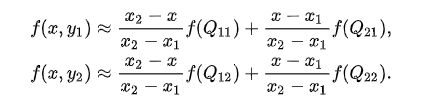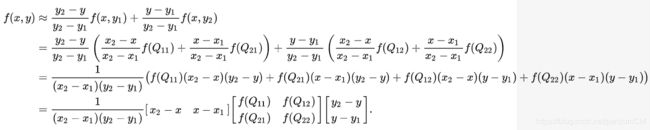CV — 双线性插值算法，python实现，opencv（resize）源码分析

CV — 双线性插值算法

一、概念

• 双线性插值：

  • 双线性插值，又称为双线性内插。在数学上，双线性插值是对线性插值在二维直角网格上的扩展，用于对双变量函数（例如 x 和 y）进行插值。其核心思想是在两个方向分别进行一次线性插值。

  • 示例：

    • 附：维基百科–双线性插值：
      

      我们已知函数 f 在 Q₁₁ = (x1，y1)，Q₁₂ = (x1，y2)，Q₂₁ = (x2，y1)，Q₂₂ = (x2，y2) 四个点的值，我们想得到未知函数 f 在点 P = (x，y) 的值。

      • 步骤如下：
        • 首先在 X 方向进行线性插值，得到：
          
        • 然后在 y 方向进行线性插值，得到：
          以上便是采用双线性插值，得到的 P (x，y) 的值 f（x，y)。

    • 注意此处如果先在 y 方向插值、再在 x 方向插值，其结果与按照上述顺序双线性插值的结果是一样的。

二、双线性插值函数

• 插值法是一种根据原图（source）图片信息构造目标图像（destination）的方法。而其中的双线性插值法是一种目前使用较多的插值方法，他在精度和计算量之间有较好的权衡，所以使用较为广泛。

1.最近邻插值法

给定一个图片像素的矩阵，将1个3∗33∗3尺寸的矩阵使用最近邻插值法到4∗4的矩阵
$$\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]\text{\hspace{1em}(src)}$$
⟹
$$\left[\begin{array}{cccc}？& ？& ？& ？\\ ？& ？& ？& ？\\ ？& ？& ？& ？\\ ？& ？& ？& ？\end{array}\right]\text{\hspace{1em}(dst)}$$

原始图片像素矩阵（src）和缩放后图片像素矩阵（dst）的对应对应关系公式如下：$（博客第三部分会对此公式进行优化）$

src_x = dst_x * (src_width / dst_width)
src_y = dst_y * (src_heght / dst_height)

dst[0][0] 对应的src位置如下：
src_x = 0 * (3 / 4) = 0
src_y = 0 * (3 / 4) = 0
所以dst[0][0] = src[src_x][src_y] = src[0][0] = 1

dst[0][1] 对应的src位置如下：
src_x = 0 * (3 / 4) = 0
src_y = 1 * (3 / 4) = 0.75
所以dst[0][0] = src[src_x][src_y] = src[0][0.75]
由于图片像素最小单位是1，所以四舍五入dst[0][1] = src[0][1] = 2

以此类推，最终结果如下：
$$\left[\begin{array}{cccc}1& 2& 3& 3\\ 4& 5& 6& 6\\ 7& 8& 9& 9\\ 7& 8& 9& 9\end{array}\right]\text{\hspace{1em}(dst)}$$

  这是一种最基本、最简单的图像缩放算法，效果也是最不好的，放大后的图像有很严重的马赛克，缩小后的图像有很严重的失真；
效果不好的根源就是其简单的最近邻插值方法引入了严重的图像失真，比如，当由目标图的坐标反推得到的源图的的坐标是一个$浮点数$的时候，采用了$四舍五入$的方法，直接采用了和这个浮点数最接近的象素的值，这种方法是很不科学的，当推得坐标值为 0.75的时候，不应该就简单的取为1，既然是0.75，比1要小0.25 ，比0要大0.75 ,那么目标象素值其实应该根据这个源图中虚拟的点四周的四个真实的点来按照一定的规律计算出来的，这样才能达到更好的缩放效果。

2. 双线性插值法

  双线型内插值算法就是一种比较好的图像缩放算法，它充分的利用了源图中虚拟点四周的四个真实存在像素点的值（灰度值或者RGB值）来共同决定目标图中的一个像素点的值（灰度值或者RGB值），因此缩放效果比简单的最邻近插值要好很多，缩放后图像质量高，不会出现值（灰度值或者RGB值）不连续的情况。

2.1 双线性内插值算法核心

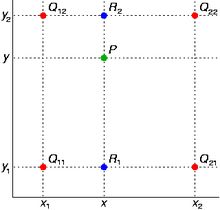
  对于一个目的像素点dst[x][y]，通过反向变换得到的源图像中 浮点坐标为 src[i + u][j + v] (其中i、j均为浮点坐标的整数部分，u、v为浮点坐标的小数部分，是取值[0,1)区间的浮点数)，则这个像素点的值 f(i+u,j+v) 可由原图像中坐标为 (i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)所对应的$最相邻四个像素点的值（灰度值或者RGB值）$决定，即：
f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) + uvf(i+1,j+1)
其中f(i,j)表示源图像(i,j)处的的值（灰度值或者RGB值），以此类推。

2.2 示例

  假如目标图的象素坐标为 （1，1），反推得到的对应于源图的坐标是（0.75 , 0.75）, 这其实只是一个概念上的虚拟象素，实际在源图中并不存在这样一个象素,那么目标图的象素（1，1）的取值不能够由这个虚拟象素来决定，而只能由源图的这四个象素共同决定：（0，0）（0，1）（1，0）（1，1），而由于（0.75,0.75）离（1，1）要更近一些，那么（1,1）所起的决定作用更大一些，这从公式1中的系数uv=0.75×0.75就可以体现出来，而（0.75,0.75）离（0，0）最远，所以（0，0）所起的决定作用就要小一些，公式中系数为(1-u)(1-v)=0.25×0.25也体现出了这一特点。
$即将最近的四个点采用加权平均，离得越近的点的权值越大。$

2.3 算法完整步骤

  假设原始图像大小为size=m×n，其中m与n分别是原始图像的行数与列数。
若图像的缩放因子是t（t>0），则目标图像的大小size=t×m×t×n。对于目标图像的某个像素点P（x，y）通过P*1/t可得到对应的原始图像坐标P’( x1，y1),其中x1=x/t，y1=y/t，由于x1，y1都不是整数所以并不存在这样的点，这样可以找出与它相邻的四个像素点的值（灰度值或者RGB值）、f2、f3、f4，使用双线性插值算法就可以得到这个像素点P’(x1，y1)的值（灰度值或者RGB值），也就是像素点P（x，y）的值（灰度值或者RGB值）。

一个完整的双线性插值算法可描述如下：

1. 通过原始图像和比例因子得到新图像的大小，并用零矩阵初始化新图像。
2. 由新图像的某个像素点（x，y）映射到原始图像(x’，y’)处。
3. 对x’,y’取整得到（xx，yy）并得到(xx，yy)、(xx+1，yy)、（xx，yy+1）和（xx+1，yy+1）的值。
4. 利用双线性插值得到像素点(x，y)的值并写回新图像。

重复步骤2，3 直到新图像的所有像素点写完。

三、opencv（resize）源码分析

  如果采用以上的公式进行编程实现，会发现计算出来的结果会和使用openCV对应的resize（）函数得到的结果完全不一样，而且从直观上观察，图片缩放越小，差异越明显，上面的算法会使缩放之后的图片失真。

3.1 那么opencv到底是做了哪些优化呢？

主要原因： openCV 的 resize 函数对与这个公式进行了改进

src_x = dst_x * (src_width / dst_width)
src_y = dst_y * (src_heght / dst_height)

改为如下：

src_x = (j + 0.5) * float(org_w / dst_w) - 0.5
src_y = (i + 0.5) * float(org_h / dst_h) - 0.5

  通过在公式中进行 $+/-0.5$ 的处理，从来将放缩前后两个图像的几何中心重合，避免图像边缘上部分像素实际上并没有参与计算的问题。
为什么通过 +/-0.5 可以实现将前后两个图像的集合中心重合，本人暂时还没有想明白
本人也是通过手撕opencv的resize.cpp的源码得出这样的结论。

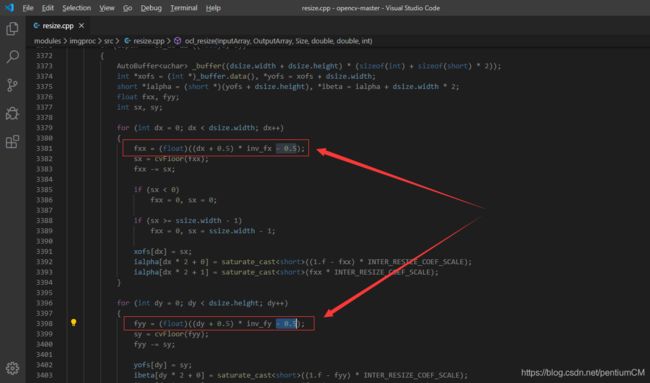
有兴趣的朋友可以一起来研究一下opencv的源码，还是比较有意义的。
github：https://github.com/opencv/opencv

3.2 参考资料

• 维基百科：https://zh.wikipedia.org/zh-cn/%E5%8F%8C%E7%BA%BF%E6%80%A7%E6%8F%92%E5%80%BC
• 博客：
  • 双线性插值算法：
    https://blog.csdn.net/xiaqunfeng123/article/details/17362881
  • opencv处理放缩前后图片中心重合问题：
    https://www.cnblogs.com/funny-world/p/3162003.html

四、python代码实现

#!/usr/bin/env python
# encoding: utf-8
'''
@Author  : pentiumCM
@Email   : [email protected]
@Software: PyCharm
@File    : bilinear_interpolation.py
@Time    : 2020/3/7 11:01
@desc	 : 双线性插值,来调整图像的尺寸
'''

import numpy as np
import cv2

import math


def bilinear(src_img, dst_shape):
    """
    双线性插值法,来调整图片尺寸

    :param org_img: 原始图片
    :param dst_shape: 调整后的目标图片的尺寸
    :return:    返回调整尺寸后的图片矩阵信息
    """
    dst_img = np.zeros((dst_shape[0], dst_shape[1], 3), np.uint8)
    dst_h, dst_w = dst_shape
    src_h = src_img.shape[0]
    src_w = src_img.shape[1]
    # i：纵坐标y，j：横坐标x
    # 缩放因子，dw,dh
    scale_w = src_w / dst_w
    scale_h = src_h / dst_h

    for i in range(dst_h):
        for j in range(dst_w):
            src_x = float((j + 0.5) * scale_w - 0.5)
            src_y = float((i + 0.5) * scale_h - 0.5)
			
			# 向下取整，代表靠近源点的左上角的那一点的行列号	
            src_x_int = math.floor(src_x)
            src_y_int = math.floor(src_y)
            
            # 取出小数部分，用于构造权值
            src_x_float = src_x - src_x_int
            src_y_float = src_y - src_y_int

            if src_x_int + 1 == src_w or src_y_int + 1 == src_h:
                dst_img[i, j, :] = src_img[src_y_int, src_x_int, :]
                continue
            dst_img[i, j, :] = (1. - src_y_float) * (1. - src_x_float) * src_img[src_y_int, src_x_int, :] + \
                               (1. - src_y_float) * src_x_float * src_img[src_y_int, src_x_int + 1, :] + \
                               src_y_float * (1. - src_x_float) * src_img[src_y_int + 1, src_x_int, :] + \
                               src_y_float * src_x_float * src_img[src_y_int + 1, src_x_int + 1, :]
    return dst_img


if __name__ == '__main__':
    img_path = 'F:/experiment/image_identification/License_plate_recognition/Img/1.jpg'

    src = cv2.imread(img_path, cv2.IMREAD_COLOR)
    # 高337 - 宽500
    src_shape = (src.shape[0], src.shape[1])
    # 定义图片缩放后的尺寸
    dst_shape = (100, 400)

    # 图像放缩均采用双线性插值法
    # opencv的放缩图像函数
    resize_image = cv2.resize(src, (400, 100), interpolation=cv2.INTER_LINEAR)

    # 自定义的图像放缩函数
    dst_img = bilinear(src, dst_shape)

    cv2.imwrite('F:/experiment/image_identification/License_plate_recognition/Img/1_new_resize.jpg', resize_image)
    cv2.imwrite('F:/experiment/image_identification/License_plate_recognition/Img/1_new.jpg', dst_img)

直观效果图

如下图所示：

我们要对这一张图片进行缩放：

1. 这是使用双线性插值原始的公式生成的效果图：
   

2. 这是 修改过公式之后 使用0.5坐标平移使缩放前后中心重合的效果图：
   

3. 这是使用 opencv 的 resize 函数进行缩放的效果图：
   

可以看到第一种情况中：图片上的车牌已经出现失真的问题，而优化之后的第二种情况同opencv的resize方式，没有出现失真情况。

精度遗憾

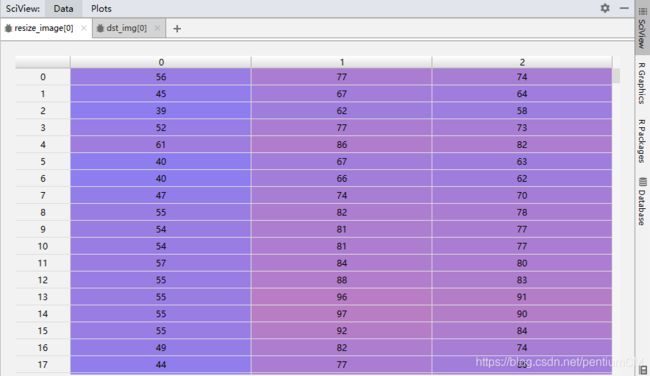
  本人比对了opencv中resize方式的图片矩阵，和自定义算法处理缩放得到的图片矩阵，还是存在矩阵中极少部分中的数据有细微精度偏差。比如这个实验中，图片的RGB值会误差1，这应该是opencv源码中C++部分对于数据进行的精度优化，如果有了解这一误差缘由的大佬，希望得到您的指点。
截选了部分数据供与参考

1. opencv（resize）的图片矩阵数据：
   

2. 自定义的双线性插值算法：