时频分析-傅里叶级数及傅里叶变换、STFT 、小波变换、Wigner-Ville 分布
傅里叶级数
傅里叶生于1768年,死于1830年。傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用.傅里叶级数的公式:
1、把一个周期函数表示成三角级数:
首先,周期函数是客观世界中周期运动的数学表述,如物体挂在弹簧上作简谐振动、单摆振动、无线电电子振荡器的电子振荡等,大多可以表述为:
f(x)=A sin(ωt+ψ)
这里t表示时间,A表示振幅,ω为角频率,ψ为初相(与考察时设置原点位置有关)。
由于许多周期信号并非正弦函数那么简单,如方波、三角波等。傅叶里用一系列的三角函数An sin(nωt+ψ)之和来表示那个较复杂的周期函数f(t),因为正弦函数sin可以说是最简单的周期函数了。
这里,t是变量,其他都是常数。傅里叶把一个周期函数表示成许多正弦函数的线性叠加,这许许多多的正弦函数有着不同的幅度分量(即式中An)、有不同的周期或说是频率(是原周期函数的整数倍,即n)、有不同的初相角(即ψ),当然还有一项常数项(即A0)。要命的是,这个n是从1到无穷大,也就是是一个无穷级数。式子右边一大堆的函数,其实都是最简单的正弦函数,有利于后续的分析和计算。当然,这个式能否成立,关键是级数中的每一项都有一个未知系数,如A0、An等,如果能把这些系数求出来,那么5式就可以成立。当然在5式中,唯一已知的就是原周期函数f(t),那么只需用已知函数f(t)来表达出各项系数。
这样,公式5就可以写成如下公式6的形式:
2、三角函数的正交性:
这是为下一步傅里叶级数展开时所用积分的准备知识。一个三角函数系:1,cosx , sinx , cos2x , sin2x , … , cosnx , sinnx , … 如果这一堆函数(包括常数1)中任何两个不同函数的乘积在区间[-π, π]上的积分等于零,就说三角函数系在区间[-π, π]上正交,即有如下式子:
![]()
以上各式在区间[-π, π]的定积分均为0,第1第2式可视为三角函数cos和sin与1相乘的积分;第3-5式则为sin和cos的不同组合相乘的积分式。除了这5个式子外,不可能再有其他的组合了。注意,第4第5两个式中,k不能等于n,否则就不属于“三角函数系中任意两个不同函数”的定义了,变成同一函数的平方了。但第3式中,k与n可以相等,相等时也是二个不同函数。下面通过计算第4式的定积分来验证其正确性,第4式中二函数相乘可以写成:
![]()
可见在指定[-π, π]的区间里,该式的定积分为0。其他式也可逐一验证。
3、函数展开成傅里叶级数:
先把傅里叶级数表示为下式,即⑥式:
![]()
对⑥式从[-π, π]积分,得:
![]()
这就求得了第一个系数a0的表达式,即最上边傅里叶级数公式里的②式。接下来再求an和bn的表达式。用cos(kωt)乘⑥式的二边得:
![]()
至此,已经求得傅里叶级数中各系数的表达式,只要这些积分都存在,那么⑥式等号右侧所表示的傅里叶级数就能用来表达原函数f(t)。上述过程就是整个傅里叶级数的推导过程。事实上,如果能够写出⑥式,不难求出各个系数的表达式,关键是人们不会想到一个周期函数竟然可以用一些简单的正弦或余弦函数来表达,且这个表达式是一个无穷级数。这当然就是数学家傅里叶的天才之作了,我等只有拼命理解的份了。
综上,傅里叶级数的产生过程可以分为以下三步:
1、设想可以把一个周期函数f(t)通过最简单的一系列正弦函数来表示,即5式;
2、通过变形后用三角级数(含sin和cos)来表示;
3、通过积分,把各未知系数用f(t)的积分式来表达;
4、最后得到的4个表达式就是傅里叶级数公式。
在电子学中,傅里叶级数是一种频域分析工具,可以理解成一种复杂的周期波分解成直流项、基波(角频率为ω)和各次谐波(角频率为nω)的和,也就是级数中的各项。一般,随着n的增大,各次谐波的能量逐渐衰减,所以一般从级数中取前n项之和就可以很好接近原周期波形。这是傅里叶级数在电子学分析中的重要应用。
https://blog.csdn.net/sagittarius_warrior/article/details/78143106
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-3 * np.pi, 3 * np.pi, 1024)
y0 = 0.5 * np.ones(x.size)
y1 = 0.673 * np.cos(x);
y2 = -0.212 * np.cos(3 * x)
y3 = 0.127 * np.cos(5 * x)
y = y0 + y1 + y2 + y3
plt.plot(x, y0, 'g:')
plt.plot(x, y1, 'y:')
plt.plot(x, y2, 'm:')
plt.plot(x, y3, 'c:')
plt.plot(x, y, 'r')
plt.show() 傅里叶变换FFT
FFT (Fast Fourier Transform, 快速傅里叶变换) 是离散傅里叶变换的快速算法,也是数字信号处理技术中经常会提到的一个概念。用快速傅里叶变换能将时域的数字信号转换为频域信号,转换为频域信号后我们可以很方便地分析出信号的频率成分。
傅立叶分析基本上是一种将函数表示为周期性分量之和以及从这些分量中恢复函数的方法。当函数及其傅里叶变换都被离散化的对应物替换时,它被称为离散傅里叶变换(DFT)。DFT已经成为数值计算的支柱,部分原因在于它的计算速度非常快,称为快速傅里叶变换(FFT),高斯(1805)已知并且由Cooley以其当前形式揭示。 Tukey [CT309]。按等人。[NR309]提供了傅里叶分析及其应用的可访问介绍。
由于离散傅里叶变换将其输入分离为在离散频率下贡献的分量,因此它在数字信号处理中具有大量应用,例如用于滤波,并且在这种情况下,变换的离散化输入通常被称为信号。 ,存在于时域中。输出称为频谱或变换,存在于频域中。
import numpy as np#导入一个数据处理模块
import pylab as pl#导入一个绘图模块,matplotlib下的模块
sampling_rate = 50#采样频率为8000Hz
fft_size = 50 #FFT处理的取样长度
# t = np.arange(0, 1.0, 1.0/sampling_rate)#np.arange(起点,终点,间隔)产生1s长的取样时间
# x = np.sin(2*np.pi*156.25*t) + 2*np.sin(2*np.pi*234.375*t) #两个正弦波叠加,156.25HZ和234.375HZ
x = data_singnal_quality_plot(data, 20,40)[0:1400]
x = np.array(x)
# N点FFT进行精确频谱分析的要求是N个取样点包含整数个取样对象的波形。因此N点FFT能够完美计算频谱对取样对象的要求是n*Fs/N(n*采样频率/FFT长度),
# 因此对8KHZ和512点而言,完美采样对象的周期最小要求是8000/512=15.625HZ,所以156.25的n为10,234.375的n为15。
xs = x[:fft_size]# 从波形数据中取样fft_size个点进行运算
xf = np.fft.rfft(xs)/fft_size# 利用np.fft.rfft()进行FFT计算,rfft()是为了更方便对实数信号进行变换,由公式可知/fft_size为了正确显示波形能量
# rfft函数的返回值是N/2+1个复数,分别表示从0(Hz)到sampling_rate/2(Hz)的分。
#于是可以通过下面的np.linspace计算出返回值中每个下标对应的真正的频率:
freqs = np.linspace(0, sampling_rate/2, fft_size/2+1)
# np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)
#在指定的间隔内返回均匀间隔的数字
xfp = 20*np.log10(np.clip(np.abs(xf), 1e-20, 1e100))
#最后我们计算每个频率分量的幅值,并通过 20*np.log10()将其转换为以db单位的值。为了防止0幅值的成分造成log10无法计算,我们调用np.clip对xf的幅值进行上下限处理
#绘图显示结果
pl.figure(figsize=(8,4))
pl.subplot(211)
pl.plot(t[:fft_size], xs)
pl.xlabel(u"Time(S)")
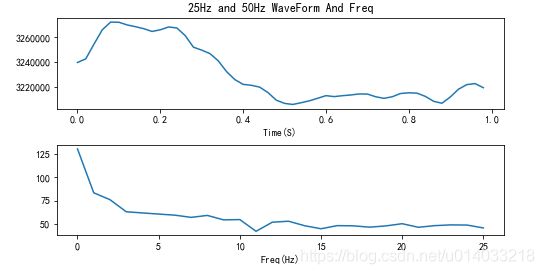
pl.title(u"25Hz and 50Hz WaveForm And Freq")
pl.subplot(212)
pl.plot(freqs, xfp)
pl.xlabel(u"Freq(Hz)")
pl.subplots_adjust(hspace=0.4)
pl.show()信号采样频率和信号频率的关系
对于一个256hz采样频率的信号,每个4个取一个点;消去的频率是64hz;;原理是,:采样频率是256,对应信号的最大频率是128hz,在原信号中每隔4个点取一个,在128hz中对应的就是每隔两个点去一个,去掉的是64hz的信号。
STFT
短时傅里叶变换(Short Time Fourier Transform, STFT) 是一个用于语音信号处理的通用工具.它定义了一个非常有用的时间和频率分布类, 其指定了任意信号随时间和频率变化的复数幅度. 实际上,计算短时傅里叶变换的过程是把一个较长的时间信号分成相同长度的更短的段, 在每个更短的段上计算傅里叶变换, 即傅里叶频谱.
短时傅里叶变换通常的数学定义如下:
其中,
DTFT (Decrete Time Fourier Transform) 为离散时间傅里叶变换. 其数学公式, 如下所示:
其中, x(n) 为在采样数 n 处的信号幅度. ω~ 的定义如下:
实现时, 短时傅里叶变换被计算为一系列加窗数据帧的快速傅里叶变换 (Fast Fourier Transform, FFT),其中窗口随时间 “滑动” (slide) 或“跳跃” (hop) 。
Python 实现
在程序中, frame_size 为将信号分为较短的帧的大小, 在语音处理中, 通常帧大小在 20ms 到 40ms 之间. 这里设置为 25ms, 即 frame_size = 0.025;
frame_stride 为相邻帧的滑动尺寸或跳跃尺寸, 通常帧的滑动尺寸在 10ms 到 20ms 之间, 这里设置为 10ms, 即 frame_stride = 0.01. 此时, 相邻帧的交叠大小为 15ms;
窗函数采用汉明窗函数 (Hamming Function) ;
在每一帧, 进行 512 点快速傅里叶变换, 即 NFFT = 512. 具体程序如下:
import scipy, pylab
def stft(x, fs, framesz, hop):
framesamp = int(framesz*fs)
hopsamp = int(hop*fs)
w = scipy.hanning(framesamp)
X = scipy.array([scipy.fft(w*x[i:i+framesamp])
for i in range(0, len(x)-framesamp, hopsamp)])
return X
def istft(X, fs, T, hop):
x = scipy.zeros(T*fs)
framesamp = X.shape[1]
hopsamp = int(hop*fs)
for n,i in enumerate(range(0, len(x)-framesamp, hopsamp)):
x[i:i+framesamp] += scipy.real(scipy.ifft(X[n]))
return x
if __name__ == '__main__':
f0 = 8 # Compute the STFT of a 440 Hz sinusoid
fs = 50 # sampled at 8 kHz
T = 1 # lasting 5 seconds
framesz = 0.050 # with a frame size of 50 milliseconds
hop = 0.025 # and hop size of 25 milliseconds.
# Create test signal and STFT.
sample_rate, x = 50,data_singnal_quality_plot(data, 0,20)[0:1400]
# t = scipy.linspace(0, T, T*fs, endpoint=False)
# x = scipy.sin(2*scipy.pi*f0*t)
X = stft(x, fs, framesz, hop)
# Plot the magnitude spectrogram.
pylab.figure()
pylab.imshow(scipy.absolute(X.T), origin='lower', aspect='auto',
interpolation='nearest')
pylab.xlabel('Time')
pylab.ylabel('Frequency')
pylab.show()
# Compute the ISTFT.
xhat = istft(X, fs, T, hop)
# Plot the input and output signals over 0.1 seconds.
T1 = int(0.1*fs)
pylab.figure()
pylab.plot(t[:T1], x[:T1], t[:T1], xhat[:T1])
pylab.xlabel('Time (seconds)')
pylab.figure()
pylab.plot(t[-T1:], x[-T1:], t[-T1:], xhat[-T1:])
pylab.xlabel('Time (seconds)')
小波变换walvets
小波变换(WT)分析是近几年比较流行的信号分析方法,它继承并发展了短时傅里叶变换(STFT)局部化的思想,同时又克服了窗口大小不随频率变化等缺点,能够提供一个随频率变化的“时间-频率”窗口,他的主要特点是通过变换能够充分突出问题某些方面的特征,能够对时间(空间)频率的局部化分析,通过伸缩平移运算对信号(函数)进行多尺度细化,最终达到高频处时间细分,低频处频率细分,能够自适应时频信号的要求,从而聚焦到信号的细节。其特点主要包括:正交性、方向选择性、分析数据量小、分辨率可变性等。这种特征使得WT对PPG信号的噪声滤除和波形检测具有良好的特性。
术语(中英对照):
尺度函数 : scaling function (在一些文档中又称为父函数 father wavelet )
小波函数 : wavelet function(在一些文档中又称为母函数 mother wavelet)
连续的小波变换 :CWT
离散的小波变换 :DWT
小波变换的基本知识
不同的小波基函数,是由同一个基本小波函数经缩放和平移生成的。
小波变换是将原始图像与小波基函数以及尺度函数进行内积运算,所以一个尺度函数和一个小波基函数就可以确定一个小波变换
小波变换后低频分量
基本的小波变换函数
以上,就是粗浅意义上傅里叶变换的原理。
如前边所说,小波做的改变就在于,将无限长的三角函数基换成了有限长的会衰减的小波基。
这就是为什么它叫“小波”,因为是很小的一个波嘛~
从公式可以看出,不同于傅里叶变换,变量只有频率ω,小波变换有两个变量:尺度a(scale)和平移量 τ(translation)。尺度a控制小波函数的伸缩,平移量 τ控制小波函数的平移。尺度就对应于频率(反比),平移量 τ就对应于时间。
当伸缩、平移到这么一种重合情况时,也会相乘得到一个大的值。这时候和傅里叶变换不同的是,这不仅可以知道信号有这样频率的成分,而且知道它在时域上存在的具体位置。
而当我们在每个尺度下都平移着和信号乘过一遍后,我们就知道信号在每个位置都包含哪些频率成分。
看到了吗?有了小波,我们从此再也不害怕非稳定信号啦!从此可以做时频分析啦!
做傅里叶变换只能得到一个频谱,做小波变换却可以得到一个时频谱!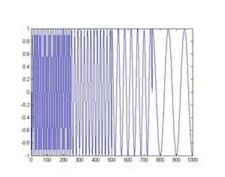
↑:傅里叶变换结果
↑:小波变换结果
小波还有一些好处:
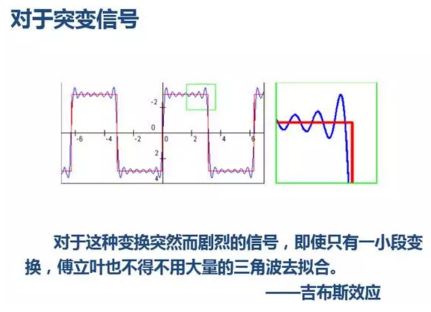
1. 我们知道对于突变信号,傅里叶变换存在吉布斯效应,我们用无限长的三角函数怎么也拟合不好突变信号:
2. 小波可以实现正交化,短时傅里叶变换不能。
以上,就是小波的意义。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
# 画图中文显示
from pylab import mpl
import time
import numpy as np
import matplotlib.pyplot as plt
import pywt
import pywt.data
mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
# Load image
original = pywt.data.camera()
print(original.shape)
print(original)
# Wavelet transform of image, and plot approximation and details
titles = ['Approximation', ' Horizontal detail',
'Vertical detail', 'Diagonal detail']
coeffs2 = pywt.dwt2(original, 'bior1.3')
LL, (LH, HL, HH) = coeffs2
plt.imshow(original)
plt.colorbar(shrink=0.8)
fig = plt.figure(figsize=(12, 3))
for i, a in enumerate([LL, LH, HL, HH]):
ax = fig.add_subplot(1, 4, i + 1)
ax.imshow(a, interpolation="nearest", cmap=plt.cm.gray)
ax.set_title(titles[i], fontsize=10)
ax.set_xticks([])
ax.set_yticks([])
fig.tight_layout()
plt.show()