夜深人静写算法(十九)- 背包总览
文章目录
- 一、前言
- 二、背包问题概览
-
- 1、技能点回顾
- 2、温故而知新
-
- 1)状态转移方程
- 2)时间复杂度
- 3)空间复杂度
- 三、混合背包问题
-
- 1、0/1、完全、多重背包混合
- 2、不同分组背包之间混合
- 四、通用问题概览
-
- 1、容量
-
- 1)如何确定容量
- 2)物品容量为负数时怎么办
- 3)容量为零的分组背包
- 4)多维容量问题
- 2、状态转移
-
- 1)状态转移边界
- 2)状态初始值
- 3、滚动数组
- 4、求解问法
- 5、路径回溯
- 6、 K K K 优解
- 五、背包问题相关题集推荐
-
- 1、入门题
- 2、进阶题
一、前言
本文将对所有背包问题进行一个总结,也是为了致敬 《背包九讲》这部神作。
也有读者和我说自己觉得动态规划实在是太难了,就算能够想到状态表示,也不一定能够推出状态转移方程,就算模糊的有状态转移方程的概念,写的时候一些枚举顺序、初始化什么的也总是会出错,作者也有同感,所以想了一些容易理解的办法,在这篇文章中进行了一个归纳和总结。
总结是一个好习惯,经常做总结的人,运气一定不会太差,每次总结都能够从中学到新的东西,从历史中吸取教训,作为后人的借鉴,于人于己,都是有百利而无一害的!
二、背包问题概览
- 本文主要是对几大类背包问题进行一个总结和回顾,然后对常见问题进行归纳和分析,关于状态转移方程都是一笔带过的,如果想知道详细的推导过程,可以翻看下面链接给出的前置章节。
1、技能点回顾
2、温故而知新
1)状态转移方程
- 每种背包问题的的状态转移方程如下, o p t opt opt 意为 o p t i m a l optimal optimal,即最优的:
【1】0 / 1背包
- 从 “前 i − 1 i-1 i−1 个物品的背包” 中,对第 i i i 个物品进行 “不选” 与 “选” 两种决策: d p [ i ] [ j ] = o p t ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − c i ] + w i ) dp[i][j] = opt(dp[i-1][j], dp[i-1][j-c_i]+w_i) dp[i][j]=opt(dp[i−1][j],dp[i−1][j−ci]+wi)
【2】完全背包
- 从 “前 i i i 种物品的背包” 中,对第 i i i 种物品进行 “不选” 与 “选” 两种决策: d p [ i ] [ j ] = o p t ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − c i ] + w i ) dp[i][j] = opt(dp[i-1][j], dp[i][j-c_i]+w_i) dp[i][j]=opt(dp[i−1][j],dp[i][j−ci]+wi)
【3】多重背包
- 将物品进行二进制拆分后,采用 0/1 背包进行求解: d p [ i ] [ j ] = o p t ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − c i ] + w i ) dp[i][j] = opt(dp[i-1][j], dp[i-1][j-c_i]+w_i) dp[i][j]=opt(dp[i−1][j],dp[i−1][j−ci]+wi)
【4】分组背包 - 每组至多取一个
- 从 “前 k − 1 k-1 k−1 组物品的背包中”,对第 k k k 组的每个物品进行 “不选” 与 “选” 两种决策: d p [ k ] [ j ] = o p t ( d p [ k − 1 ] [ j ] , d p [ k − 1 ] [ j − c i ] + w i ) , k = g i dp[k][j] = opt(dp[k-1][j], dp[k-1][j - c_i] + w_i), k=g_i dp[k][j]=opt(dp[k−1][j],dp[k−1][j−ci]+wi),k=gi
【5】分组背包 - 每组至少取一个
- 拆分成两部分理解:组间至少一个、组内 0/1 背包: d p [ k ] [ j ] = o p t ( d p [ k ] [ j ] , d p [ k − 1 ] [ j − c i ] + w i , d p [ k ] [ j − c i ] + w i ) , k = g i dp[k][j] = opt( dp[k][j], dp[k-1][j-c_i]+w_i, dp[k][j-c_i]+w_i ), k = g_i dp[k][j]=opt(dp[k][j],dp[k−1][j−ci]+wi,dp[k][j−ci]+wi),k=gi
【6】分组背包 - 每组正好取一个
- 从 “前 k − 1 k-1 k−1 组物品的背包中”,对第 k k k 组的每个物品进行 “选” 一个的决策: d p [ k ] [ j ] = o p t ( d p [ k − 1 ] [ j − c i ] + w i ) , k = g i dp[k][j] = opt(dp[k-1][j - c_i] + w_i), k = g_i dp[k][j]=opt(dp[k−1][j−ci]+wi),k=gi
【7】依赖背包 - 主附件依赖
- 先做附件的 0/1 背包(选和不选),再做主件的 0/1 背包(选和不选);
【8】依赖背包 - 树形依赖
- 计算每棵子树的背包,再把子树背包看成物品做分组背包: d p [ u ] [ i ] = o p t v ∈ s o n ( u ) ( d p [ u ] [ i ] , d p [ u ] [ i − j ] + d p [ v ] [ j ] + c o s t u v ) dp[u][i] = opt_{v \in son(u)}(dp[u][i], dp[u][i-j] + dp[v][j] + cost_{uv}) dp[u][i]=optv∈son(u)(dp[u][i],dp[u][i−j]+dp[v][j]+costuv)
- 思考 1:当 j = 0 j=0 j=0 时,这个状态转移方程的正确性如何?(下文会给出答案)
2)时间复杂度
- n n n 代表物品总个数, m m m 代表背包容量;
| 背包类型 | 时间复杂度 |
|---|---|
| 0 / 1 背包 | O ( n m ) O(nm) O(nm); |
| 完全背包 | O ( n m ) O(nm) O(nm); |
| 多重背包 | O ( n m l o g 2 m ) O(nmlog_2m) O(nmlog2m); |
| 分组背包 | O ( n m ) O(nm) O(nm); |
| 主附件依赖背包 | O ( n m ) O(nm) O(nm); |
| 树形依赖背包 | O ( n m 2 ) O(nm^2) O(nm2); |
- 多重背包还有一种用单调队列优化的办法,作者会在介绍单调队列的时候进行讲解;
- 对于分组背包,这里的 n n n 代表的是所有组的物品个数总和;
- 了解时间复杂度的好处是:在问题给出的瞬间,就能大概确定这是个什么类型的问题,比如当 m 为 1 0 9 10^9 109 量级的类似背包的问题就可以确定肯定不是动态规划,需要从搜索或者贪心方向去考虑;而对于树形的结构,并且数据范围都是百量级的,可以往树形依赖背包方向去思考。
3)空间复杂度
- n n n 代表物品总个数, m m m 代表背包容量;
- 注意:这里的空间复杂度代表的是求解过程需要用到的额外空间,不包含给定数据本身的空间;
| 背包类型 | 空间复杂度 |
|---|---|
| 0 / 1 背包 | O ( m ) O(m) O(m); |
| 完全背包 | O ( m ) O(m) O(m); |
| 多重背包 | O ( m ) O(m) O(m); |
| 分组背包 | O ( m ) O(m) O(m); |
| 主附件依赖背包 | O ( m ) O(m) O(m); |
| 树形依赖背包 | O ( n m ) O(nm) O(nm); |
- 0/1 背包 和 完全背包 通过 逆序 和 顺序 求解,将空间降成只和容量有关;
- 多重背包 二进制拆分 后利用 0/1 背包 逆序求解,将空间降成只和容量有关;
- 分组背包中的 至多一个 和 正好一个,都可以类似 0/1 的降维;至少一个的情况可以采用滚动数组降维;
- 主附件依赖 可以通过 滚动数组 进行降维;
- 树形依赖背包 采用的是和分组背包一致的降维方式,因为它本身也是个分组背包,只不过状态转移过程发生在树上;
三、混合背包问题
1、0/1、完全、多重背包混合
2、不同分组背包之间混合
- 即 有些组最多取一个,有些组至少取一个,有些组正好取一个 的情况;
- 观察发现分组背包的状态转移都是发生在两组之间的,所以直接对每一组判断类型,然后按照对应的状态转移方程从上一组的背包进行转移即可;

图三-2-1
四、通用问题概览
1、容量
1)如何确定容量
- 实际问题中,可能会遇到 价格、价值、体积、权值、重量 等名词,到底怎么和背包问题的 “容量” 和 “价值” 进行对应呢?
- 这个问题很好回答, 只要看数据的范围就基本能确定了,“容量” 是一定会映射到数组下标的,所以它的类型一定是整数;而 “价值” 可以是任意类型,而且 “容量” 的范围一般不会超过 1 0 6 10^6 106,再上去的话无论是时间复杂度还是空间复杂度都吃不消,当然不排除有人出一个极限题来恶心人。
【例题1】 n ( n ≤ 100 ) n(n \le 100) n(n≤100) 个物品,第 i i i 个物品的价格为 v i ( 0 ≤ v i ≤ 1 0 8 ) v_i(0 \le v_i \le 10^8) vi(0≤vi≤108),价值为 p i ( p i ≤ 100 ) p_i(p_i \le 100) pi(pi≤100),问想要得到至少为 m ( m ≤ 10000 ) m(m \le 10000) m(m≤10000) 价值的最少价格为多少?
- 这个问题中,“价值” 为背包的容量;
【例题2】 n ( n ≤ 100 ) n(n \le 100) n(n≤100) 个物品,第 i i i 个物品的价格为 v i ( 0 ≤ v i ≤ 100 ) v_i(0 \le v_i \le 100) vi(0≤vi≤100),价值为 p i ( p i ≤ 1 0 8 ) p_i(p_i \le 10^8) pi(pi≤108),问想要用至少 m ( m ≤ 10000 ) m(m \le 10000) m(m≤10000) 的价格,能够买到的最大价值为多少?
2)物品容量为负数时怎么办
- 物品对应的容量为负数时,组合出的背包容量就会为负数;
【例题3】这个国家有 n ( n ≤ 100 ) n(n \le 100) n(n≤100) 种货币。作者的第 i i i 种货币有 c i ( 0 ≤ c i ≤ 100 ) c_i(0 \le c_i \le 100) ci(0≤ci≤100) 个,每个面值是 w i ( 0 ≤ w i ≤ 100 ) w_i(0 \le w_i \le 100) wi(0≤wi≤100)。现在拿着这些货币去商城买东西,商城可以用现有货币进行找回(假设商城足够有钱),问能否买到价值正好为 m m m 的商品。
- 这类问题可以采用一个正数偏移量对状态进行修正,使得映射到数组下标时恒为非负;这个问题是一个物品容量可以为负数的多重背包问题。需要注意的说是,对于容量为负数的物品,如果状态数组采用了降维的情况,那么枚举容量的时候,对 0/1 背包 需要顺序枚举,完全背包 则相反。例如,降维后的 0/1 背包的状态转移方程如下: d p [ j ] = o p t ( d p [ j ] , d p [ j − c i ] + w i ) dp[j] = opt(dp[j], dp[j-c_i]+w_i) dp[j]=opt(dp[j],dp[j−ci]+wi)
- 当 c i < 0 c_i < 0 ci<0 时,状态转移相当于是从 大容量 → \to → 小容量,如果逆序的话,就变成了完全背包,所以需要顺序求解;而完全背包则正好相反。

图四-1-2
3)容量为零的分组背包
【例题4】有 n ( n ≤ 1000 ) n(n \le 1000) n(n≤1000) 个物品和一个容量为 m ( m ≤ 1000 ) m(m \le 1000) m(m≤1000) 的背包。这些物品被分成若干组,第 i i i 个物品属于 g [ i ] g[i] g[i] 组,容量是 c [ i ] ( 0 ≤ c i ≤ 100 ) c[i](0 \le c_i \le 100) c[i](0≤ci≤100),价值是 w i ( 1 ≤ w i ≤ 100 ) w_i(1 \le w_i \le 100) wi(1≤wi≤100),现在需要选择一些物品放入背包,并且每组最多放一个物品,总容量不能超过背包容量,求能够达到的物品的最大总价值。
- 注意,这个问题中,物品容量有可能为 0。
- 对于每组最多取1个的分组背包来说,如果采用了降维,那么就要注意容量为 0 的情况,如下所示的状态转移方程: d p [ j ] = o p t ( d p [ j ] , d p [ j − c i ] + w i ) , k = g i dp[j] = opt(dp[j], dp[j - c_i] + w_i), k=g_i dp[j]=opt(dp[j],dp[j−ci]+wi),k=gi
- 这个状态转移方程表示的是最多取一个的分组背包,并且采用了降维优化,如果 c i = 0 c_i=0 ci=0,就会变成: d p [ j ] = o p t ( d p [ j ] , d p [ j ] + w i ) dp[j] = opt(dp[j], dp[j] + w_i) dp[j]=opt(dp[j],dp[j]+wi)
- 当 o p t = m a x opt=max opt=max,且 w i > 0 w_i > 0 wi>0,若一个组里有 x x x 个 容量为 0 的物品,这 x x x 个物品都会被选进来,和要求相违,所以比较好的做法是采用滚动数组: d p [ c u r ] [ j ] = o p t ( d p [ c u r ] [ j ] , d p [ l a s t ] [ j − c i ] + w i ) , k = g i dp[cur][j] = opt(dp[cur][j], dp[last][j - c_i] + w_i), k=g_i dp[cur][j]=opt(dp[cur][j],dp[last][j−ci]+wi),k=gi
- 这个问题回答了上文的 思考 1。

图四-1-3
4)多维容量问题
- 有些问题中,容量可能是多个维度的,这时候只需要给状态数组加上一维即可。
【例题5】 n ( n ≤ 100 ) n(n \le 100) n(n≤100) 个物品,第 i i i 个物品的重量为 m i m_i mi,体积为 v i v_i vi,权值为 w i w_i wi,现在要取一些物品,使得他们的重量不超过 m m m,体积不超过 v v v,求最大权值。
- 那么定义状态的时候可以定义: d p [ i ] [ j ] [ k ] , i ∈ [ 0 , n ] , j ∈ [ 0 , m ] , k ∈ [ 0 , v ] dp[i][j][k], i \in [0,n], j \in [0,m], k \in [0, v] dp[i][j][k],i∈[0,n],j∈[0,m],k∈[0,v]
- 其中 d p [ i ] [ j ] [ k ] dp[i][j][k] dp[i][j][k] 表示 “前 i i i 个物品中选择一些物品,且重量为 j j j,体积为 k k k 的最大权值”,初始化 d p [ 0 ] [ 0 ] [ 0 ] = 0 dp[0][0][0] = 0 dp[0][0][0]=0,状态转移同样为第 i i i 个物品 “选” 或 “不选”,如下: d p [ i ] [ j ] [ k ] = o p t ( d p [ i − 1 ] [ j ] [ k ] , d p [ i − 1 ] [ j − m i ] [ k − v i ] + w i ) ; dp[i][j][k] = opt(dp[i-1][j][k], dp[i-1][j - m_i][k - v_i] + w_i); dp[i][j][k]=opt(dp[i−1][j][k],dp[i−1][j−mi][k−vi]+wi);
- 另外一种常用的问法是:
【例题6】 n ( n ≤ 100 ) n(n \le 100) n(n≤100) 个物品,第 i i i 个物品的体积为 v i v_i vi,权值为 w i w_i wi,现在要取 k k k 个物品,使得它们的体积不超过 v v v,求最大权值。
- 可以把这里的选择 k k k 个当成是另外一个维度的容量,这个维度下,每个物品的容量为 1,这样就转换成了二维容量问题,一个容量是个数,一个容量是体积,同样可以转换成 d p [ i ] [ j ] [ k ] dp[i][j][k] dp[i][j][k] 状态来求解。状态转移方程为: d p [ i ] [ j ] [ k ] = o p t ( d p [ i − 1 ] [ j ] [ k ] , d p [ i − 1 ] [ j − 1 ] [ k − v i ] + w i ) ; dp[i][j][k] = opt(dp[i-1][j][k], dp[i-1][j - 1][k - v_i] + w_i); dp[i][j][k]=opt(dp[i−1][j][k],dp[i−1][j−1][k−vi]+wi);
- 和上面的状态转移方程的区别是 m i m_i mi 替换成了 1 1 1。

图四-1-4
2、状态转移
1)状态转移边界
- 在进行状态转移方程的推算时,可能会为了状态的边界问题伤透脑筋。
- 这里提供一个方法,进行状态转移的时候先不要去考虑边界问题,直接看这个状态是由哪些状态来的,然后写出来,再去观察状态转移方程,当发现有加减法导致数组下标越界的时候,这时候就把那个作为条件放在枚举的边界中,举个例子: d p [ j ] = o p t ( d p [ j ] , d p [ j − c i ] + w i ) dp[j] = opt(dp[j], dp[j-c_i]+w_i) dp[j]=opt(dp[j],dp[j−ci]+wi)
- 这个是 0 / 1 背包在降维后的状态转移方程, i , j i,j i,j 保证都是大于等于零的,所以唯一会导致下标越界的地方就是: j − c i j-c_i j−ci,所以我们只要保证 j − c i ≥ 0 j-c_i \ge 0 j−ci≥0 恒成立就行。建议结合 物品容量为负数 的情况去思考。

图四-2-1
2)状态初始值
- 状态初始值取决于你如何定义状态,一般有两种定义方法:
- 1)“恰好” 等于给定容量时的最优值;
- 2)小于等于给定容量时的最优值;
- 对于 d p [ i ] [ m ] dp[i][m] dp[i][m] 表示前 i i i 个物品装满容量为 m m m 的背包,我们需要进行初始化的状态为 d p [ 0 ] [ 0... m ] dp[0][0...m] dp[0][0...m];
- 首先,无论是哪种问法, d p [ 0 ] [ 0 ] = 0 dp[0][0] = 0 dp[0][0]=0,因为当一个物品都没有的时候,"恰好"等于 0 和 小于等于 0 的背包价值都是 0;
- 然后,对于 “恰好” 等于 的情况下, d p [ 0 ] [ j ] ( j > 0 ) dp[0][j](j > 0) dp[0][j](j>0) 应该是一个未定义的状态,可以用宏 i n f inf inf 表示;对于 小于等于 的情况, d p [ 0 ] [ j ] = 0 ( j > 0 ) dp[0][j] = 0(j > 0) dp[0][j]=0(j>0),因为一个物品都没有的时候,小于等于容量 j j j 的最优价值就是 0。

图四-2-2
3、滚动数组
- 滚动数组的含义其实是交换,但是叫 交换数组 ,容易引起歧义,而且听起来也很奇怪,感觉是个动词。但是这里的滚动数组其实是个名词,可以滚动的数组,而不是 让数组滚动起来!我去,莫名喜感!
- 滚动数组除了能用在背包问题中,其它动态规划问题也同样适用。
- 令 d p [ c u r ] [ . . . ] dp[cur][...] dp[cur][...] 表示这一行的状态, d p [ l a s t ] [ . . . ] dp[last][...] dp[last][...] 表示上一行的状态, d p [ c u r ] [ . . . ] dp[cur][...] dp[cur][...] 的状态由 d p [ c u r ] [ . . . ] dp[cur][...] dp[cur][...] 或者 d p [ l a s t ] [ . . . ] dp[last][...] dp[last][...] 转移过来,可以写出通用状态转移方程如下: d p [ c u r ] [ . . . ] = o p t ( d p [ c u r ] [ . . . ] , d p [ l a s t ] [ . . . ] ) dp[cur][...] = opt(dp[cur][...], dp[last][...]) dp[cur][...]=opt(dp[cur][...],dp[last][...])
- 并且永远满足 c u r = 1 − l a s t cur = 1 - last cur=1−last,每次求完所有 d p [ c u r ] [ . . . ] dp[cur][...] dp[cur][...] 状态,然后执行
swap(cur,last)进行下标交换就实现了状态的滚动。

图四-3-1
4、求解问法
- 有些问题不是问的最优解,而是问组合出这种问题的方案数。
- 状态转移方程是不变的,比如: d p [ i ] [ j ] = o p t ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − c i ] + w i ) dp[i][j] = opt(dp[i-1][j], dp[i-1][j-c_i]+w_i) dp[i][j]=opt(dp[i−1][j],dp[i−1][j−ci]+wi)
- 如果求最大值,那么: o p t ( x , y ) = m a x ( x , y ) opt(x,y) = max(x, y) opt(x,y)=max(x,y)
- 如果求最小值,那么: o p t ( x , y ) = m i n ( x , y ) opt(x,y) = min(x, y) opt(x,y)=min(x,y)
- 如果求方案数,那么: o p t ( x , y ) = s u m ( x , y ) opt(x,y) = sum(x, y) opt(x,y)=sum(x,y)
5、路径回溯
- 有些问题需要输出问题的一个解,比如 0 / 1 背包问题,我们需要知道是取了哪些物品导致的最大值。
【例题7】 n ( n ≤ 100 ) n(n \le 100) n(n≤100) 个物品,第 i i i 个物品的容量为 c i c_i ci,价值为 w i w_i wi,现在要选一些物品出来,求总容量不超过 m ( m ≤ 10000 ) m(m \le 10000) m(m≤10000) 最大价值和。并且输出取了哪些物品,如果有多种方案,输出任意一种。
- 继续从 0 / 1 背包的状态转移方程出发: d p [ i ] [ j ] = o p t ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − c i ] + w i ) dp[i][j] = opt(dp[i-1][j], dp[i-1][j-c_i]+w_i) dp[i][j]=opt(dp[i−1][j],dp[i−1][j−ci]+wi)
- 我们把 ( i , j ) (i,j) (i,j) 看成是二维空间上的格子, ( i , j ) (i,j) (i,j) 要么从 ( i − 1 , j ) (i-1,j) (i−1,j) 过来,要么从 ( i − 1 , j − c i ) (i-1,j-c_i) (i−1,j−ci) 过来;
- 如图四-5-1所示,竖着的是物品轴,横着的是容量轴,红色方块是我们求得最大价值所在的容量位置,那么必然有一条从 (0,0) 到 红色格子 的唯一路径,而这条唯一路径可以利用状态转移的时候通过记录前驱来获得。
- 然后从红色结点逆序遍历前驱,当前结点和前驱结点容量不等,表明物品被选中了,直到回溯到 ( 0 , 0 ) (0,0) (0,0)。
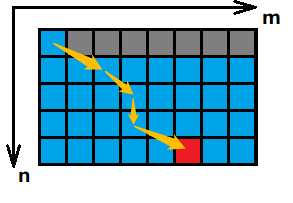
图四-5-1
6、 K K K 优解
【例题8】 n ( n ≤ 100 ) n(n \le 100) n(n≤100) 个物品,第 i i i 个物品的容量为 c i c_i ci,价值为 w i w_i wi,现在要选一些物品出来,求总容量不超过 m ( m ≤ 10000 ) m(m \le 10000) m(m≤10000) 的第 K K K 大价值和 (要求第一大、第二大 … 第 K K K 大的价值和单调递减)。
- 对于 K K K 优解问题,如果对应的最优解问题能够写出状态转移方程,那么 K K K 优解也可以用类似方法来求。
- 对于 0 / 1 背包来说,状态转移方程为: d p [ i ] [ j ] = o p t ( d p [ i − 1 ] [ j ] , d p [ i − 1 ] [ j − c i ] + w i ) dp[i][j] = opt(dp[i-1][j], dp[i-1][j-c_i]+w_i) dp[i][j]=opt(dp[i−1][j],dp[i−1][j−ci]+wi)
- 我们可以把 d p [ i ] [ j ] dp[i][j] dp[i][j] 的定义修改一下,改成 “前 i i i 个物品选择的总容量为 j j j 的 K K K 大权值和”, 那么 d p [ i ] [ j ] dp[i][j] dp[i][j] 可以理解为一个 K K K 维 的向量,而 o p t opt opt 则是对两个 K K K 维向量进行归并排序,并且取前 K K K 大的值。
- 翻译成程序语言就是对状态再扩一维,用 d p [ i ] [ j ] [ k ] dp[i][j][k] dp[i][j][k] 来表示 “前 i i i 个物品选择的总容量为 j j j 的 k k k 大权值和”;
- 则状态转移方程变成: d p [ i ] [ j ] [ . . . ] = o p t ( d p [ i − 1 ] [ j ] [ . . . ] , d p [ i − 1 ] [ j − c i ] [ . . . ] + w i ) dp[i][j][...] = opt(dp[i-1][j][...], dp[i-1][j-c_i][...]+w_i) dp[i][j][...]=opt(dp[i−1][j][...],dp[i−1][j−ci][...]+wi)
- 我们知道,动态规划求最优解的时候,之所以能够求得最优解,是因为它遍历了所有可行方案,从中找到最优解,并且放弃了次优、 K K K 优解,所以我们可以把次优, K K K 优解保留下来,从而通过状态转移求得下一个状态的次优, K K K 优解。
- 举个例子,如图四-6-1,如果想要知道两个数组归并以后的 K K K 大数(这里 K = 3 K = 3 K=3),那么对于任意一个数组,比第 K K K 大的数小的那些数都是无用的,这个可以用贪心简单证明,也就说明了上述动态规划方程的正确性。
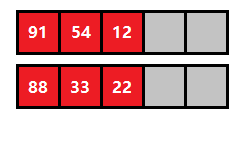
图四-6-1
- 关于 背包问题 的内容到这里就全部结束了。
- 如果还有不懂的问题,可以 想方设法 找到作者的微信进行在线咨询。
五、背包问题相关题集推荐
- 给大家推荐一个比较好的在线评测系统,持续有人在维护,杭州电子科技大学的 OJ:
acm.hdu.edu.cn - 最后,推荐几个在这个 OJ 上比较典型的背包问题。
1、入门题
| 背包类型 | 入门题推荐 |
|---|---|
| 0/1背包 | HDU 2955 Robberies |
| 完全背包 | HDU 1114 Piggy-Bank |
| 多重背包 | HDU 2844 Coins |
| 分组背包 | HDU 1712 ACboy needs your help |
| 混合背包 | HDU 3535 AreYouBusy |
| 二维容量背包 | HDU 2159 FATE |
| 主附件依赖背包 | HDU 3449 Consumer |
| 树形依赖背包 | HDU 4276 The Ghost Blows Light |
| 负容量背包 | HDU 2546 饭卡 |
| 求解方案数 | HDU 2126 Buy the souvenirs |
| K 优解 | HDU 2639 Bone Collector II; |
2、进阶题
| 背包类型 | 进阶题推荐 |
|---|---|
| 0/1背包 | HDU 3466 Proud Merchants |
| 完全背包 | HDU 5534 Partial Tree |
| 多重背包 | HDU 3591 The trouble of Xiaoqian |
| 分组背包 | HDU 3033 I love sneakers! |
| 树形依赖背包 | HDU 4044 GeoDefense |
| 路径回溯 | HDU 3092 Least common multiple |
| K 优解 | HDU 3810 Magina |
| 二维容量分组背包 | HDU 6125 Free from square |
- 背包问题到此就终结了,你学废了吗?
- 本文所有示例代码均可在以下 github 上找到:github.com/WhereIsHeroFrom/Code_Templates
![]()


