《LeetCode零基础指南》(第八讲) 二维数组

零、了解网站

1、输入输出

  对于算法而言，就是给定一些输入，得到一些输出，在一般的在线评测系统中，我们需要自己手写输入输出函数（例如 C语言中的scanf和printf），而在 LeetCode 这个平台，只需要实现它提供的函数即可。函数的传入参数就代表了的算法的输入，而函数的返回值则代表了的算法的输出。

2、刷题步骤

  找到一道题，以 两整数之和 为例，如何把这道题通过呢？如下图所示：

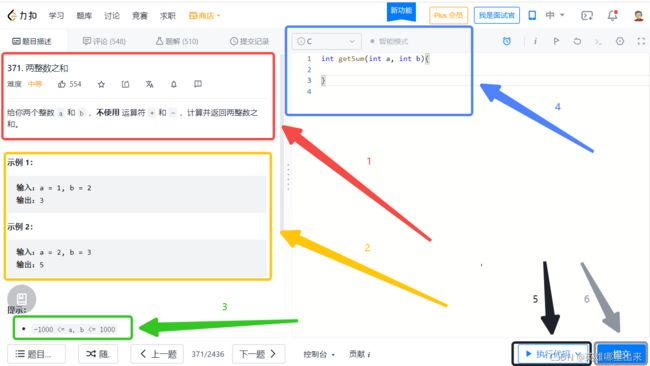
  第 1 步：阅读题目；
  第 2 步：参考示例；
  第 3 步：思考数据范围；
  第 4 步：根据题意，实现函数的功能；
  第 5 步：本地数据测试；
  第 6 步：提交；

---

3、尝试编码

  这个题目比较简单，就是求两个数的和，我们可以在编码区域尝试敲下这么一段代码。

int getSum(int a, int b){
       // (1)
    return a + b;          // (2)
}

• $(1)$ 这里int是C/C++中的一种类型，代表整数，即 Integer，传入参数是两个整数；
• $(2)$ 题目要求返回两个整数的和，我们用加法运算符实现两个整数的加法；

4、调试提交

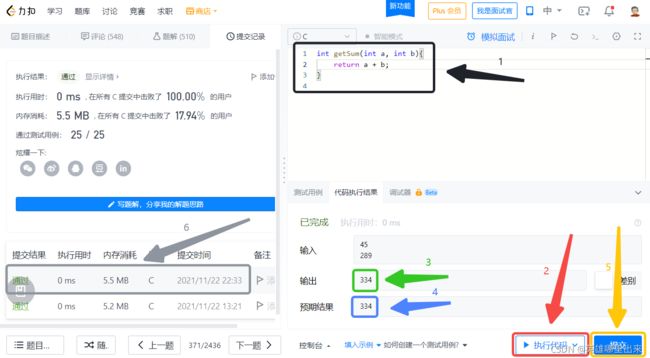
  第 1 步：实现加法，将值返回；
  第 2 步：执行代码，进行测试数据的调试；
  第 3 步：代码的实际输出；
  第 4 步：期望的输出，如果两者符合，则代表这一组数据通过（但是不代表所有数据都能通过哦）；
  第 5 步：尝试提交代码；
  第 6 步：提交通过，撒花 ；

---

  这样，我们就大致知道了一个刷题的步骤了。
  之前我们了解过一维数组，今天我们就来学习一下二维数组，也就是矩阵。

一、概念定义

1、矩阵的定义

  矩阵 $A_{n\times m}$ 的定义是按照长方阵列排列的复数或实数集合，其中 $n$ 代表行数， $m$ 代表列数。如下所示，代表的是一个 $4\times 3$ 的矩阵
$$A_{4\times 3}=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\\ 1& 0& 0\end{array}\right]$$
  在C语言中，我们可以用A[n][m]来代表一个 $n\times m$ 的矩阵，其中A[i][j]代表矩阵第 $i$ 行，第 $j$ 列的值。

2、矩阵的水平翻转

  矩阵的水平翻转，就是将矩阵的每一行的元素进行逆序，矩阵 $A_{4\times 3}$ 水平翻转后的结果如下所示：
$$A_{4\times 3}^{\prime }=\left[\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& 1\\ 0& 0& 1\end{array}\right]$$

3、矩阵的垂直翻转

  矩阵的垂直翻转，就是将矩阵的每一列的元素进行逆序，矩阵 $A_{4\times 3}$ 水垂直翻转后的结果如下所示：
$$A_{4\times 3}^{\prime \prime }=\left[\begin{array}{ccc}1& 0& 0\\ 1& 0& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right]$$

4、矩阵的顺时针旋转

  矩阵的顺时针旋转 90 度，顾名思义，就是绕着垂直屏幕向里的方向，对矩阵进行 90度旋转，这时候行列会交换，所以矩阵 $A_{4\times 3}$ 顺时针90度旋转后的结果如下所示：
$$A_{3\times 4}^{\prime \prime \prime }=\left[\begin{array}{cccc}1& 1& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 1& 0\end{array}\right]$$

5、矩阵的逆时针旋转

  矩阵的逆时针旋转 90 度，我们可以理解成 顺时针旋转 270 度，所以就是做 3 次顺时针旋转 90 度的操作。

6、矩阵的转置

  矩阵的转置，就是对矩阵的主对角线对称的元素进行交换的操作，矩阵 $A_{4\times 3}$ 转置的结果如下：
$$A_{T3\times 4}=\left[\begin{array}{cccc}0& 0& 1& 1\\ 1& 0& 0& 0\\ 0& 1& 0& 0\end{array}\right]$$

7、二维数组

  C语言中，二维数组可以用来描述矩阵，定义如下（3 行 4 列）：

int a[3][4];

  我们也可以将二维数组的元素进行初始化，如下：

int a[3][4] = {
     
	{
     5, 2, 0, 4}
	{
     1, 3, 1, 7}
	{
     4, 0, 0, 9}
};

  由于编译器能够通过后面的初始化列表知道到底有多少个数据元素，所以第一个中括号中的数字可以省略（但是第二个不能省略），如下：

int a[][4] = {
     
	{
     5, 2, 0, 4}
	{
     1, 3, 1, 7}
	{
     4, 0, 0, 9}
};

  当然，我们还可以定义一个大数组，但是只初始化其中几行元素：

int a[100][4] = {
     
	{
     5, 2, 0, 4}
	{
     1, 3, 1, 7}
	{
     4, 0, 0, 9}
};

---

  本质上，你可以把二维数组理解成一个一维数组。只不过一维数组的每一个元素，也是一个一维数组。

8、二维数组的索引

  C语言中数组下标从 0 开始，那么，如果要取得数组a的 $i$ 行 $j$ 列的元素，可以通过a[i][j]进行获取。

9、二维数组的函数传参

  如果你已经了解了一维数组的传参，那么大概应该能猜出二维数组的传参。
  我们来回顾一下一维数组的传参，用的是一个*，如下：

int add(int *nums, int numsSize) {
     
    // ...
}

  那么二维数组的传参，用的就是两个*了，如下：

int diagonalSum(int** mat, int matSize, int* matColSize){
     
}

  其中matSize代表二维数组第一维的大小，也就是可以理解成有多少行；int* matColSize是一个一维数组，代表每一行有多少列，即matColSize[0]代表第 0 行有matColSize[0]列，matColSize[1]代表第 1 行有matColSize[1]列，matColSize[i]代表第 $i$ 行有matColSize[i]列，以此类推。
  由于矩阵的每一列元素都是一样的，所以这类题目中，我们一般可以初始化怎么写：

int diagonalSum(int** mat, int matSize, int* matColSize){
     
    r = matSize;
    c = matColSize[0];
    // TODO
}

  这样写的好处是把变量命名简单化，后续使用的时候不容易出错，让代码更加易读。

二、题目分析

1、统计矩阵中的负数

  给你一个 $m\times n$ 的矩阵 grid，请统计并返回grid中 负数 的数目。

int countNegatives(int** grid, int gridSize, int* gridColSize){
     
    int i, j, ans = 0;              
    int r = gridSize;              // (1)
    int c = gridColSize[0];
    for(i = 0; i < r; ++i) {
     
        for(j = 0; j < c; ++j) {
     
            if(grid[i][j] < 0) {
     
                ++ans;             // (2)
            } 
        }
    }
    return ans;
}

• $(1)$ 初始化矩阵的行列信息；
• $(2)$ 遍历矩阵中的每个元素，对负数进行计数累加；

---

2、矩阵对角线元素的和

  给你一个正方形矩阵mat，请你返回矩阵对角线元素的和。请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。

int diagonalSum(int** mat, int matSize, int* matColSize){
     
    int r = matSize;                 // (1)
    int c = matColSize[0];
    int i;
    int ans = 0;
    for(i = 0; i < r; ++i) {
     
        ans += mat[i][i];            // (2)
    }
    for(i = 0; i < r; ++i) {
     
        if(r-i-1 != i) {
     
            ans += mat[i][r-i-1];    // (3)
        }
    }
    return ans;
}

• $(1)$ 初始化矩阵的行列信息；
• $(2)$ 将主对角线上的和累加；
• $(3)$ 将副对角线上的和累加，注意去掉和主对角线重合的那一个元素；

---

3、最富有客户的资产总量

  给你一个 $mxn$ 的整数网格accounts，其中accounts[i][j]是第 $i$​​​​​​​​​​​​ 位客户在第 $j$ 家银行托管的资产数量。返回最富有客户所拥有的 资产总量 。客户的 资产总量 就是他们在各家银行托管的资产数量之和。最富有客户就是 资产总量 最大的客户。

int maximumWealth(int** accounts, int accountsSize, int* accountsColSize){
     
    int i, j;
    int maxv = -1, maxIdx, sumv;
    for(i = 0; i < accountsSize; ++i) {
     
        sumv = 0;
        for(j = 0; j < *accountsColSize; ++j) {
     
            sumv += accounts[i][j];             // (1)
        }
        if(sumv > maxv) {
     
            maxv = sumv;                        // (2)
            maxIdx = i;
        }
    }
    return maxv;
}

• $(1)$ 累加第 $i$​​​​​​​​​​​​ 位客户的所有资产；
• $(2)$ 选取资产总额最大的客户，更新最大值；

---

4、托普利茨矩阵

  给你一个 $mxn$ 的矩阵 matrix。如果这个矩阵是托普利茨矩阵，返回 true；否则，返回 false。如果矩阵上每一条由左上到右下的对角线上的元素都相同，那么这个矩阵是 托普利茨矩阵。

int checkSame(int** matrix, int sr, int sc, int maxr, int maxc) {
       // (1)
    int step = 0;
    while(1) {
     
        if(sr + step >= maxr) {
     
            break;                                                 // (2)
        }
        if(sc + step >= maxc) {
     
            break;                                                 // (3)
        }
        if(matrix[sr+step][sc+step] != matrix[sr][sc]) {
                // (4)
            return false;
        }
        ++step;                                                    // (5)
    }
    return true;                                                   // (6)
}

bool isToeplitzMatrix(int** matrix, int matrixSize, int* matrixColSize){
     
    int r = matrixSize;
    int c = matrixColSize[0];
    int i;
    for(i = 0; i < c; ++i) {
     
        if( !checkSame(matrix, 0, i, r, c) ) {
                          // (7)
            return false;  
        }        
    }
    for(i = 0; i < r; ++i) {
     
        if( !checkSame(matrix, i, 0, r, c) ) {
                          // (8)
            return false;
        }    
    }
    return true;
}

• $(1)$ checkSame这个函数表示从 $(sr,sc)$ 这个位置往斜下角的元素是否都相等，相等返回true，否则返回false；
• $(2)$ 行越界，直接停下来；
• $(3)$ 列越界，直接停下来；
• $(4)$ 有一个元素和起始元素不相等，则直接返回false；
• $(5)$ 往前走一步；
• $(6)$ break走到的逻辑，则必定是全相等的情况；
• $(7)$ 检查从第一行的每个元素往右下角走的情况；
• $(8)$ 检查从第一列的每个元素往右下角走的情况；

---

三、推荐学习

《算法零基础100讲》
(第3讲) 矩阵

四、课后习题

  从本章开始，九日集训不在淘汰人员，今天的题目不要求全部刷完，可以选择性刷完四题，并且自己有自己的总结，发布完解题报告打卡，即可晋级。
  坚持！加油！你可以的！

序号	题目链接	难度
1	统计有序矩阵中的负数	★☆☆☆☆
2	矩阵对角线元素的和	★☆☆☆☆
3	最富有客户的资产总量	★☆☆☆☆
4	托普利茨矩阵	★☆☆☆☆
5	矩阵中的幸运数	★☆☆☆☆
6	二进制矩阵中的特殊位置	★☆☆☆☆
7	岛屿的周长	★☆☆☆☆
8	翻转矩阵后的得分	★☆☆☆☆

关注公众号 观看 精彩学习视频