【机器学习】机器学习之线性判别分析(LDA)

一、线性判别分析介绍

  线性判别分析(Linear Discriminant Analysis，简称 $LDA$)是一种经典的线性学习方法，亦称"Fisher 判别分析"。

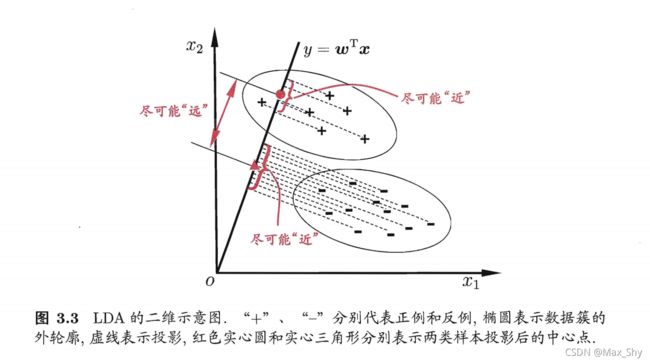
  线性判别分析思想：给定训练样本集，设法将样例投影到一条直线上。使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远；在对新样本进行分类时，将其投影到该直线上，再根据投影点的位置来确定新样本的类别。

二、线性判别分析原理

  给定数据集 $D=\{(x_i\text{xi}{x}_i,y_i){\}}_{i=1}^m,y_i\in \{0,1\}$ ，令$X_i$、${\mu }_i\text{μi}{\mu }_i$、${\sum }_i\text{∑i}{\sum }_i$ 分别表示 $i\in \{0,1\}$ 类示例的集合、均值向量、协方差矩阵。若将数据投影到直线 $\omega \text{ω}\omega$ 上，则两类样本的中心在直线上的投影分别为 ${\omega }^T{\mu }_0\text{ωTμ0}{\omega }^T{\mu }_0$ 和 ${\omega }^T{\mu }_1\text{ωTμ1}{\omega }^T{\mu }_1$ ；若将所有样本点都投影到直线上，则两类样本的协方差分别为 ${\omega }^T{\sum }_0\omega \text{ωT∑0ω}{\omega }^T{\sum }_0\omega$ 和 ${\omega }^T{\sum }_1\omega \text{ωT∑1ω}{\omega }^T{\sum }_1\omega$ 。由于直线处于一维空间，因此 ${\omega }^T{\mu }_0\text{ωTμ0}{\omega }^T{\mu }_0$、${\omega }^T{\mu }_1\text{ωTμ1}{\omega }^T{\mu }_1$ 、${\omega }^T{\sum }_0\omega \text{ωT∑0ω}{\omega }^T{\sum }_0\omega$ 和 ${\omega }^T{\sum }_1\omega \text{ωT∑1ω}{\omega }^T{\sum }_1\omega$ 均为实数。

  要使得同类样例的投影点尽可能接近，所以应让同类样例投影点的协方差尽可能小，即${\omega }^T{\sum }_0\omega +{\omega }^T{\sum }_1\omega \text{ωT∑0ω+ωT∑1ω}{\omega }^T{\sum }_0\omega +{\omega }^T{\sum }_1\omega$ 尽可能小。
  要使得异类样例的投影点尽可能地远，则让类中心之间的距离尽可能大，即 $||{\omega }^T{\mu }_0\text{ωTμ0}{\omega }^T{\mu }_0-{\omega }^T{\mu }_1|{|}_2^2\text{ωTμ1∣∣22}{\omega }^T{\mu }_1|{|}_2^2$ 尽可能大。同时考虑二者，则需要得到的最大化目标为：
$$\begin{array}{rl}J\text{J}J& =\frac{||{\omega }^T{\mu }_0-{\omega }^T{\mu }_1|{|}_2^2}{{\omega }^T{\sum }_0\omega +{\omega }^T{\sum }_1\omega }\\ & =\frac{{\omega }^T({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T\omega }{{\omega }^T({\sum }_0+{\sum }_1)\omega }\end{array}$$

1. 类内散度矩阵（within-class scatter matrix）

  类内散度矩阵用来判断同类样例的投影点之间的距离。
$$\begin{array}{rl}{S}_w& =\sum _0+\sum _1\\ & =\sum _{x\in X_0}(x-{\mu }_0)(x-{\mu }_0{)}^T+\sum _{x\in X_1}(x-{\mu }_1)(x-{\mu }_1{)}^T\end{array}$$

2. 类间散度矩阵（between-class scatter matrix）

  类间散度矩阵用来判断异类样例的投影点之间的距离。
$$S_b=({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T$$

3. 广义瑞利商(generalized Rayleigh quotiet)

  广义瑞利商(generalized Rayleigh quotiet)就是 $LDA$欲最大化的目标。
  使用类内散度矩阵和类间散度矩阵将最大化目标改写为：
$$J\text{J}J=\frac{{\omega }^T{S}_b\omega }{{\omega }^T{S}_w\omega }$$

  $LDA$ 可从贝叶斯决策理论的角度来阐释，并可证明，当两类数据同先验、满足高斯分布且协方差相等时，$LDA$可达到最优分类。

三、sklearn库实现线性判别分析LDA

1. 数据生成

#生成200个三个维度样本
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.datasets import make_classification
x, y = make_classification(n_samples=200, n_features=2, n_redundant=0, n_classes=2, n_informative=2,n_clusters_per_class=2,class_sep =1, random_state =0)
fig = plt.figure()
plt.scatter(x[:, 0], x[:, 1], c=y)

2. 数据处理

#设置分类平滑度
h = .01
#设置X和Y的边界值
x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1
y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1

#使用meshgrid函数返回X和Y两个坐标向量矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max,h), np.arange(y_min, y_max,h))
Z = lda.predict(np.c_[xx.ravel(), yy.ravel()])

3. 数据集划分

from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x, y, random_state=33, test_size=0.25)

4. LDA分类

#使用LDA进行降维
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis 
from sklearn.linear_model import LogisticRegression
lda = LinearDiscriminantAnalysis(n_components=1)

x_train_lda = lda.fit_transform(x_train, y_train)  # LDA是有监督方法，需要用到标签
x_test_lda = lda.fit_transform(x_test, y_test)   # 预测时候特征向量正负问题，乘-1反转镜像

5. 绘制训练集分类图像

#设置colormap颜色
cm_bright = ListedColormap(['#D9E021', '#0D8ECF'])
#绘制数据点
plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train, cmap=cm_bright)
plt.title('Linear Discriminant Analysis Classifiers')
plt.axis('tight')
plt.show()

6. 绘制测试集分类图像

plt.title('Linear Discriminant Analysis Classifiers')
plt.scatter(x_test[:, 0], x_test[:, 1], c=y_test, cmap=cm_bright)
plt.show()

四、总结

  　LDA算法既可以用来降维，也可以用来分类，但是目前来说，主要还是用于降维，和PCA类似，LDA降维基本也不用调参，只需要指定降维到的维数即可。

五、参考

Python机器学习笔记：线性判别分析（LDA）算法