蒟蒻一枚
蒟蒻一枚

CSPJ2021考完了，你，AK了吗？

CSP考完了，祝愿大家都取得理想的成绩~
大家最喜欢的蒟蒻君为大家奉上CSPJ2021题解，大家有哪里不会的可以参考一下 （请AKer们忽略a）
由于时间原因更得确实太晚了请大家原谅
CSPJ2021考完了，你，AK了吗？_第1张图片

❤️rp++

  • T1：分糖果
    • ☀️题目信息
    • ☀️解题思路
      • 题目大意
      • 思路分析：数学方法
    • ☀️代码实现
  • T2：插入排序
    • ☀️题目信息
    • ☀️解题思路
      • 题目大意
      • 36分做法：直接模拟
      • 52分做法：快排优化
      • 76分做法：模拟排序
      • 100分做法1：前后冒泡
      • 100分做法2：线段树维护
    • ☀️代码实现
      • 36分做法：直接模拟
      • 52分做法：快排优化
      • 76分做法：模拟排序
      • 100分做法1：前后冒泡
      • 100分做法2：线段树维护
  • T3： 网络连接
    • ☀️题目信息
    • ☀️解题思路
      • 题目大意
      • 思路分析：大模拟
      • 易错点
        • 易错点1
        • 易错点2
    • ☀️代码实现
  • T4：小熊的果篮
    • ☀️题目信息
    • ☀️解题思路
      • 题目大意
      • 70分做法：模拟
      • 100分做法1：队列维护+模拟
      • 100分做法2：珂朵莉树
    • ☀️代码实现
      • 70分做法：模拟
      • 100分做法：队列维护+模拟
      • 100分做法2：珂朵莉树
  • 附件下载

T1：分糖果

☀️题目信息

题目背景

红太阳幼儿园的小朋友们开始分糖果啦！

题目描述

红太阳幼儿园有 n n n 个小朋友，你是其中之一。保证 n ≥ 2 n \ge 2 n≥2。
有一天你在幼儿园的后花园里发现无穷多颗糖果，你打算拿一些糖果回去分给幼儿园的小朋友们。

由于你只是个平平无奇的幼儿园小朋友，所以你的体力有限，至多只能拿 R R R 块糖回去。

但是拿的太少不够分的，所以你至少要拿 L L L 块糖回去。保证 n ≤ L ≤ R n \le L \le R n≤L≤R。

也就是说，如果你拿了 k k k 块糖，那么你需要保证 L ≤ k ≤ R L \le k \le R L≤k≤R。

如果你拿了 k k k 块糖，你将把这 k k k 块糖放到篮子里，并要求大家按照如下方案分糖果：只要篮子里有不少于 n n n 块糖果，幼儿园的所有 n n n 个小朋友（包括你自己）都从篮子中拿走恰好一块糖，直到篮子里的糖数量少于 n n n 块。此时篮子里剩余的糖果均归你所有——这些糖果是作为你搬糖果的奖励。

作为幼儿园高质量小朋友，你希望让作为你搬糖果的奖励的糖果数量（而不是你最后获得的总糖果数量！）尽可能多；因此你需要写一个程序，依次输入 n , L , R n, L, R n,L,R，并输出出你最多能获得多少作为你搬糖果的奖励的糖果数量。

输入输出格式

输入格式

输入一行，包含三个正整数 n , L , R n, L, R n,L,R，分别表示小朋友的个数、糖果数量的下界和上界。

输出格式

输出一行一个整数，表示你最多能获得的作为你搬糖果的奖励的糖果数量。

输入输出样例

输入样例 #1

7 16 23

输出样例 #1

6

输入样例 #2

10 14 18

输出样例 #2

8

输入样例 #3

见附件中的 candy/candy3.in。

输出样例 #3

见附件中的 candy/candy3.ans。

说明

【样例解释 #1】

拿 $k = 20$ 块糖放入篮子里。

篮子里现在糖果数 20 ≥ n = 7 20 \ge n = 7 20≥n=7，因此所有小朋友获得一块糖；

篮子里现在糖果数变成 13 ≥ n = 7 13 \ge n = 7 13≥n=7，因此所有小朋友获得一块糖；

篮子里现在糖果数变成 KaTeX parse error: Expected 'EOF', got '&' at position 3: 6 &̲lt; n = 7，因此这 6 6 6 块糖是作为你搬糖果的奖励。

容易发现，你获得的作为你搬糖果的奖励的糖果数量不可能超过 6 6 6 块（不然，篮子里的糖果数量最后仍然不少于 n n n，需要继续每个小朋友拿一块），因此答案是 6 6 6。

【样例解释 #2】

容易发现，当你拿的糖数量 k k k 满足 14 = L ≤ k ≤ R = 18 14 = L \le k \le R = 18 14=L≤k≤R=18 时，所有小朋友获得一块糖后，剩下的 k − 10 k - 10 k−10 块糖总是作为你搬糖果的奖励的糖果数量，因此拿 k = 18 k = 18 k=18 块是最优解，答案是 8 8 8。

【数据范围】

测试点 n ≤ n \le n≤ R ≤ R \le R≤ R − L ≤ R - L \le R−L≤
1 1 1 2 2 2 5 5 5 5 5 5
2 2 2 5 5 5 10 10 10 10 10 10
3 3 3 10 3 {10}^3 103 10 3 {10}^3 103 10 3 {10}^3 103
4 4 4 10 5 {10}^5 105 10 5 {10}^5 105 10 5 {10}^5 105
5 5 5 10 3 {10}^3 103 10 9 {10}^9 109 0 0 0
6 6 6 10 3 {10}^3 103 10 9 {10}^9 109 10 3 {10}^3 103
7 7 7 10 5 {10}^5 105 10 9 {10}^9 109 10 5 {10}^5 105
8 8 8 10 9 {10}^9 109 10 9 {10}^9 109 10 9 {10}^9 109
9 9 9 10 9 {10}^9 109 10 9 {10}^9 109 10 9 {10}^9 109
10 10 10 10 9 {10}^9 109 10 9 {10}^9 109 10 9 {10}^9 109

对于所有数据，保证 2 ≤ n ≤ L ≤ R ≤ 10 9 2 \le n \le L \le R \le {10}^9 2≤n≤L≤R≤109。

☀️解题思路

题目大意

这道题作为普及T1还是很凉心滴…
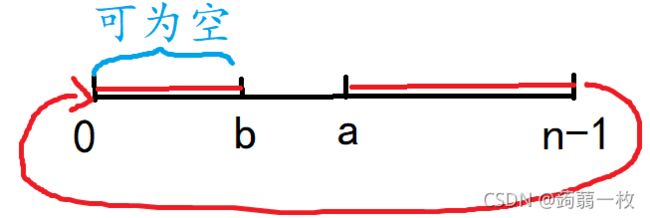
求 max ⁡ l ≤ x ≤ r x ( m o d n ) \displaystyle \max\limits_{l≤x≤r}x\pmod n l≤x≤rmax​x(modn)，或者说是求l≤x≤r时，x%n的最大值。

思路分析：数学方法

首先任意一个数mod n，结果最大也就是n - 1了。
那什么时候答案是n - 1呢？有一下两种情况：

  • [l, r]的长度>=n，即所有符合条件的x mod n可以是[0, n - 1]中的任意数。
  • [l, r]的长度 CSPJ2021考完了，你，AK了吗？_第2张图片

若不符合以上条件，即r - l + 1 < n且l % n <= r % n，答案为r % n。

☀️代码实现

我真是个高质量幼儿园小朋友啊

#include 
using namespace std;
int main() {
     
	int n, l, r;
	cin >> n >> l >> r;
	int a = l % n, b = r % n;
	if (r - l + 1 >= n || b < a) {
     
		cout << n - 1 << '\n';
	} else {
     
		cout << b << '\n';
	}
	return 0;
}

CSPJ2021考完了，你，AK了吗？_第3张图片

T2：插入排序

☀️题目信息

题目描述

插入排序是一种非常常见且简单的排序算法。小 Z 是一名大一的新生，今天 H 老师刚刚在上课的时候讲了插入排序算法。

假设比较两个元素的时间为 O ( 1 ) \mathcal O(1) O(1)，则插入排序可以以 O ( n 2 ) \mathcal O(n^2) O(n2) 的时间复杂度完成长度为 n n n 的数组的排序。不妨假设这 n n n 个数字分别存储在 a 1 , a 2 , … , a n a_1, a_2, \ldots, a_n a1​,a2​,…,an​ 之中，则如下伪代码给出了插入排序算法的一种最简单的实现方式：

这下面是 C/C++ 的示范代码

for (int i = 1; i <= n; i++)
	for (int j = i; j >= 2; j--)
		if (a[j] < a[j-1]) {
     
			int t = a[j-1];
			a[j-1] = a[j];
			a[j] = t;
		}

这下面是 Pascal 的示范代码

for i:=1 to n do
	for j:=i downto 2 do
		if a[j]

为了帮助小 Z 更好的理解插入排序，小 Z 的老师 H 老师留下了这么一道家庭作业：

H 老师给了一个长度为 n n n 的数组 a a a，数组下标从 1 1 1 开始，并且数组中的所有元素均为非负整数。小 Z 需要支持在数组 a a a 上的 Q Q Q 次操作，操作共两种，参数分别如下：

1   x   v 1~x~v 1 x v：这是第一种操作，会将 a a a 的第 x x x 个元素，也就是 a x a_x ax​ 的值，修改为 v v v。保证 1 ≤ x ≤ n 1 \le x \le n 1≤x≤n， 1 ≤ v ≤ 1 0 9 1 \le v \le 10^9 1≤v≤109。注意这种操作会改变数组的元素，修改得到的数组会被保留，也会影响后续的操作。

2   x 2~x 2 x：这是第二种操作，假设 H 老师按照上面的伪代码对 a a a 数组进行排序，你需要告诉 H 老师原来 a a a 的第 x x x 个元素，也就是 a x a_x ax​，在排序后的新数组所处的位置。保证 1 ≤ x ≤ n 1 \le x \le n 1≤x≤n。注意这种操作不会改变数组的元素，排序后的数组不会被保留，也不会影响后续的操作。

H 老师不喜欢过多的修改，所以他保证类型 1 1 1 的操作次数不超过 5000 5000 5000。

小 Z 没有学过计算机竞赛，因此小 Z 并不会做这道题。他找到了你来帮助他解决这个问题。

输入输出格式

输入格式

第一行，包含两个正整数 n , Q n, Q n,Q，表示数组长度和操作次数。
第二行，包含 n n n 个空格分隔的非负整数，其中第 i i i 个非负整数表示 a i a_i ai​。
接下来 Q Q Q 行，每行 2 ∼ 3 2 \sim 3 2∼3 个正整数，表示一次操作，操作格式见【题目描述】。

输出格式

对于每一次类型为 2 2 2 的询问，输出一行一个正整数表示答案。

输入输出样例

输入样例 #1

3 4 3 2 1
2 3
1 3 2
2 2
2 3

输出样例 #1

1
1
2

说明

【样例解释 #1】

在修改操作之前，假设 H 老师进行了一次插入排序，则原序列的三个元素在排序结束后所处的位置分别是 3 , 2 , 1 3, 2, 1 3,2,1。

在修改操作之前，假设 H 老师进行了一次插入排序，则原序列的三个l元素在排序结束后所处的位置分别是 3 , 1 , 2 3, 1, 2 3,1,2。

注意虽然此时 a 2 = a 3 a_2 = a_3 a2​=a3​，但是我们不能将其视为相同的元素。

【样例解释 #2】

见附件中的 sort/sort2.in 与 sort/sort2.ans。

该测试点数据范围同测试点 1 ∼ 2 1 \sim 2 1∼2。

【样例解释 #3】

见附件中的 sort/sort3.in 与 sort/sort3.ans。

该测试点数据范围同测试点 3 ∼ 7 3 \sim 7 3∼7。

【样例解释 #4】

见附件中的 sort/sort4.in 与 sort/sort4.ans。

该测试点数据范围同测试点 12 ∼ 14 12 \sim 14 12∼14。

【数据范围】

对于所有测试数据，满足 1 ≤ n ≤ 8000 1 \le n \le 8000 1≤n≤8000， 1 ≤ Q ≤ 2 × 10 5 1 \le Q \le 2 \times {10}^5 1≤Q≤2×105， 1 ≤ x ≤ n 1 \le x \le n 1≤x≤n， 1 ≤ v , a i ≤ 1 0 9 1 \le v,a_i \le 10^9 1≤v,ai​≤109。

对于所有测试数据，保证在所有 Q Q Q 次操作中，至多有 5000 5000 5000 次操作属于类型一。

各测试点的附加限制及分值如下表所示。

测试点 n ≤ n \le n≤ Q ≤ Q \le Q≤ 特殊性质
1 ∼ 4 1 \sim 4 1∼4 10 10 10 10 10 10 无
5 ∼ 9 5 \sim 9 5∼9 300 300 300 300 300 300 无
10 ∼ 13 10 \sim 13 10∼13 1500 1500 1500 1500 1500 1500 无
14 ∼ 16 14 \sim 16 14∼16 8000 8000 8000 8000 8000 8000 保证所有输入的 a i , v a_i,v ai​,v 互不相同
17 ∼ 19 17 \sim 19 17∼19 8000 8000 8000 8000 8000 8000 无
20 ∼ 22 20 \sim 22 20∼22 8000 8000 8000 2 × 1 0 5 2 \times 10^5 2×105 保证所有输入的 a i , v a_i,v ai​,v 互不相同
23 ∼ 25 23 \sim 25 23∼25 8000 8000 8000 2 × 1 0 5 2 \times 10^5 2×105 无

☀️解题思路

题目大意

给出长度为n的数组与q次操作，每次操作有两种类型：
1️⃣ 将a[x]改为v。
2️⃣ 求出进行插入排序后之前的a[x]排在第几位（不改变数组中元素值）。

36分做法：直接模拟

对于每次修改操作，直接将a[x]赋值为v；
对于每次查询操作，按照题目中给出的插入排序代码排序，求出a[x]的位置。
时间复杂度：O(qn2)，O(1)修改，O(n2)查询
空间复杂度：O(n)

52分做法：快排优化

在36分做法的基础上手写cmp函数（若值不同，值越小越靠前；否则，输入时的下标越小越靠前，模拟插入排序），对于每次查询操作用sort代替插入排序。
时间复杂度：O(qnlogn)，O(1)修改，O(nlogn)查询
空间复杂度：O(n)

76分做法：模拟排序

其实对于每次查询操作，我们并不需要大动干戈地排一遍序，此时：
答案 = x - ∑ i = 1 x − 1 a [ i ] > a [ x ] + ∑ i = x + 1 n a [ i ] < a [ x ] \displaystyle \sum_{i=1}^{x-1} {a[i]>a[x]} +\sum_{i=x+1}^{n} {a[i]i=1∑x−1​a[i]>a[x]+i=x+1∑n​a[i]<a[x]
原理想必大家都懂，就是在最开始x的基础上先向左找不合法的元素然后向左移，再向右找不合法的元素然后向右移，这样遍历一遍就能得出最终a[x]的下标了。
时间复杂度：O(qn)，O(1)修改，O(n)查询。
空间复杂度：O(n)

100分做法1：前后冒泡

小伙伴们可以发现，前几个方法的修改都是直接O(1)，然后再查询上做文章。但是题目中说过，修改最多只有5000次，而查询最多有2 * 105次，所以正解肯定需要一个O(1)的查询。

对于每次修改操作，我们需要让数组有序并且记录下元素的下标，那么问题来了：
在一个有序的数组中插入一个数，如何让数组有序？
既然数组有序，我们可以将新插入的数分为两类：

  1. 应该放在前面的数
  2. 应该放在后面的数

对于1，我们将这段数排一下序就ok了。当然不要浪费前面所有数有序的特性，我们将这段数向前冒泡即可。
对于2，同理，向后冒泡。
时间复杂度：O(qn2)，O(n)修改，O(1)查询。

100分做法2：线段树维护

在修改查询这类题中线段树是肥肠常用的算法啦~
幸运的是插入排序是稳定排序，但是线段树不能插入两个量（值和下标）鸭。
所以这里我们用一个权值表现这两个量：n * a[i] + i - 1。
接下来就是上模板了。
对于不会的小伙伴们蒟蒻君在这里也不细讲了 （毕竟能力时间有限），麻烦出门右转百度~
由于线段树处理1 ~ 2n，导致修改查询复杂度是常数级的。
时间复杂度：O(q)，修改O(1)，查询O(1)（63次）。
空间复杂度：O(n)。

☀️代码实现

36分做法：直接模拟

#include 
using namespace std;
const int N = 8005;
// b: 用来给a排序
// c[i]: a[i]在b中的位置 
// d[i]: b[i]在a中的位置 
int a[N], b[N], c[N], d[N];
int main() {
     
    int n, q;
    cin >> n >> q;
    for (int i = 1; i <= n; ++i) {
     
    	cin >> a[i];
    }
    while (q--) {
     
        int op;
        cin >> op;
        if (op == 1) {
     
            int x, v;
            cin >> x >> v;
            a[x] = v;
        } else {
     
            int x;
            cin >> x;
            for (int i = 1; i <= n; ++i) {
     
            	b[i] = a[i];
            	c[i] = d[i] = i;
			}
			for (int i = 1; i <= n; ++i) {
     
				for (int j = i; j >= 2; --j) {
     
					if (b[j] < b[j - 1]) {
     
						swap(b[j], b[j - 1]);
						c[d[j]] = j - 1;
						c[d[j - 1]] = j;
						swap(d[j], d[j - 1]);
					}
				}
			}
			cout << c[x] << '\n';
        }
    }
    return 0;
}

52分做法：快排优化

#include 
using namespace std;
struct node {
     
	int num, id;
} a[8005], b[8005];
inline bool cmp(node x, node y) {
     
	if (x.num != y.num) {
     
		return x.num < y.num;
	}
	return x.id < y.id;
}
int main() {
     
	int n, q;
	cin >> n >> q;
	for (int i = 1; i <= n; ++i) {
     
		cin >> a[i].num;
		a[i].id = i;
	}
	while (q--) {
     
		int op;
		cin >> op;
		if (op == 1) {
     
			int x, v;
			cin >> x >> v;
			a[x].num = v;
		} else {
     
			int x;
			cin >> x;
			for (int i = 1; i <= n; ++i) {
     
				b[i] = a[i];
			}
			sort(b + 1, b + n + 1, cmp);
			for (int i = 1; i <= n; ++i) {
     
				if (b[i].id == x) {
     
					cout << i << '\n';
					break;
				}
			}
		}
	}
	return 0;
}

76分做法：模拟排序

#include 
using namespace std;
int a[8005];
int main() {
     
	int n, q;
	cin >> n >> q;
	for (int i = 1; i <= n; ++i) {
     
		cin >> a[i];
	}
	while (q--) {
     
		int op;
		cin >> op;
		if (op == 1) {
     
			int x, v;
			cin >> x >> v;
			a[x] = v;
		} else {
     
			int x;
			cin >> x;
			int res = x;
			for (int i = 1; i < x; ++i) {
     
				res -= (a[i] > a[x]);
			}
			for (int i = x + 1; i <= n; ++i) {
     
				res += (a[i] < a[x]);
			}
			cout << res << '\n';
		}
	}
    return 0;
}

100分做法1：前后冒泡

#include 
using namespace std;
const int N = 8005;
struct node {
     
    int num, id;
} a[N];
inline bool cmp(node x, node y) {
     
    if (x.num != y.num) {
     
        return x.num < y.num;
    }
    return x.id < y.id;
}
int b[N];
int main() {
     
    int n, q;
    cin >> n >> q;
    for (int i = 1; i <= n; ++i) {
     
        cin >> a[i].num;
        a[i].id = i;
    }
    sort(a + 1, a + n + 1, cmp);
    for (int i = 1; i <= n; ++i) {
     
        b[a[i].id] = i;
    }
    while (q--) {
     
        int op;
        cin >> op;
        if (op == 1) {
     
            int x, v;
            cin >> x >> v;
            int k = b[x];
            a[k].num = v;
            while (!cmp(a[k - 1], a[k]) && k > 1) {
     
                swap(a[k - 1], a[k]);
                --k;
            }
            while (!cmp(a[k], a[k + 1]) && k < n) {
     
                swap(a[k], a[k + 1]);
                ++k;
            }
            for (int i = 1; i <= n; ++i) {
     
                b[a[i].id] = i;
            }
        } else {
     
            int x;
            cin >> x;
            cout << b[x] << '\n';
        }
    }
    return 0;
}

100分做法2：线段树维护

温馨提示： 若cin/cout不加去同步优化会T掉6个点，退化成76分算法。

#include 
using namespace std;
typedef long long ll;
ll a[8005];
struct node {
     
	int son[2], vis;
} t[5000005];
int k = 1;
void add(ll x) {
     
	int p = 1;
	++t[p].vis;
	for (int i = 63; i >= 0; --i) {
     
		bool b = (x >> i) & 1;
		if (!t[p].son[b]) {
     
			t[p].son[b] = ++k;
        }
		p = t[p].son[b];
		++t[p].vis;
	}
}
void move(ll x) {
     
	int p = 1;
	--t[p].vis;
	for (int i = 63; i >= 0; --i) {
     
		p = t[p].son[(x >> i) & 1];
		if (!p) {
     
            return ;
        }
		--t[p].vis;
	}
}
int query(ll x) {
     
	int res = 0, p = 1;
	for (int i = 63; i >= 0; --i) {
     
		bool b = (x >> i) & 1;
		if (b) {
     
            res += t[t[p].son[0]].vis;
        }
		p = t[p].son[b];
		if (!p) {
     
            return res;
        }
	}
	return res;
}
int main() {
     
    ios :: sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
	int n, q;
    cin >> n >> q;
	for (int i = 1; i <= n; ++i) {
     
        cin >> a[i];
		add(1ll * (a[i] * n + i - 1));
	}
	for (int i = 1; i <= q; ++i) {
     
        int op;
		cin >> op;
		if (op == 1) {
     
            int x, v;
			cin >> x >> v;
			move(1ll * (a[x] * n + x - 1));
			a[x] = v;
			add(1ll * (a[x] * n + x - 1));
		} else {
     
            int x;
            cin >> x;
            cout << query(1ll * (a[x] * n + x - 1) + 1) << '\n';
        }
	}
	return 0;
}

CSPJ2021考完了，你，AK了吗？_第4张图片

T3： 网络连接

☀️题目信息

题目描述

TCP/IP 协议是网络通信领域的一项重要协议。今天你的任务，就是尝试利用这个协议，还原一个简化后的网络连接场景。

在本问题中，计算机分为两大类：服务机（Server）和客户机（Client）。服务机负责建立连接，客户机负责加入连接。

需要进行网络连接的计算机共有 n n n 台，编号为 1 ∼ n 1 \sim n 1∼n，这些机器将按编号递增的顺序，依次发起一条建立连接或加入连接的操作。

每台机器在尝试建立或加入连接时需要提供一个地址串。服务机提供的地址串表示它尝试建立连接的地址，客户机提供的地址串表示它尝试加入连接的地址。

一个符合规范的地址串应当具有以下特征：

  1. 必须形如 a.b.c.d:e 的格式，其中 a , b , c , d , e a, b, c, d, e a,b,c,d,e 均为非负整数；
  2. 0 ≤ a , b , c , d ≤ 255 0 \le a, b, c, d \le 255 0≤a,b,c,d≤255， 0 ≤ e ≤ 65535 0 \le e \le 65535 0≤e≤65535；
  3. a , b , c , d , e a, b, c, d, e a,b,c,d,e 均不能含有多余的前导 0 0 0。

相应地，不符合规范的地址串可能具有以下特征：

  1. 不是形如 a.b.c.d:e 格式的字符串，例如含有多于 3 3 3 个字符 . 或多于 1 1 1 个字符 : 等情况；
  2. 整数 a , b , c , d , e a, b, c, d, e a,b,c,d,e 中某一个或多个超出上述范围；
  3. 整数 a , b , c , d , e a, b, c, d, e a,b,c,d,e 中某一个或多个含有多余的前导 0 0 0。

例如，地址串 192.168.0.255:80 是符合规范的，但 192.168.0.999:80、192.168.00.1:10、192.168.0.1:088、192:168:0:1.233 均是不符合规范的。

如果服务机或客户机在发起操作时提供的地址串不符合规范，这条操作将被直接忽略。

在本问题中，我们假定凡是符合上述规范的地址串均可参与正常的连接，你无需考虑每个地址串的实际意义。

由于网络阻塞等原因，不允许两台服务机使用相同的地址串，如果此类现象发生，后一台尝试建立连接的服务机将会无法成功建立连接；除此之外，凡是提供符合规范的地址串的服务机均可成功建立连接。

如果某台提供符合规范的地址的客户机在尝试加入连接时，与先前某台已经成功建立连接的服务机提供的地址串相同，这台客户机就可以成功加入连接，并称其连接到这台服务机；如果找不到这样的服务机，则认为这台客户机无法成功加入连接。

请注意，尽管不允许两台不同的服务机使用相同的地址串，但多台客户机使用同样的地址串，以及同一台服务机同时被多台客户机连接的情况是被允许的。

你的任务很简单：在给出每台计算机的类型以及地址串之后，判断这台计算机的连接情况。

输入输出格式

输入格式

第一行，一个正整数 $n$。

接下来 n n n 行，每行两个字符串 o p , a d \mathit{op}, \mathit{ad} op,ad，按照编号从小到大给出每台计算机的类型及地址串。

其中 o p \mathit{op} op 保证为字符串 Server 或 Client 之一， a d \mathit{ad} ad 为一个长度不超过 25 25 25 的，仅由数字、字符 . 和字符 : 组成的非空字符串。

每行的两个字符串之间用恰好一个空格分隔开，每行的末尾没有多余的空格。

输出格式

输出共 n n n 行，每行一个正整数或字符串表示第 i i i 台计算机的连接状态。其中：

如果第 i i i 台计算机为服务机，则：

  1. 如果其提供符合规范的地址串且成功建立连接，输出字符串 OK。
  2. 如果其提供符合规范的地址串，但由于先前有相同地址串的服务机而无法成功建立连接，输出字符串 FAIL。
  3. 如果其提供的地址串不是符合规范的地址串，输出字符串 ERR。

如果第 i i i 台计算机为客户机，则：

  1. 如果其提供符合规范的地址串且成功加入连接，输出一个正整数表示这台客户机连接到的服务机的编号。
  2. 如果其提供符合规范的地址串，但无法成功加入连接时，输出字符串 FAIL。
  3. 如果其提供的地址串不是符合规范的地址串，输出字符串 ERR。

输入输出样例

输入样例 #1

5
Server 192.168.1.1:8080
Server 192.168.1.1:8080
Client 192.168.1.1:8080
Client 192.168.1.1:80
Client 192.168.1.1:99999

输出样例 #1

OK
FAIL
1
FAIL
ERR

输入样例 #2

10
Server 192.168.1.1:80
Client 192.168.1.1:80
Client 192.168.1.1:8080
Server 192.168.1.1:80
Server 192.168.1.1:8080
Server 192.168.1.999:0
Client 192.168.1.1.8080
Client 192.168.1.1:8080
Client 192.168.1.1:80
Client 192.168.1.999:0

输出样例 #2

OK
1
FAIL
FAIL
OK
ERR
ERR
5
1
ERR

输入样例 #3

见附件中的 network/network3.in。

输出样例 #3

见附件中的 network/network3.ans。

输入样例 #4

见附件中的 network/network4.in。

输出样例 #4

见附件中的 network/network4.ans。

说明

【样例解释 #1】

计算机 1 1 1 为服务机，提供符合规范的地址串 192.168.1.1:8080，成功建立连接；

计算机 2 2 2 为服务机，提供与计算机 1 1 1 相同的地址串，未能成功建立连接；

计算机 3 3 3 为客户机，提供符合规范的地址串 192.168.1.1:8080，成功加入连接，并连接到服务机 1 1 1；

计算机 4 4 4 为客户机，提供符合规范的地址串 192.168.1.1:80，找不到服务机与其连接；

计算机 5 5 5 为客户机，提供的地址串 192.168.1.1:99999 不符合规范。

【数据范围】

测试点编号 n ≤ n \le n≤ 特殊性质
1 1 1 10 10 10 性质 1 2 3
2 ∼ 3 2 \sim 3 2∼3 100 100 100 性质 1 2 3
4 ∼ 5 4 \sim 5 4∼5 1000 1000 1000 性质 1 2 3
6 ∼ 8 6 \sim 8 6∼8 1000 1000 1000 性质 1 2
9 ∼ 11 9 \sim 11 9∼11 1000 1000 1000 性质 1
12 ∼ 13 12 \sim 13 12∼13 1000 1000 1000 性质 2
14 ∼ 15 14 \sim 15 14∼15 1000 1000 1000 性质 4
16 ∼ 17 16 \sim 17 16∼17 1000 1000 1000 性质 5
18 ∼ 20 18 \sim 20 18∼20 1000 1000 1000 无特殊性质

“性质 1”为：保证所有的地址串均符合规范；
“性质 2”为：保证对于任意两台不同的计算机，如果它们同为服务机或者同为客户机，则它们提供的地址串一定不同；
“性质 3”为：保证任意一台服务机的编号都小于所有的客户机；
“性质 4”为：保证所有的地址串均形如 a.b.c.d:e 的格式，其中 a , b , c , d , e a, b, c, d, e a,b,c,d,e 均为不超过 10 9 {10}^9 109 且不含有多余前导 0 0 0 的非负整数；
“性质 5”为：保证所有的地址串均形如 a.b.c.d:e 的格式，其中 a , b , c , d , e a, b, c, d, e a,b,c,d,e 均为只含有数字的非空字符串。

对于 100 % 100 \% 100% 的数据，保证 1 ≤ n ≤ 1000 1 \le n \le 1000 1≤n≤1000。

☀️解题思路

这题的名字好像图论哦

题目大意

给出n台计算机的地址串，每台计算机都是服务机或者客户机。
若地址串不合法，输出"ERR"，否则：

  • 若计算机为服务机，判断此地址串是否出现过。若出现过输出"FAIL"，否则输出"OK"。
  • 若计算机为客户机，若出现过此地址串的客户机，输出这台客户机是第几台（即第几个输出的），否则输出"FAIL"。

思路分析：大模拟

思路应该比较简单，这道题主要有两个难点：

  1. 如何判断一个地址串是否合法？
  2. 如何判断一个地址串是否之前出现过，若出现过是第几个出现的？

对于第一个问题，我们直接按题目中所说的规则去模拟就好了，对于第二个问题其实我们用STL里的map就行了（蒟蒻君的方法不一定是最好用的）。
这里我们可以定义一个映射表：

  • 第一维是string类型的，就是我们的地址串；
  • 第二维是int类型的，代表此地址串在第几台计算机中出现了。

易错点

（位置在代码中注释易错点1,2的地方）

易错点1

注意判断3个’.‘和’:‘的顺序，即’:‘是否在’.'的前面，若没有判断就是可怜的75pts。

易错点2

注意题目中说的没有前导0，不能只判断a,b,c,d,e的第一位是不是0，若a,b,c,d,e==0，判断错误，可怜的10pts。

☀️代码实现

#include 
using namespace std;
typedef long long ll;
// 将字符串s转化成int类型
ll to_int(string s) {
     
	ll res = 0, base = 1;
	int n = (int)s.size();
	for (int i = n - 1; i >= 0; --i) {
     
		res += base * (s[i] - '0');
		base *= 10;
	}
	return res;
}
// 判断s作为地址串是否合法
bool check(string s) {
     
	// n: s的长度
	// cnt1: '.'的个数
	// cnt2: ':'的个数
	int n = (int)s.size(), cnt1 = 0, cnt2 = 0;
	for (int i = 0; i < n; ++i) {
     
		if (s[i] == '.') {
     
			++cnt1;
			continue;
		}
		if (s[i] == ':') {
     
			++cnt2;
			continue;
		}
		// 若地址串的这一位既不是数字，又不是'.'和':'，地址串非法
		if (s[i] < '0' || s[i] > '9') {
     
			return false;
		}
	}
	// 若'.'的数量不是3个或':'的数量不是1个，地址串非法
	if (cnt1 != 3 || cnt2 != 1) {
     
		return false;
	}
	// pos[i] (0 ≤ i ≤ 3): 第(i + 1)个'.'的位置
	// pos[4]: ':'的位置
	int pos[4], k = 0;
	for (int i = 0; i < n; ++i) {
     
		// 易错点1
		if (s[i] == ':' && k != 3) {
     
			return false;
		}
		if (s[i] == '.' || s[i] == ':') {
     
			pos[k++] = i;
		}
	}
	for (int i = 0; i < 3; ++i) {
     
		if (pos[i] + 1 == pos[i + 1]) {
     
			return false;
		}
	}
	ll a = to_int(s.substr(0, pos[0]));
	ll b = to_int(s.substr(pos[0] + 1, pos[1] - pos[0] - 1));
	ll c = to_int(s.substr(pos[1] + 1, pos[2] - pos[1] - 1));
	ll d = to_int(s.substr(pos[2] + 1, pos[3] - pos[2] - 1));
	ll e = to_int(s.substr(pos[3] + 1, n - 1 - pos[3]));
	// 若a~e范围非法，地址串非法
	if (a > 255 || b > 255 || c > 255 || d > 255 || e > 65535) {
     
		return false;
	}
	// 易错点2
	if ((a != 0 && s[0] == '0') || (b != 0 && s[pos[0] + 1] == '0') || (c != 0 && s[pos[1] + 1] == '0') || (d != 0 && s[pos[2] + 1] == '0') || (e != 0 && s[pos[3] + 1] == '0')) {
     
		return false;
	}
	return true;
}
map<string, int> mp;
int main() {
     
	ios :: sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int n;
	cin >> n;
	for (int i = 1; i <= n; ++i) {
     
		string op, s;
		cin >> op >> s;
		if (check(s) == false) {
     
			cout << "ERR\n";
			continue;
		}
		if (op[0] == 'S') {
     
			if (mp.count(s)) {
     
				cout << "FAIL\n";
			} else {
     
				// value_type: 相当于是pair里面的make_pair，将(s, i)转化成map的形式
				mp.insert(map<string, int> :: value_type(s, i));
				cout << "OK\n";
			}
		} else {
     
			if (mp.count(s)) {
     
				cout << mp[s] << '\n';
			} else {
     
				cout << "FAIL\n";
			}
		}
	}
	return 0;
}

T4：小熊的果篮

☀️题目信息

题目描述

小熊的水果店里摆放着一排 n n n 个水果。每个水果只可能是苹果或桔子，从左到右依次用正整数 1 , 2 , … , n 1, 2, \ldots, n 1,2,…,n 编号。连续排在一起的同一种水果称为一个“块”。小熊要把这一排水果挑到若干个果篮里，具体方法是：每次都把每一个“块”中最左边的水果同时挑出，组成一个果篮。重复这一操作，直至水果用完。注意，每次挑完一个果篮后，“块”可能会发生变化。比如两个苹果“块”之间的唯一桔子被挑走后，两个苹果“块”就变成了一个“块”。请帮小熊计算每个果篮里包含的水果。

输入输出格式

输入格式

第一行，包含一个正整数 n n n，表示水果的数量。
第二行，包含 n n n 个空格分隔的整数，其中第 i i i 个数表示编号为 i i i 的水果的种类， 1 1 1 代表苹果， 0 0 0 代表桔子。

输出格式

输出若干行。
第 i i i 行表示第 i i i 次挑出的水果组成的果篮。从小到大排序输出该果篮中所有水果的编号，每两个编号之间用一个空格分隔。

输入输出样例

输入样例 #1

12
1 1 0 0 1 1 1 0 1 1 0 0

输出样例 #1

1 3 5 8 9 11
2 4 6 12
7
10

输入样例 #2

20
1 1 1 1 0 0 0 1 1 1 0 0 1 0 1 1 0 0 0 0

输出样例 #2

1 5 8 11 13 14 15 17
2 6 9 12 16 18
3 7 10 19
4 20

输入样例 #3

见附件中的 fruit/fruit3.in。

输出样例 #3

见附件中的 fruit/fruit3.ans。

说明

【样例解释 #1】

这是第一组数据的样例说明。

所有水果一开始的情况是 [ 1 , 1 , 0 , 0 , 1 , 1 , 1 , 0 , 1 , 1 , 0 , 0 ] [1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0] [1,1,0,0,1,1,1,0,1,1,0,0]，一共有 6 6 6 个块。

在第一次挑水果组成果篮的过程中，编号为 1 , 3 , 5 , 8 , 9 , 11 1, 3, 5, 8, 9, 11 1,3,5,8,9,11 的水果被挑了出来。

之后剩下的水果是 [ 1 , 0 , 1 , 1 , 1 , 0 ] [1, 0, 1, 1, 1, 0] [1,0,1,1,1,0]，一共 4 4 4 个块。

在第二次挑水果组成果篮的过程中，编号为 2 , 4 , 6 , 12 2, 4, 6, 12 2,4,6,12 的水果被挑了出来。

之后剩下的水果是 [ 1 , 1 ] [1, 1] [1,1]，只有 1 1 1 个块。

在第三次挑水果组成果篮的过程中，编号为 7 7 7 的水果被挑了出来。

最后剩下的水果是 [ 1 ] [1] [1]，只有 1 1 1 个块。

在第四次挑水果组成果篮的过程中，编号为 10 10 10 的水果被挑了出来。

【数据范围】

对于 10 % 10 \% 10% 的数据， n ≤ 5 n \le 5 n≤5。
对于 30 % 30 \% 30% 的数据， n ≤ 1000 n \le 1000 n≤1000。
对于 70 % 70 \% 70% 的数据， n ≤ 50000 n \le 50000 n≤50000。
对于 100 % 100 \% 100% 的数据， 1 ≤ n ≤ 2 × 10 5 1 \le n \le 2 \times {10}^5 1≤n≤2×105。

【提示】

由于数据规模较大，建议 C/C++ 选手使用 scanf 和 printf 语句输入、输出。

☀️解题思路

题目大意

给出一个长度为n的数组，每一位必为0或1，连续的一段0或1被称为1个“块”，每次输出所有“块”的第一位的编号，被输出的位直接删除。
注意每轮输出后，所有的“块”都是“重新组合”的，如：

12
1 1 0 0 1 1 1 0 1 1 0 0

第一轮：
CSPJ2021考完了，你，AK了吗？_第5张图片
第二轮：
CSPJ2021考完了，你，AK了吗？_第6张图片

70分做法：模拟

按照题目说的意思直接模拟，代码细节较多。
时间复杂度：O(n2)
空间复杂度：O(n)

100分做法1：队列维护+模拟

用队列维护每一个“块”，若两个块在队列里相邻且元素相同，直接合并，代码细节还是有亿点多。
时间复杂度：O(nlogn)
空间复杂度：O(n)

100分做法2：珂朵莉树

看大佬的题解说这题就是个珂朵莉树模板 （可惜我太弱了根本布吉岛珂朵莉树是啥）。
时间复杂度：O(nlogn)
空间复杂度：O(n)

☀️代码实现

70分做法：模拟

#include 
using namespace std;
struct node {
     
	bool num;
	int id;
} a[200005];
int main() {
     
	int n;
	cin >> n;
	for (int i = 1; i <= n; ++i) {
     
		cin >> a[i].num;
		a[i].id = i;
	}
	while (n >= 1) {
     
		vector<int> b;
		for (int i = 1; i <= n; ++i) {
     
			if (a[i].num == a[i - 1].num && i != 1) {
     
				continue;
			}
			cout << a[i].id << ' ';
			b.push_back(i);
		}
		for (int i = 0; i < (int)b.size(); ++i) {
     
			for (int j = b[i]; j < n; ++j) {
     
				a[j] = a[j + 1];
			}
			for (int j = i + 1; j < (int)b.size(); ++j) {
     
				--b[j];
			}
			--n;
		}
		cout << '\n';
	}
	return 0;
}

100分做法：队列维护+模拟

#include 
using namespace std;
const int N = 200005;
int a[N], b[N], c[N], id[N];
bool flag[N];
int main() {
     
    int n;
	cin >> n;
	for (int i = 1; i <= n; ++i) {
     
        cin >> a[i];
    }
	a[0] = a[n + 1] = INT_MAX;
	for (int i = 1; i <= n; ++i) {
     
        b[i] = i - 1;
        c[i] = i + 1;
    }
    int k = 0;
	id[++k] = 1;
	for (int i = 2; i <= n; ++i) {
     
        if (a[i] != a[i - 1]) {
     
            id[++k] = i;
        }
    }
	while (k) {
     
		for (int i = 1; i <= k; ++i) {
     
            cout << id[i] << ' ';
        }
        cout << '\n';
		int cnt = 0;
		for (int i = 1; i <= k; ++i) {
     
			c[b[id[i]]] = c[id[i]];
			b[c[id[i]]] = b[id[i]];
			if (a[c[id[i]]] == a[id[i]] && a[b[id[i]]] != a[id[i]]) {
     
                id[++cnt] = c[id[i]];
            }
		}
		k = cnt;
	}
	return 0;
}

100分做法2：珂朵莉树

这里直接照搬代码。

// Author : Luogu Canstant0x5F3759DF
#include 
#define lld long long
using namespace std;
#define frein(x) freopen(x, "r", stdin)
#define freout(x) freopen(x, "w", stdout)
struct seg {
     
	int l, r;
};
bool operator < (const seg & a, const seg & b) {
     
	return a.r < b.r;
}
set<seg> s;
int n;
int a[300010];
bool del[300010];
void remove(set<seg>::iterator & it) {
     
	seg x = *it;
	if (!x.l || !x.r) return;
	s.erase(it ++);
	del[x.l] = 1;
	++ x.l;
	while (del[x.l] && x.l <= x.r) ++ x.l;
	if (x.r < x.l) return;
	if (it != s.begin()) {
     
		set<seg>::iterator jt = it;
		-- jt;
		if (a[jt->r] == a[x.l]) {
     
			seg t = *jt;
			s.erase(jt);
			t.r = x.r;
			s.insert(t);
			return;
		}
	}
	s.insert(x);
}
int main() {
     
	scanf("%d", &n);
	a[0] = -1;
	seg x;
	x.l = x.r = 0;
	for (int i = 1; i <= n; ++ i) {
     
		scanf("%d", a + i);
		if (a[i] == a[i - 1]) x.r  = i;
		else {
     
			if (x.l) s.insert(x);
			x.l = x.r = i;
		}
	}
 	s.insert(x);
	set<seg>::iterator it;
	while (s.size()) {
     
		for (it = s.begin(); it != s.end(); ++ it) 
			printf("%d ", it->l);
		puts("");
		for (it = s.begin(); it != s.end();)
			remove(it);
	}
	return 0;
}

附件下载

（我打死也不会告诉你我不会弄超链接下载）
考虑到文章长度问题，蒟蒻君把附件上传到了洛谷剪切板。
⭐T1~T2点击这里⭐
⭐T3~T4点击这里⭐
CSPJ2021考完了，你，AK了吗？_第7张图片

你可能感兴趣的:(算法,NOIP题解,C++,NOIP/CSP,算法,题解,rp++)

  • C++设计模式---迭代器模式 xinruoqianqiu 设计模式设计模式迭代器模式
    1、介绍迭代器模式是⼀种行为型设计模式，是⼀种使⽤频率⾮常⾼的设计模式，在各个语⾔中都有应用，其主要⽬的是提供⼀种统⼀的⽅式来访问⼀个聚合对象中的各个元素，而不需要暴露该对象的内部表示。通过迭代器，客户端可以顺序访问聚合对象的元素，而无需了解底层数据结构。迭代器模式应⽤⼴泛，但是⼤多数语⾔都已经内置了迭代器接⼝，不需要⾃⼰实现。包含一下几个部分：（1）迭代器接口Iterator：定义访问和遍历元素
  • 数据结构---C++版 海狸_hlz 数据结构数据结构
    第1章数据结构的基本概念1.1数据结构在程序设计中的作用1）程序设计的实质是什么?数据表示：将数据存储在计算机（内存）中数据处理：处理数据，设计方案（算法）1.2计算机求解问题:1）问题→抽象出问题的模型→求模型的解问题——数值问题、非数值问题2）数值问题→数学方程非数值问题→数据结构3）本书讨论非数值问题的数据组织和处理，主要内容如下：（1）数据的逻辑结构：线性表、树、图等数据结构，其核心是如何
  • 数电票介绍及如何由数电票生成OFD文件 源之缘-OFD解决方案之道 ofd数电票
    本人用c#、c++、typescript分别开发了数电票生成系统，可以生成ofd、pdf、图格式的数电票。采用微服务部署，方便调用！本文主要介绍一下数电票概念及生成过程。1.数电票的概念与特点数电票，即数字电子发票，是指以电子形式生成、传输和存储的发票。它完全取代了传统的纸质发票，具有与纸质发票同等的法律效力。数电票的推广和应用是税务数字化的重要一步，旨在提高开票效率、降低企业成本、减少资源浪费，
  • PCL点云处理算法汇总（C++长期更新低价精品版） 点云侠' 点云学习算法c++开发语言计算机视觉
    可笑，我当然知道是抄袭的啊，还用你提醒？要不是你们审核不作为，我能抄这么明目张胆？？？目录一、点云滤波1、常用滤波器2、采样滤波3、裁剪滤波二、KD树与八叉树1、KD树2、八叉树三、点云配准粗配准精配准对应关系配准精度坐标转换刚体运动变换四、点云拟合分割1、RANSAC2、其他几何分割五、三维重建六、特征点与特征描述1、点云的属性2、关键点提取3、特征描述子七、基础函数1、common模块2、其他
  • Qt C++设计模式-＞中介者模式 多喝热水-多读书 c++设计模式中介者模式qt
    中介者模式（MediatorPattern）是一种行为型设计模式，定义了一个对象用于封装一系列对象之间的交互。中介者使得对象之间不再需要显式地相互引用，减少了对象之间的依赖关系，从而使系统更加松散耦合，并且可以独立地改变对象之间的交互。中介者模式的应用场景中介者模式适用于当多个对象之间存在复杂的通信关系时，通过引入一个中介者对象来管理这些对象之间的交互，避免了对象之间直接相互依赖，降低系统的复杂性
  • C++设计模式--中介者模式 爱学习的蓝调 C++设计模式设计模式中介者模式C++
    中介者模式（MediatorPattern）定义用一个中介对象来封装一系列的对象交互。中介者使各对象不需要显式地相互引用，从而使其耦合松散，而且可以独立地改变它们之间的交互。Mediator：中介者，它定义了一个接口用于与各个Colleague对象通信；ConcreteMediator：具体的中介者，它通过协调各Colleague对象实现协作行为；并了解和维护它的各个Colleague；Colle
  • 深入理解观察者模式 —— Qt信号槽机制的实现 拾工 软件设计观察者模式qt开发语言
    观察者模式是一种行为型设计模式，允许一个对象（被观察者）状态发生变化时通知一组依赖它的对象（观察者），从而实现对象之间的解耦。在这篇文章中，我们将探讨如何用C++和Python实现观察者模式，并在代码中清晰地体现这一设计模式的核心思想。其实Qt的信号槽机制，就是借住了这一设计模式，并对其进行了一些扩展。由于Qt广泛的被C++和Python用户使用，所以这里给出Python和C++两个版本的简单实现
  • C++ 中的异常处理机制是怎样的？什么情况下应该使用异常处理？异常处理的优缺点是什么？ SUN_Gyq javac++jvm
    1)C++中的异常处理机制是怎样的？异常是一种处理错误的方式，当一个函数发现自己无法处理的错误时就可以抛出异常，让函数的直接或间接的调用者处理这个错误throw:当问题出现时，程序会抛出一个异常。这是通过使用throw关键字来完成的。catch:在您想要处理问题的地方，通过异常处理程序捕获异常，catch关键字用于捕获异常，可以有多个catch进行捕获。try:try块中的代码标识将被激活的特定异
  • C/C++ 中有哪些类型转换方式？ 分别有什么区别？类型转换可能会带来哪些问题？ SUN_Gyq javajvm开发语言c++
    1）C/C++中有哪些类型转换方式？分别有什么区别？在C/C++中，常见的类型转换方式有以下几种：隐式类型转换定义：也称为自动类型转换，是由编译器自动完成的类型转换，不需要程序员显式地进行操作。这种转换通常发生在不同数据类型的操作数进行混合运算时，编译器会自动将操作数转换为一种公共类型，然后再进行运算。inta=5;doubleb=3.14;doubleresult=a+b;//在这里，整数a会被
  • 什么是结构体？什么是联合体？结构体和联合体有什么区别？能否在声明过程当中缺省名字？结构体可以包含函数吗？在 C 和 C++ 中有何不同？ SUN_Gyq c语言c++开发语言
    1）结构体结构体（structure）是一种由不同数据类型的成员组成的数据集合类型，它允许将多个相关的变量组合在一起，形成一个更复杂的数据类型。1.找成员当中最大的类型作为对齐2.按照定义的顺序实现空间分配3.实现地址分配要整数倍对齐4.当结构体当中成员为数组时需要将数组拆分成多个该类型的变量5.当结构体当中包含其他结构体类型的结构时先找到它的对齐数从而确定结构体的对齐数再进行分配位域（不存在地址
  • C++设计模式——Iterator迭代器模式 程序员与背包客_CoderZ C/C++设计模式c++设计模式迭代器模式开发语言c语言linux
    一，迭代器模式的定义迭代器模式是一种行为型设计模式，它使得遍历一个容器对象中的元素变得更加简单。迭代器模式将遍历操作从容器对象（如集合、列表）中分离出来，它通过迭代器对象来遍历容器对象中的元素，使得遍历操作与容器对象解耦。迭代器模式可以解决的需求场景是当容器对象内部的结构经常被改变时，需要对外部屏蔽其变化过程。迭代器模式对外提供了一个统一的遍历接口，这个接口可以顺序访问容器对象中的每个元素。迭代器
  • C++实现设计模式---中介者模式 (Mediator) 计算机小混子 设计模式c++设计模式中介者模式
    中介者模式(Mediator)中介者模式是一种行为型设计模式，它用一个中介对象来封装一组对象之间的交互。中介者通过协调多个对象之间的通信，避免对象之间的直接依赖，从而实现对象之间的松耦合。意图通过引入一个中介者对象，减少对象之间的直接依赖，从而降低耦合性。中介者负责管理和协调对象之间的通信。使用场景对象之间的交互变得复杂：如果对象之间存在大量的直接引用和交互，可以使用中介者模式减少耦合。希望解耦多
  • C++实现设计模式---迭代器模式 (Iterator) 计算机小混子 设计模式c++设计模式迭代器模式
    迭代器模式(Iterator)迭代器模式是一种行为型设计模式，它提供了一种方法，顺序访问一个聚合对象中的各个元素，而又不需要暴露该对象的内部表示。意图提供一种方法，可以顺序访问一个容器对象中的元素，而无需暴露其内部实现。将遍历行为从集合对象中分离出来，使得遍历行为可以独立变化。使用场景需要顺序访问一个聚合对象中的元素：如数组、链表或集合。需要支持多种遍历方式：如正序遍历、反序遍历等。需要解耦遍历算
  • 【YOLOv8杂草作物目标检测】 stsdddd YOLO目标检测目标检测YOLO目标检测人工智能
    YOLOv8杂草目标检测算法介绍模型和数据集下载算法介绍YOLOv8在禾本科杂草目标检测方面有显著的应用和效果。以下是一些关键信息的总结：农作物幼苗与杂草检测系统：基于YOLOv8深度学习框架，通过2822张图片训练了一个目标检测模型，用于检测田间的农作物幼苗与杂草对象。该系统支持图片、视频以及摄像头进行目标检测，并能保存检测结果。系统界面可实时显示目标位置、目标总数、置信度、用时等信息。YOLO
  • c++如何输出质数 z5z3c c++算法
    以输出1到100之间的质数为例方法一//打印数组voidprint(vector&v){for(vector::iteratorit=v.begin();it!=v.end();it++){coutv;v.clear();for(inti=2;i&v){for(vector::iteratorit=v.begin();it!=v.end();it++){coutv;v.clear();//因为遍历
  • Nginx 集群测试 小馋喵知识杂货铺 性能中间件
    在Nginx集群的部署和维护过程中，为了确保系统的高可用性、性能和扩展性，必须进行全面的测试。以下是Nginx集群需要进行的几类主要测试：1.集群有效性测试集群有效性测试的主要目的是验证Nginx集群的基本功能是否正常工作，确保流量分发和负载均衡按预期运行。测试内容：负载均衡验证：确保Nginx按照配置的负载均衡算法（如轮询、加权轮询、IP哈希等）正确地分发请求。测试方法：使用压力测试工具模拟请求
  • Qt开发技术【C++ 实现类的二进制序列化与反序列化】 增援未来章北海 QTC++学习qtc++数据库
    一、思考Qt本身的QByteArray和QDataStreamQDataStream和QByteArray是Qt框架中用于数据序列化和反序列化的类。QDataStream可以将Qt数据类型（如QString、QByteArray等）序列化为二进制格式，并写入文件或网络流中。同时，也可以从文件或网络流中读取二进制数据并反序列化成相应的数据类型。但是在嵌入式中使用代码比较冗余二、实现一个比较简单的仅对
  • 【视觉算法—视频目标跟踪】基于camshift实现视频目标实时追踪 明月下 视觉算法opencvpython音视频
    本文代码功能：1.获取摄像头，实时显示2.鼠标获取第一帧中的目标roi区域3.在视频中实时对目标进行追踪。4.两种目标追踪的方式：‘meanshift’，‘camshift’5.保存视频代码准备新建test.py，复制以下代码：importcv2ascvimportnumpyasnpglobalmin_y,height,min_x,width#1代表打开外置摄像头,外置多个摄像头可依此枚举0，1，
  • 【国内直连】国内可用的ChatGPT中文版镜像集合（2025年1月更新）
    更新时间：2025年01月18日全方位指南，带您轻松使用ChatGPT中文版，支持GPT-4，无需！本文提供详细的ChatGPT中文版使用说明，包括镜像站推荐、官网注册教程以及常见问题解答，帮助您快速掌握ChatGPT的使用方法。目录什么是ChatGPT中文版？国内可用的ChatGPT中文版镜像网站推荐为什么选ChatGPT中文版ChatGPT官网与中文版的区别如何快速开始使用ChatGPT中文版
  • Python 数据建模完整流程指南 木觞清 3天入门Pythonpython开发语言
    在数据科学和机器学习中，建模是一个至关重要的过程。通过有效的数据建模，我们能够从原始数据中提取有用的洞察，并为预测或分类任务提供支持。在本篇博客中，我们将通过Python展示数据建模的完整流程，包括数据准备、建模、评估和优化等步骤。1.导入必要的库在进行任何数据分析或建模之前，首先需要导入必需的Python库。这些库提供了各种工具和算法，帮助我们更高效地完成任务。importnumpyasnpim
  • 整理一下一些Qt/C++第三方库 MayZork qt开发语言c++
    boost一个广泛的C++库集合，提供了大量的功能模块，包括但不限于数据结构、算法、并发编程、网络编程、文件系统、正则表达式、序列化等。poco也是一个广泛的C++库集合，提供了一套丰富的功能模块，包含网络通信、HTTP、文件系统、XML、JSON、数据库等。libevent轻量级的C语言库，主要用于异步网络编程。它提供了对I/O复用的支持，使得开发者可以在单线程中同时处理多个连接。QCustom
  • C++ 游戏开发 周盛欢 c++开发语言
    嘿，小伙伴们，想不想自己动手开发个游戏呀？今天就来带大家用C++开发游戏，保证通俗易懂，就算你是0基础也能跟上。一、为啥用C++开发游戏C++可厉害了，它运行速度快得跟闪电似的，能让你的游戏画面流畅得跟丝滑巧克力一样。而且它功能强大，啥复杂的游戏逻辑都能搞定，像那些大型的3D游戏，很多都是用C++开发的呢。二、开发环境搭建先得有个好用的开发工具，推荐用VisualStudio（VS）。去官网（ht
  • 随机森林分类算法原理与实验分析 ningaiiii 机器学习与深度学习随机森林分类算法
    随机森林分类算法原理与实验分析1.引言随机森林（RandomForest）是一种集成学习方法，它通过构建多个决策树并结合它们的预测结果来进行分类。你可以把它想象成一个“团队决策”的过程：团队中的每个成员（决策树）都独立发表意见，最后通过投票决定最终结果。这种方法不仅提高了模型的准确性，还增强了模型的稳定性和鲁棒性。随机森林的主要特点是通过随机选择样本和特征来构建多个决策树，从而避免单棵决策树可能产
  • 快速傅里叶变换 华东算法王（原聪明的小孩子 小孩哥总结MIT线性代数线性代数矩阵
    快速傅里叶变换（FFT）快速傅里叶变换（FFT）是一种高效的算法，用于计算离散傅里叶变换（DFT）和其逆变换。傅里叶变换是一种重要的数学工具，广泛应用于信号处理、图像分析、数据压缩、声音合成等领域。传统的离散傅里叶变换算法的计算复杂度较高，而快速傅里叶变换通过减少计算量，大大提高了运算速度。1.离散傅里叶变换（DFT）离散傅里叶变换（DFT）将离散的时间信号变换到频域。对于一个长度为(N)的离散序
  • 动态规划算法----回文串问题 阿_北 算法动态规划c++
    引言在算法的世界里，回文串问题一直是一个经典且富有挑战性的题目。而动态规划作为一种强大的算法思想，为解决这类问题提供了高效且优雅的解决方案。本文将深入探讨如何运用动态规划算法来解决回文串相关问题，从问题描述、动态规划思路，到代码实现与复杂度分析，全面剖析这一过程。回文串问题描述回文串是指一个字符串从左到右读和从右到左读是完全一样的，例如“level”、“madam”等。常见的回文串问题有：给定一个
  • BERT详解 comli_cn 大模型笔记bert人工智能深度学习
    1.背景结构1.1基础知识BERT（BidirectionalEncoderRepresentationsfromTransformers）是谷歌提出，作为一个Word2Vec的替代者，其在NLP领域的11个方向大幅刷新了精度，可以说是前几年来自残差网络最优突破性的一项技术了。论文的主要特点以下几点：使用了双向Transformer作为算法的主要框架，之前的模型是从左向右输入一个文本序列，或者将l
  • 华为OD机试E卷 - 跳格子3 （Java & Python& JS & C++ & C ） 算法大师 最新华为OD机试华为odjavapythonc语言javascriptc++华为OD机试E卷-跳格子3
    最新华为OD机试真题目录：点击查看目录华为OD面试真题精选：点击立即查看题目描述小明和朋友们一起玩跳格子游戏，每个格子上有特定的分数score=[1,-1,-6,7,-17,7]，从起点score[0]开始，每次最大的步长为k，请你返回小明跳到终点score[n-1]时，能得到的最大得分。输入描述第一行输入总的格子数量n第二行输入每个格子的分数score[i]第三行输入最大跳的步长k备注格子的总长
  • 华为OD机试E卷 - 查找接口成功率最优时间段（Java & Python& JS & C++ & C ） 算法大师 最新华为OD机试华为odjavapython华为OD机试E卷javascriptc++
    最新华为OD机试真题目录：点击查看目录华为OD面试真题精选：点击立即查看题目描述服务之间交换的接口成功率作为服务调用关键质量特性，某个时间段内的接口失败率使用一个数组表示，数组中每个元素都是单位时间内失败率数值，数组中的数值为0~100的整数，给定一个数值(minAverageLost)表示某个时间段内平均失败率容忍值，即平均失败率小于等于minAverageLost，找出数组中最长时间段，如果未
  • 华为OD机试CD卷- 跳格子3（Java & Python& JS & C++ & C ） 算法大师 最新华为OD机试华为odc语言c++javajavascript
    题目描述小明和朋友们一起玩跳格子游戏，每个格子上有特定的分数score=[1,-1,-6,7,-17,7]，从起点score[0]开始，每次最大的步长为k，请你返回小明跳到终点score[n-1]时，能得到的最大得分。输入描述第一行输入总的格子数量n第二行输入每个格子的分数score[i]第三行输入最大跳的步长k输出描述输出最大得分备注格子的总长度n和步长k的区间在[1,100000]每个格子的分
  • 第五讲：运算符与表达式：算术、关系、逻辑、赋值等运算符及其优先级 VNGRY C++50讲算法c++
    在C++编程中，运算符和表达式是构建程序逻辑的基础。它们允许我们对数据进行各种操作，从而得出新的数据值或执行特定的逻辑判断。C++中的运算符种类繁多，根据功能的不同，可以大致分为算术运算符、关系运算符、逻辑运算符和赋值运算符等几大类。此外，每种运算符都有其特定的优先级和结合性，这些规则决定了在复杂的表达式中，各个运算符的执行顺序。一、算术运算符算术运算符用于执行基本的数学运算，包括加法、减法、乘法
  • JVM StackMapTable 属性的作用及理解 lijingyao8206 jvm字节码Class文件StackMapTable
            在Java 6版本之后JVM引入了栈图(Stack Map Table)概念。为了提高验证过程的效率，在字节码规范中添加了Stack Map Table属性，以下简称栈图，其方法的code属性中存储了局部变量和操作数的类型验证以及字节码的偏移量。也就是一个method需要且仅对应一个Stack Map Table。在Java 7版
  • 回调函数调用方法 百合不是茶 java
    最近在看大神写的代码时,.发现其中使用了很多的回调 ,以前只是在学习的时候经常用到 ,现在写个笔记 记录一下   代码很简单:           MainDemo  :调用方法  得到方法的返回结果        
  • [时间机器]制造时间机器需要一些材料 comsci 制造
          根据我的计算和推测,要完全实现制造一台时间机器,需要某些我们这个世界不存在的物质     和材料...       甚至可以这样说,这种材料和物质,我们在反应堆中也无法获得......      
  • 开口埋怨不如闭口做事 邓集海 邓集海 做人 做事 工作
    “开口埋怨，不如闭口做事。”不是名人名言，而是一个普通父亲对儿子的训导。但是，因为这句训导，这位普通父亲却造就了一个名人儿子。这位普通父亲造就的名人儿子，叫张明正。 　　 　　张明正出身贫寒，读书时成绩差，常挨老师批评。高中毕业，张明正连普通大学的分数线都没上。高考成绩出来后，平时开口怨这怨那的张明正，不从自身找原因，而是不停地埋怨自己家庭条件不好、埋怨父母没有给他创造良好的学习环境。 　　 　　
  • jQuery插件开发全解析，类级别与对象级别开发 IT独行者 jquery开发插件　函数
    jQuery插件的开发包括两种： 一种是类级别的插件开发，即给 jQuery添加新的全局函数，相当于给 jQuery类本身添加方法。 jQuery的全局函数就是属于 jQuery命名空间的函数，另一种是对象级别的插件开发，即给 jQuery对象添加方法。下面就两种函数的开发做详细的说明。   1 、类级别的插件开发 类级别的插件开发最直接的理解就是给jQuer
  • Rome解析Rss 413277409 Rome解析Rss
    import java.net.URL;  import java.util.List;    import org.junit.Test;    import com.sun.syndication.feed.synd.SyndCategory;  import com.sun.syndication.feed.synd.S
  • RSA加密解密 无量 加密解密rsa
    RSA加密解密代码 代码有待整理 package com.tongbanjie.commons.util; import java.security.Key; import java.security.KeyFactory; import java.security.KeyPair; import java.security.KeyPairGenerat
  • linux 软件安装遇到的问题 aichenglong linux遇到的问题ftp
    1 ftp配置中遇到的问题    500 OOPS: cannot change directory   出现该问题的原因:是SELinux安装机制的问题.只要disable SELinux就可以了   修改方法:1 修改/etc/selinux/config 中SELINUX=disabled    2 source /etc
  • 面试心得 alafqq 面试
    最近面试了好几家公司。记录下； 支付宝，面试我的人胖胖的，看着人挺好的；博彦外包的职位，面试失败； 阿里金融，面试官人也挺和善，只不过我让他吐血了。。。 由于印象比较深，记录下； 1，自我介绍 2，说下八种基本类型；（算上string。楼主才答了3种，哈哈，string其实不是基本类型，是引用类型） 3，什么是包装类，包装类的优点； 4，平时看过什么书？NND，什么书都没看过。。照样
  • java的多态性探讨 百合不是茶 java
    java的多态性是指main方法在调用属性的时候类可以对这一属性做出反应的情况 //package 1; class A{ public void test(){ System.out.println("A"); } } class D extends A{ public void test(){ S
  • 网络编程基础篇之JavaScript-学习笔记 bijian1013 JavaScript
    1.documentWrite <html> <head> <script language="JavaScript"> document.write("这是电脑网络学校"); document.close(); </script> </h
  • 探索JUnit4扩展：深入Rule bijian1013 JUnitRule单元测试
            本文将进一步探究Rule的应用，展示如何使用Rule来替代@BeforeClass，@AfterClass，@Before和@After的功能。         在上一篇中提到，可以使用Rule替代现有的大部分Runner扩展，而且也不提倡对Runner中的withBefores()，withAfte
  • [CSS]CSS浮动十五条规则 bit1129 css
    这些浮动规则，主要是参考CSS权威指南关于浮动规则的总结，然后添加一些简单的例子以验证和理解这些规则。   1. 所有的页面元素都可以浮动 2. 一个元素浮动后，会成为块级元素，比如<span>,a, strong等都会变成块级元素 3.一个元素左浮动，会向最近的块级父元素的左上角移动，直到浮动元素的左外边界碰到块级父元素的左内边界；如果这个块级父元素已经有浮动元素停靠了
  • 【Kafka六】Kafka Producer和Consumer多Broker、多Partition场景 bit1129 partition
    0.Kafka服务器配置 3个broker 1个topic，6个partition，副本因子是2 2个consumer，每个consumer三个线程并发读取   1. Producer package kafka.examples.multibrokers.producers; import java.util.Properties; import java.util.
  • zabbix_agentd.conf配置文件详解 ronin47 zabbix 配置文件
    Aliaskey的别名，例如 Alias=ttlsa.userid:vfs.file.regexp[/etc/passwd,^ttlsa:.:([0-9]+),,,,\1]， 或者ttlsa的用户ID。你可以使用key：vfs.file.regexp[/etc/passwd,^ttlsa:.: ([0-9]+),,,,\1]，也可以使用ttlsa.userid。备注: 别名不能重复，但是可以有多个
  • java--19.用矩阵求Fibonacci数列的第N项 bylijinnan fibonacci
    参考了网上的思路，写了个Java版的： public class Fibonacci { final static int[] A={1,1,1,0}; public static void main(String[] args) { int n=7; for(int i=0;i<=n;i++){ int f=fibonac
  • Netty源码学习-LengthFieldBasedFrameDecoder bylijinnan javanetty
    先看看LengthFieldBasedFrameDecoder的官方API http://docs.jboss.org/netty/3.1/api/org/jboss/netty/handler/codec/frame/LengthFieldBasedFrameDecoder.html API举例说明了LengthFieldBasedFrameDecoder的解析机制，如下： 实
  • AES加密解密 chicony 加密解密
    AES加解密算法，使用Base64做转码以及辅助加密： package com.wintv.common; import javax.crypto.Cipher; import javax.crypto.spec.IvParameterSpec; import javax.crypto.spec.SecretKeySpec; import sun.misc.BASE64Decod
  • 文件编码格式转换 ctrain 编码格式
    package com.test; import java.io.File; import java.io.FileInputStream; import java.io.FileOutputStream; import java.io.IOException; import java.io.InputStream; import java.io.OutputStream;
  • mysql 在linux客户端插入数据中文乱码 daizj mysql中文乱码
    1、查看系统客户端，数据库，连接层的编码  查看方法： http://daizj.iteye.com/blog/2174993 进入mysql，通过如下命令查看数据库编码方式： mysql>  show variables like 'character_set_%'; +--------------------------+------
  • 好代码是廉价的代码 dcj3sjt126com 程序员读书
      长久以来我一直主张：好代码是廉价的代码。 当我跟做开发的同事说出这话时，他们的第一反应是一种惊愕，然后是将近一个星期的嘲笑，把它当作一个笑话来讲。 当他们走近看我的表情、知道我是认真的时，才收敛一点。 当最初的惊愕消退后，他们会用一些这样的话来反驳： “好代码不廉价，好代码是采用经过数十年计算机科学研究和积累得出的最佳实践设计模式和方法论建立起来的精心制作的程序代码。” 我只
  • Android网络请求库——android-async-http dcj3sjt126com android
    在iOS开发中有大名鼎鼎的ASIHttpRequest库，用来处理网络请求操作，今天要介绍的是一个在Android上同样强大的网络请求库android-async-http，目前非常火的应用Instagram和Pinterest的Android版就是用的这个网络请求库。这个网络请求库是基于Apache HttpClient库之上的一个异步网络请求处理库，网络处理均基于Android的非UI线程，通
  • ORACLE 复习笔记之SQL语句的优化 eksliang SQL优化Oracle sql语句优化SQL语句的优化
    转载请出自出处：http://eksliang.iteye.com/blog/2097999   SQL语句的优化总结如下   sql语句的优化可以按照如下六个步骤进行： 合理使用索引 避免或者简化排序 消除对大表的扫描 避免复杂的通配符匹配 调整子查询的性能 EXISTS和IN运算符 下面我就按照上面这六个步骤分别进行总结：
  • 浅析：Android 嵌套滑动机制（NestedScrolling） gg163 android移动开发滑动机制嵌套
    谷歌在发布安卓 Lollipop版本之后，为了更好的用户体验，Google为Android的滑动机制提供了NestedScrolling特性 NestedScrolling的特性可以体现在哪里呢？<!--[if !supportLineBreakNewLine]--><!--[endif]--> 比如你使用了Toolbar，下面一个ScrollView，向上滚
  • 使用hovertree菜单作为后台导航 hvt JavaScriptjquery.nethovertreeasp.net
      hovertree是一个jquery菜单插件，官方网址：http://keleyi.com/jq/hovertree/ ，可以登录该网址体验效果。 0.1.3版本：http://keleyi.com/jq/hovertree/demo/demo.0.1.3.htm hovertree插件包含文件： http://keleyi.com/jq/hovertree/css
  • SVG 教程 （二）矩形 天梯梦 svg
    SVG <rect> SVG Shapes SVG有一些预定义的形状元素，可被开发者使用和操作： 矩形 <rect> 圆形 <circle> 椭圆 <ellipse> 线 <line> 折线 <polyline> 多边形 <polygon> 路径 <path>
  • 一个简单的队列 luyulong java数据结构队列
    public class MyQueue { private long[] arr; private int front; private int end; // 有效数据的大小 private int elements; public MyQueue() { arr = new long[10]; elements = 0; front
  • 基础数据结构和算法九：Binary Search Tree sunwinner Algorithm
      A binary search tree (BST) is a binary tree where each node has a Comparable key (and an associated value) and satisfies the restriction that the key in any node is larger than the keys in all
  • 项目出现的一些问题和体会 Steven-Walker DAOWebservlet
         第一篇博客不知道要写点什么，就先来点近阶段的感悟吧。     这几天学了servlet和数据库等知识，就参照老方的视频写了一个简单的增删改查的，完成了最简单的一些功能，使用了三层架构。 dao层完成的是对数据库具体的功能实现，service层调用了dao层的实现方法，具体对servlet提供支持。  &
  • 高手问答：Java老A带你全面提升Java单兵作战能力！ ITeye管理员 java
    本期特邀《Java特种兵》作者：谢宇，CSDN论坛ID: xieyuooo 针对JAVA问题给予大家解答，欢迎网友积极提问，与专家一起讨论! 作者简介： 淘宝网资深Java工程师，CSDN超人气博主，人称“胖哥”。 CSDN博客地址： http://blog.csdn.net/xieyuooo 作者在进入大学前是一个不折不扣的计算机白痴，曾经被人笑话过不懂鼠标是什么，
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他