LFM算法——推荐系统
在日常生活中，人们实际上经常使用这种方法，如你哪天突然想看个电影，但你不知道具体看哪部，你会怎么做？大部分的人会问问周围的朋友，最近有什么好看的电影，而我们一般更倾向于从兴趣或观点相近的朋友那里得到推荐。这就是协同过滤的思想
LFM（latent factor model 隐语义模型）算法背景
https://www.cnblogs.com/ventlam/p/6296255.html，这里有详细介绍
https://blog.csdn.net/codes_first/article/details/80796151
https://zhuanlan.zhihu.com/p/28023308 L1&L2个正则化项
也是矩阵分解的一种，隐语义模型
什么是LFM算法
spark ALS是其中一种实现
- 1、根据用户对item点击与否等，来获取用户item之间关系，item和item之间的关系等
- 2、输入：user对item点展矩阵，模型参数：每一个user的向量表示和每个item的向量表示，行向量乘以列向量是一个常数，user向量和item向量相乘，完全可以拟合点展矩阵中的数值
LFM算法应用场景
1、完成user的item推荐列表
获取到用户toplike
2、完成item的相似度列表
获取到item的topsim（item向量得到，可以计算每个item的相似度矩阵）
3、完成item之间隐含topic的挖掘
计算item的topic，使用聚类方法，将item聚合成为不同的类，根据类别推荐
LFM算法例子
对于音乐，每一个用户都有自己的喜好，比如A喜欢带有小清新的、吉他伴奏的、王菲等元素（latent factor），如果一首歌（item）带有这些元素，那么就将这首歌推荐给该用户，也就是用元素去连接用户和音乐。每个人对不同的元素偏好不同，而每首歌包含的元素也不一样。
所以，我们希望能找到这样两个矩阵：潜在因子-用户矩阵Q、潜在因子-音乐矩阵P
（1）潜在因子-用户矩阵：表示不同的用户对于不用元素的偏好程度，1代表很喜欢，0代表不喜欢。
比如：
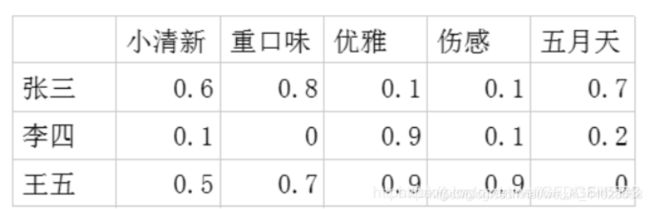（2）潜在因子-音乐矩阵：表示每种音乐含有各种元素的成分，比如下表中，音乐A是一个偏小清新的音乐，含有小清新这个Latent Factor的成分是0.9，重口味的成分是0.1，优雅的成分是0.2……
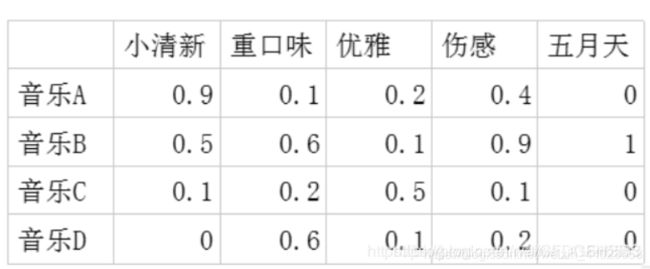利用这两个矩阵，我们能得出张三对音乐A的喜欢程度是：张三对小清新的偏好音乐A含有小清新的成分+对重口味的偏好音乐A含有重口味的成分+对优雅的偏好音乐A含有优雅的成分+……
即：0.6x0.9 + 0.8x0.1 + 0.1x0.2 + 0.1x0.4 + 0.7x0 = 0.68
每个用户对每首歌都这样计算可以得到不同用户对不同歌曲的评分矩阵。（注，这里的破浪线表示的是估计的评分，接下来我们还会用到不带波浪线的R表示实际的评分）：
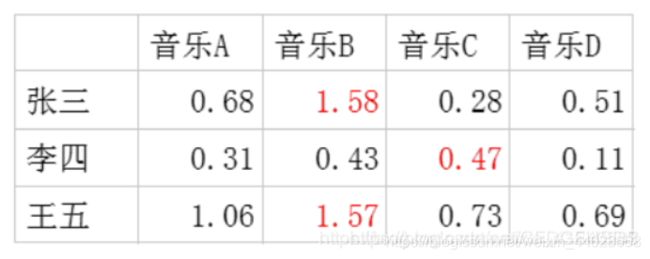因此我们队张三推荐四首歌中得分最高的B，对李四推荐得分最高的C，王五推荐B。
基于上面的思想，基于兴趣分类的方法大概需要解决3个问题：
- ①：如何对物品分类
- ②：如何确定用户对哪些物品分类，以及感兴趣的程度
- ③：确定了用户的兴趣，选择这个类的哪些物品推荐给用户？以及如何确定这些物品在这个类中的权重？
下面问题来了，这个潜在因子（latent factor）是怎么得到的呢？
由于面对海量的让用户自己给音乐分类并告诉我们自己的偏好系数显然是不现实的，事实上我们能获得的数据只有用户行为数据。我们沿用 @邰原朗的量化标准：单曲循环=5, 分享=4, 收藏=3, 主动播放=2 , 听完=1, 跳过=-2 , 拉黑=-5，在分析时能获得的实际评分矩阵R，也就是输入矩阵大概是这个样子：
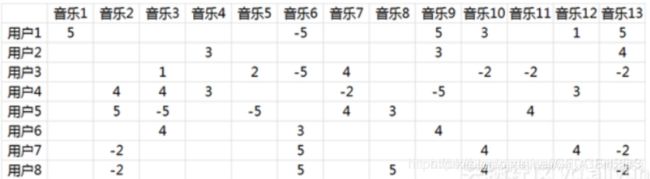事实上这是个非常非常稀疏的矩阵，因为大部分用户只听过全部音乐中很少一部分。如何利用这个矩阵去找潜在因子呢？这里主要应用到的是矩阵的UV分解。也就是将上面的评分矩阵分解为两个低维度的矩阵，用Q和P两个矩阵的乘积去估计实际的评分矩阵，而且我们希望估计的评分矩阵
LFM建模公式
p ( u , i ) = p u T q i = ∑ f = 1 F p u f q i f p(u, i)=p_{u}^{T} q_{i}=\sum_{f=1}^{F} p_{u f} q_{i f} p(u,i)=puTqi=∑f=1Fpufqif
u-user ；i-item；如果user 点击了item p(u,i)= 1,否则为0，F是向量维度（user对item的影响因素的个数），如何获取到pu,qi，使用监督学习（随机数初始化），然后迭代，无限接近
LFM loss function（平方损失函数）
loss = ∑ ( u , i ) ∈ D ( p ( u , i ) − p L F M ( u , i ) ) 2 \operatorname{loss}=\sum_{(u, i) \in D}\left(p(u, i)-p^{L F M}(u, i)\right)^{2} loss=∑(u,i)∈D(p(u,i)−pLFM(u,i))2
D-所有训练样本的集合
第一个参数：user是否点击item，点击为1，否则0
第二个参数：模型预估的user对item的喜好程度
L2正则化，增强泛化能力
loss = ∑ ( n , i ) ∈ D ( p ( u , i ) − ∑ f = 1 F p u f q i f ) + ∂ k ∣ p u ∣ 2 + ∂ ∣ q i ∣ 2 \operatorname{loss}=\sum_{(n, i) \in D}\left(p(u, i)-\sum_{f=1}^{F} p_{u f} q_{i f}\right)+\partial_{k}\left|p_{u}\right|^{2}+\partial\left|q_{i}\right|^{2} loss=∑(n,i)∈D(p(u,i)−∑f=1Fpufqif)+∂k∣pu∣2+∂∣qi∣2
∂ l o s s ∂ p u f = − 2 ( p ( u , i ) − p L F M ( u , i ) ) q i f + 2 ∂ p u f p u f = p u f − β ∂ l o s s ∂ p u f ∂ l o s s ∂ q i j = − 2 ( p ( u , i ) − p L F M ( u , i ) ) p u f + 2 ∂ q i j q i f = q i f − β ∂ l o s s ∂ q i f \begin{array}{ll}\frac{\partial l o s s}{\partial p_{u f}}=-2\left(p(u, i)-p^{L F M}(u, i)\right) q_{i f}+2 \partial p_{u f} & p_{u f}=p_{u f}-\beta \frac{\partial l o s s}{\partial p_{u f}} \\ \frac{\partial l o s s}{\partial q_{i j}}=-2\left(p(u, i)-p^{L F M}(u, i)\right) p_{u f}+2 \partial q_{i j} & q_{i f}=q_{i f}-\beta \frac{\partial l o s s}{\partial q_{i f}}\end{array} ∂puf∂loss=−2(p(u,i)−pLFM(u,i))qif+2∂puf∂qij∂loss=−2(p(u,i)−pLFM(u,i))puf+2∂qijpuf=puf−β∂puf∂lossqif=qif−β∂qif∂loss
求偏导，β是学习率
采样
- 负样本的选取，因为比起正样本，用户的负样本是非常多的,因为展现给用户的item比用户点击的item要多的多，所以需要选取那些充分展现（该item在所有用户中已经有了比较高的item展现次数，我们就可以用用户没有点击的物品中，按照该item在所有用户中的展现次数做降序，去一定数量的item，作为负样本，保证正负样本的均衡）的而用户没有点击的item，作为负样本
- 隐特征F，正则参数α，学习率learn rate 在实验的时候，固定α=0.02，λ=0.01，然后变化F个数，来训练模型，模型快速收敛
- 主要目的是求P（user-class）,Q矩阵(class,item)，通过，代码实现参考 F-隐特征，T-迭代次数，alpha
学习率，lamb正则化参数
梯度概念：https://blog.csdn.net/walilk/article/details/50978864 def
def LatentFactorModel(user_items, F, T, alpha, lamb):
# https: // blog.csdn.net / codes_first / article / details / 80796151
InitAllItemSet(user_items)
# 初始化P，Q矩阵
[P, Q] = InitModel(user_items, F)
# 开始迭代
for step in range(0, T):
# 从数据集中一次取出user以及该user喜欢的items集合
for user, items in user_items.items():
# 随机抽样 为user抽取与items数据量相当的负样本，并且与负样本合并，用户优化技术
samples = RandSelectNegativeSample(items)
# 依次取出item和user对该item的兴趣度
# Python 字典(Dictionary) items() 函数以列表返回可遍历的(键, 值) 元组数组。
for item, rui in samples.items():
# 根据当前参数计算误差，就是矩阵乘法公式
eui = rui - Predict(user, item, P, Q)
# 优化参数
for f in range(0, F):
P[user][f] += alpha * (eui * Q[item][f] - lamb * P[user][f])
Q[item][f] += alpha * (eui * P[user][f] - lamb * Q[item][f])
# 每次迭代完成要降低学习率，一开始由于最优化值相差元，下降快
# 当优化到一定程度，需要放慢学习率，慢慢接近最优值
alpha *= 0.9
return P, Q
def Predict(user, item, P, Q):
rate = 0
for f, puf in P[user].items():
qif = Q[item][f]
rate += puf * qif
return rate
参考自：一种tang两种味