五分钟学算法：Top K 问题的两种经典解法

点击关注上方“五分钟学算法”，

设为“置顶或星标”，第一时间送达干货。

转自面向大象编程，作者nettee

题目描述

这是一道经典的面试题了，也叫做 “Top K 问题”。解决这个问题有两种常用的方法：堆方法、分治法。分治法的思想和快速排序相同。

本篇题解分别讲解了两种方法，并比较了它们的适用场景。

题目解析

这道题是一个经典的 Top K 问题，是面试中的常客。Top K 问题有两种不同的解法，一种解法使用堆（优先队列），另一种解法使用类似快速排序的分治法。这两种方法各有优劣，最好都掌握。本文用图解的形式讲解这道问题的两种解法，包括三个部分：

• 方法一：堆，时间复杂度

• 方法二：快排变形，（平均）时间复杂度

• 两种方法的优劣比较

方法一：堆

比较直观的想法是使用堆数据结构来辅助得到最小的 k 个数。堆的性质是每次可以找出最大或最小的元素。我们可以使用一个大小为 k 的最大堆（大顶堆），将数组中的元素依次入堆，当堆的大小超过 k 时，便将多出的元素从堆顶弹出。我们以数组 ， 为例展示元素入堆的过程，如下面动图所示：

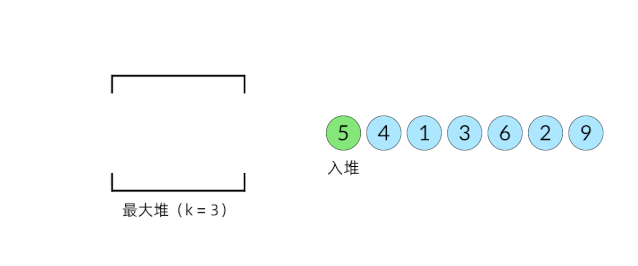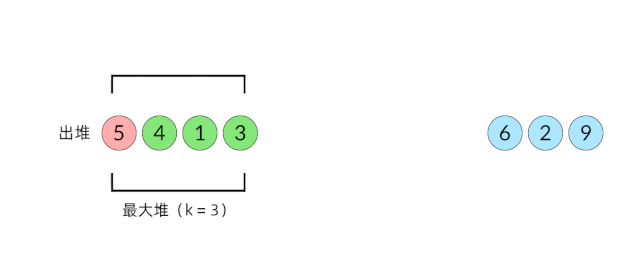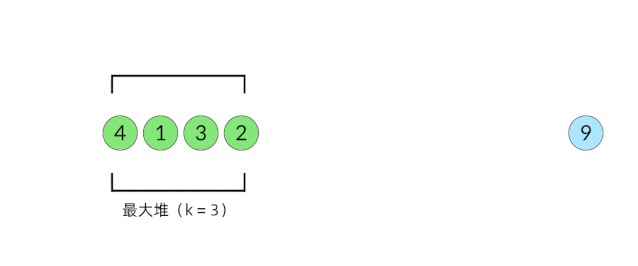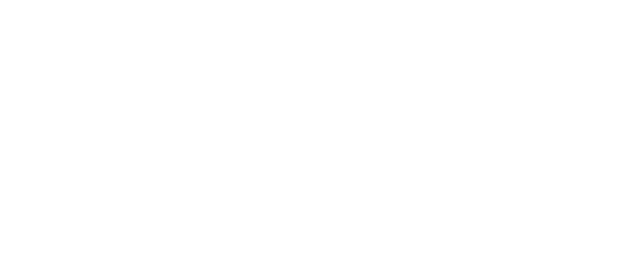入堆出堆的过程

这样，由于每次从堆顶弹出的数都是堆中最大的，最小的 k 个元素一定会留在堆里。这样，把数组中的元素全部入堆之后，堆中剩下的 k 个元素就是最大的 k 个数了。

注意在动画中，我们并没有画出堆的内部结构，因为这部分内容并不重要。我们只需要知道堆每次会弹出最大的元素即可。在写代码的时候，我们使用的也是库函数中的优先队列数据结构，如 Java 中的 PriorityQueue。在面试中，我们不需要实现堆的内部结构，把数据结构使用好，会分析其复杂度即可。

以下是题解代码。感谢评论区提醒，这里的代码可以做一些优化，如果当前数字不小于堆顶元素，数字可以直接丢掉，不入堆。下方的代码已更新：

public int[] getLeastNumbers(int[] arr, int k) {
    if (k == 0) {
        return new int[0];
    }
    // 使用一个最大堆（大顶堆）
    // Java 的 PriorityQueue 默认是小顶堆，添加 comparator 参数使其变成最大堆
    Queue heap = new PriorityQueue<>(k, (i1, i2) -> Integer.compare(i2, i1));

    for (int e : arr) {
        // 当前数字小于堆顶元素才会入堆
        if (heap.isEmpty() || heap.size() < k || e < heap.peek()) {
            heap.offer(e);
        }
        if (heap.size() > k) {
            heap.poll(); // 删除堆顶最大元素
        }
    }

    // 将堆中的元素存入数组
    int[] res = new int[heap.size()];
    int j = 0;
    for (int e : heap) {
        res[j++] = e;
    }
    return res;
}

算法的复杂度分析：

• 由于使用了一个大小为 k 的堆，空间复杂度为 ；

• 入堆和出堆操作的时间复杂度均为 ，每个元素都需要进行一次入堆操作，故算法的时间复杂度为 。

方法二：快排变形

Top K 问题的另一个解法就比较难想到，需要在平时有算法的积累。实际上，“查找第 k 大的元素”是一类算法问题，称为选择问题。找第 k 大的数，或者找前 k 大的数，有一个经典的 quick select（快速选择）算法。这个名字和 quick sort（快速排序）看起来很像，算法的思想也和快速排序类似，都是分治法的思想。

让我们回顾快速排序的思路。快速排序中有一步很重要的操作是 partition（划分），从数组中随机选取一个枢纽元素 v，然后原地移动数组中的元素，使得比 v 小的元素在 v 的左边，比 v 大的元素在 v 的右边，如下图所示：

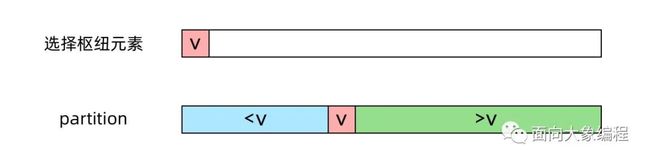partition 示意图

这个 partition 操作是原地进行的，需要 的时间，接下来，快速排序会递归地排序左右两侧的数组。而快速选择（quick select）算法的不同之处在于，接下来只需要递归地选择一侧的数组。快速选择算法想当于一个“不完全”的快速排序，因为我们只需要知道最小的 k 个数是哪些，并不需要知道它们的顺序。

我们的目的是寻找最小的 个数。假设经过一次 partition 操作，枢纽元素位于下标 ，也就是说，左侧的数组有 个元素，是原数组中最小的 个数。那么：

• 若 ，我们就找到了最小的 个数，就是左侧的数组；

• 若 ，则最小的 个数一定都在左侧数组中，我们只需要对左侧数组递归地 partition 即可；

• 若 ，则左侧数组中的 个数都属于最小的 个数，我们还需要在右侧数组中寻找最小的 个数，对右侧数组递归地 partition 即可。

这种方法需要多加领会思想，如果你对快速排序掌握得很好，那么稍加推导应该不难掌握 quick select 的要领。

以下是题解代码：

public int[] getLeastNumbers(int[] arr, int k) {
    if (k == 0) {
        return new int[0];
    } else if (arr.length <= k) {
        return arr;
    }
    
    // 原地不断划分数组
    partitionArray(arr, 0, arr.length - 1, k);
    
    // 数组的前 k 个数此时就是最小的 k 个数，将其存入结果
    int[] res = new int[k];
    for (int i = 0; i < k; i++) {
        res[i] = arr[i];
    }
    return res;
}

void partitionArray(int[] arr, int lo, int hi, int k) {
    // 做一次 partition 操作
    int m = partition(arr, lo, hi);
    // 此时数组前 m 个数，就是最小的 m 个数
    if (k == m) {
        // 正好找到最小的 k(m) 个数
        return;
    } else if (k < m) {
        // 最小的 k 个数一定在前 m 个数中，递归划分
        partitionArray(arr, lo, m-1, k);
    } else {
        // 在右侧数组中寻找最小的 k-m 个数
        partitionArray(arr, m+1, hi, k);
    }
}

// partition 函数和快速排序中相同，具体可参考快速排序相关的资料
// 代码参考 Sedgewick 的《算法4》
int partition(int[] a, int lo, int hi) {
    int i = lo;
    int j = hi + 1;
    int v = a[lo];
    while (true) {
        while (a[++i] < v) {
            if (i == hi) {
                break;
            }
        }
        while (a[--j] > v) {
            if (j == lo) {
                break;
            }
        }

        if (i >= j) {
            break;
        }
        swap(a, i, j);
    }
    swap(a, lo, j);

    // a[lo .. j-1] <= a[j] <= a[j+1 .. hi]
    return j;
}

void swap(int[] a, int i, int j) {
    int temp = a[i];
    a[i] = a[j];
    a[j] = temp;
}

上述代码中需要注意一个细节（评论区有好几个小伙伴问到，这里补充说明一下）：

partitionArray 函数中，两次递归调用传入的参数为什么都是 k？特别是第二个调用，我们在右侧数组中寻找最小的 k-m 个数，但是对于整个数组而言，这是最小的 k 个数。所以说，函数调用传入的参数应该为 k。

该代码的成绩还是非常好的：

算法的复杂度分析：

• 空间复杂度 ，不需要额外空间。

• 时间复杂度的分析方法和快速排序类似。由于快速选择只需要递归一边的数组，时间复杂度小于快速排序，期望时间复杂度为 ，最坏情况下的时间复杂度为 。

两种方法的优劣性比较

在面试中，另一个常常问的问题就是这两种方法有何优劣。看起来分治法的快速选择算法的时间、空间复杂度都优于使用堆的方法，但是要注意到快速选择算法的几点局限性：

第一，算法需要修改原数组，如果原数组不能修改的话，还需要拷贝一份数组，空间复杂度就上去了。

第二，算法需要保存所有的数据。如果把数据看成输入流的话，使用堆的方法是来一个处理一个，不需要保存数据，只需要保存 k 个元素的最大堆。而快速选择的方法需要先保存下来所有的数据，再运行算法。当数据量非常大的时候，甚至内存都放不下的时候，就麻烦了。

所以当数据量大的时候还是用基于堆的方法比较好。

END

---

● 二叉树问题太复杂？「三步走」方法解决它！

● 五分钟学算法：什么是堆？

● 一个我超喜欢的动态博客系统，五分钟即可部署上线！

● 五分钟学算法：什么是线段树？

点“在看”你懂得