CUDA PYTHON 矩阵相乘

一、CUDA线程索引

线程索引即如何根据线程层次中的blockId，gridId以及threadId确定线程的确切下标。可以把线程确切的下标理解为一个唯一的线程索引表示，它和线程层次中的每一个线程都是一一对应的。线程层次参看前一篇文章 CUDA PYTHON并行计算基础。例如下方图示所给出的计算方法。
对于一维的情况，如果一个Block有8个Thread，则第3个Block（下标为2，因为从0开始）的第5个Thread的确切下标就是8 x 2
+5 = 21：

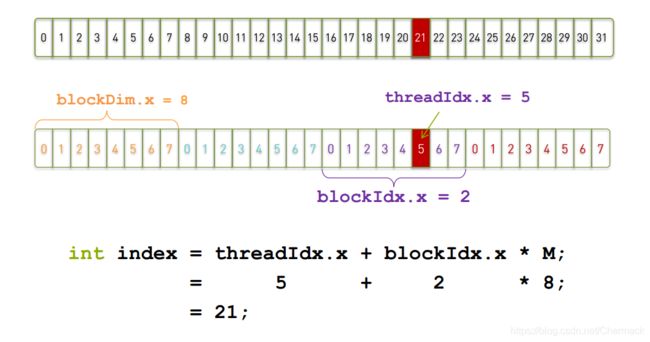
如果是针对二维的情况，计算将要复杂一些，索引分为x方向和y方向两个下标。下图中的一个Grid在x方向维度大小为3，在y方向维度大小为2；一个Block在x方向维度大小为4，在y方向维度大小为3。Thread_x与Thread_y分别表示为线程在x方向和y方向的索引。

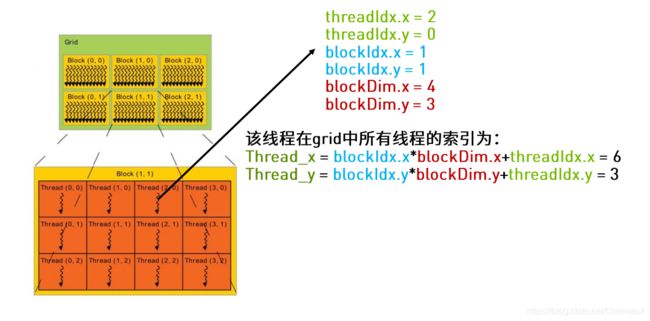
如果将上方的层次模型进行展开如下图所示，将会对计算公式有一个更清晰的认识。


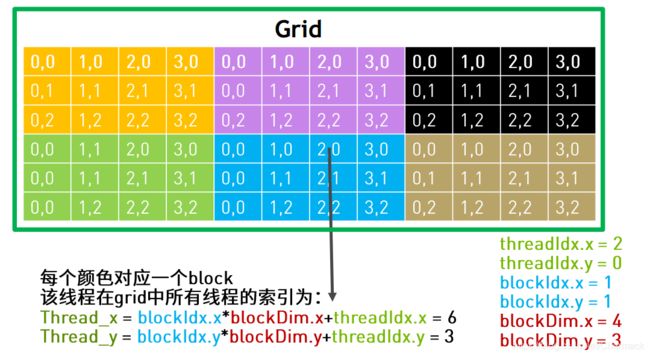
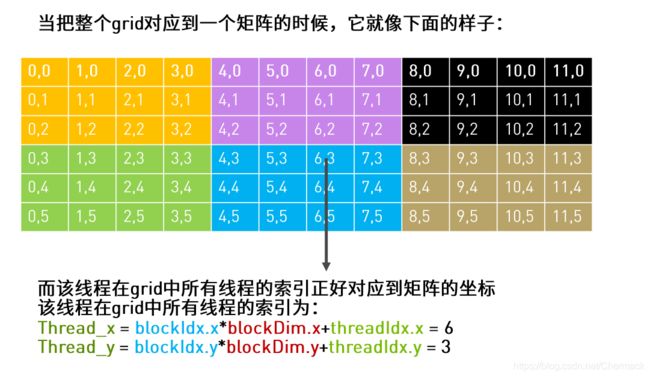
如果需要处理的任务数量超过了设备所拥有和定义的线程数量（一般来说对于一个GPU设备只有一个Grid），可以采用Grid跨步（grid-stride loop） 的方法处理，即将需要处理的任务划分为多个子任务，使单个子任务能够被一个grid处理。Grid会遍历整个任务的划分依次进行执行，直到计算完所有的任务。

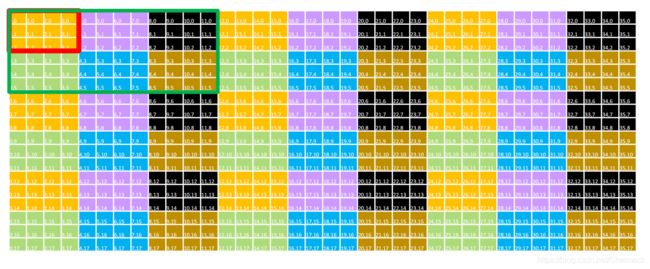
如上图，绿色的框线内为一个Grid，红色框线内为一个Block，一个单元格为一个线程任务。图中单元格的颜色相同表示这些任务将会被同一个Block中的线程执行，通过上图不难看出每个Block内的每个线程将会执行9个任务。
具体的代码实现如下，stride_x和stide_y定义了跨步的步长，通过下方代码可以将任务划分到不同的线程中去执行。

二、CUDA矩阵计算

1、卷积计算

我们知道卷积计算的底层本质上还是矩阵计算，通过定义卷积核，并在图片上滑动的进行矩阵运算，可以进行图片特征的提取。一个动图展示其计算过程

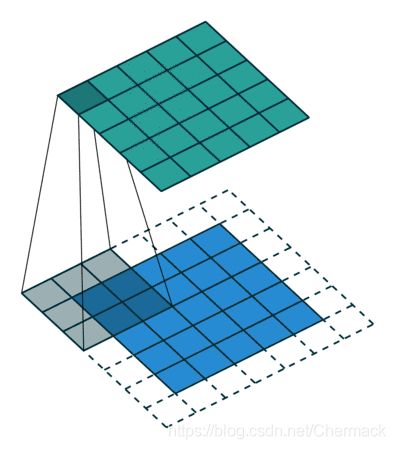
在一张图片的RGB模型表示中，颜色分为红绿蓝三通道，卷积操作时针对三通道应用不同的卷积核进行特征提取操作。因为GPU设备处理单元多，可以将这些通道和卷积核进行合理的拼接，将多个通道的卷积计算合并成大的两个矩阵相乘，这一思想即使用空间换取时间，使得更多的GPU计算单元能够同时进行卷积计算任务的处理。

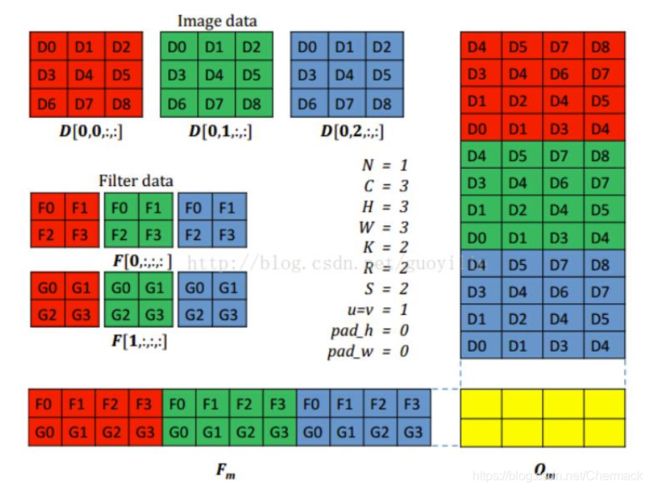
2、矩阵相乘

知道了卷积计算的本质以及如何进行计算过程的转化，那么下面重点讨论如何使用GPU进行矩阵相乘任务。
线性代数中都讲到，两个矩阵M,N相乘的结果P，为M的对应行与N的对应列中的元素对应相乘再相加，得到P中对应某以元素的结果。

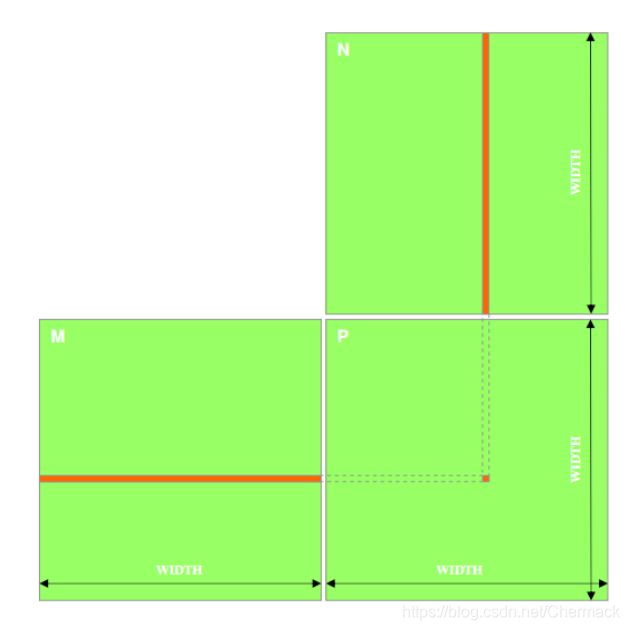
在CPU上进行矩阵的乘法运算，通常需要遍历最终结果P的行数乘列数次，并且每一次中又嵌套了某一行一列的相乘相加操作。
故一般来说矩阵的乘法时间复杂度为O（n³），是一项耗时的操作。

我们知道，矩阵相乘的每一个一行乘以一列的操作，都是相互独立互不干扰的，因此矩阵乘法计算其实可以拆分为若干行乘列的子任务相加求和，最后拼接成一个完成的结果。这一计算要求正和CUDA编程层次类似，因此可以将行列遍历的任务按照线程层次根据不同的grid和Block划分到不同的线程中，省去了CPU计算中的最外层两个循环，应用空间换时间的思想，加大了任务处理的并行度。
利用cuda进行矩阵乘法的计算，只有累计相乘相加中用到了一层循环。

上述代码中，一个Block负责计算该矩阵相乘的一个子集结果，一个线程中执行的任务即是从做左矩阵M中取一行与右矩阵N中取一列做相乘相加并设置结果集中对应元素的结果。所有的Block完成计算，其所有子集的结果拼接就是矩阵相乘的最后结果。

三、CUDA共享内存

矩阵相乘从CPU到GPU已经很大的提升了并行度，在数据规模较大时二者将产生很大的性能差距。但是GPU进行矩阵计算仍然拥有改进空间，即从内存入手。从上一篇《CUDA PYTHON 并行计算基础》中已经提到过GPU设备的内存又分为global memory（全局内存）和（shared memory）共享内存。如果没有做内存优化，数据默认都是存储在global memory中的。而我们在做矩阵相乘时，每一次都要去global memory中读取数据，会增大时间开销，如果能够让计算数据加载到shared memory，离GPU的运算单元更近一些，就能提升程序运行的性能。

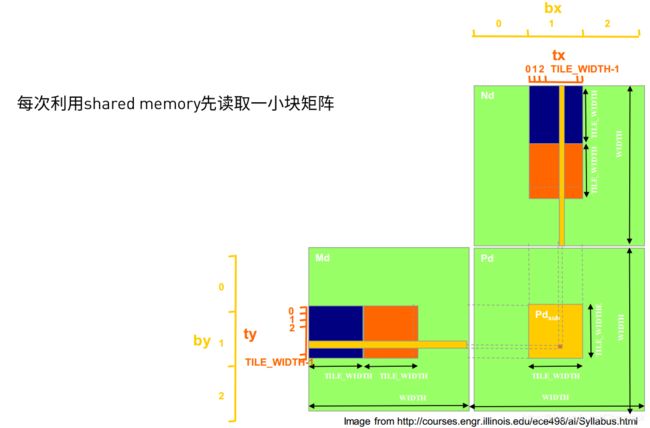
通过将原来M与N矩阵中的某一块需要计算的数据提前缓存到共享内存中，计算时便不会每一次都到全局内存中去加载数据，提高计算效率。

四、CUDA python 矩阵相乘代码实践

环境要求：

• python3.6+
• numba
• cudatoolkit

代码：

#!/usr/bin/env python
# -*- coding:utf-8 -*-
from numba import cuda, float32
import numba
import numpy
import math
import time

TPB = 16

@numba.jit(nopython=True)
def matmul_cpu(A, B, C):
    for y in range(B.shape[1]):
        for x in range(A.shape[0]):
            tmp = 0.
            for k in range(A.shape[1]):
                tmp += A[x, k] * B[k, y]
            C[x, y] = tmp


@cuda.jit()
def matmul_gpu(A, B, C):
    row, col = cuda.grid(2)
    if row < C.shape[0] and col < C.shape[1]:
        tmp = 0.
        for k in range(A.shape[1]):
            tmp += A[row, k] * B[k, col]
        C[row, col] = tmp


@cuda.jit()
def matmul_shared_mem(A, B, C):
    sA = cuda.shared.array((TPB, TPB), dtype=float32)
    sB = cuda.shared.array((TPB, TPB), dtype=float32)
    x, y = cuda.grid(2)

    tx = cuda.threadIdx.x
    ty = cuda.threadIdx.y
    if x >= C.shape[0] and y >= C.shape[1]:
        return
    tmp = 0.
    for i in range(int(A.shape[1] / TPB)):
        sA[tx, ty] = A[x, ty + i * TPB]
        sB[tx, ty] = B[tx + i * TPB, y]
        cuda.syncthreads()
        for j in range(TPB):
            tmp += sA[tx, j] * sB[j, ty]
        cuda.syncthreads()
    C[x, y] = tmp

A = numpy.full((TPB * 130, TPB * 130), 3, numpy.float)
B = numpy.full((TPB * 130, TPB * 130), 4, numpy.float)
C_cpu = numpy.full((A.shape[0], B.shape[1]), 0, numpy.float)

print("start processing in CPU")
start_cpu = time.time()
matmul_cpu(A, B, C_cpu)
end_cpu = time.time()
time_cpu = end_cpu - start_cpu
print("CPU time: " + str(time_cpu))

# start in GPU
A_global_mem = cuda.to_device(A)
B_global_mem = cuda.to_device(B)

C_global_mem = cuda.device_array((A.shape[0], B.shape[1]))
C_shared_mem = cuda.device_array((A.shape[0], B.shape[1]))

threads_per_block = (TPB, TPB)
blocks_per_grid_x = int(math.ceil(A.shape[0] / threads_per_block[0]))
blocks_per_grid_y = int(math.ceil(B.shape[1] / threads_per_block[1]))
blocks_per_grid = (blocks_per_grid_x, blocks_per_grid_y)

print("start processing in GPU")
start_gpu = time.time()
matmul_gpu[blocks_per_grid, threads_per_block](A_global_mem, B_global_mem, C_global_mem)
cuda.synchronize()
end_gpu = time.time()
time_gpu = end_gpu - start_gpu
print("GPU time(Global memory):" + str(time_gpu))
C_global_gpu = C_global_mem.copy_to_host()

start_gpu_shared_memory = time.time()
matmul_shared_mem[blocks_per_grid, threads_per_block](A_global_mem, B_global_mem, C_shared_mem)
cuda.synchronize()
end_gpu_shared_memory = time.time()

time_gpu_shared = end_gpu_shared_memory - start_gpu_shared_memory
print("GPU time(shared memory):" + str(time_gpu_shared))
C_shared_gpu = C_global_mem.copy_to_host()

结果展示：

可见GPU加速后的矩阵计算已在速度上遥遥领先，经过共享内存加速的程序也提升了计算性能。基于笔者采用的时GTX 860 4G显存的笔记本GPU设备做的内存加速，所以效果并非特别明显。在一些具有高性能大容量显存的GPU设备上进行内存优化将会获得数倍的性能提升。

参考内容

https://blog.csdn.net/LN_IOS/article/details/80538570
https://info.nvidia.com/364565-ondemand.html
https://images.nvidia.cn/cn/webinars/2020/jun23/CUDA-python%E7%B3%BB%E5%88%97%E8%AF%BE%E7%A8%8B-%E5%B9%B6%E8%A1%8C%E8%AE%A1%E7%AE%97%E5%9F%BA%E7%A1%80%20—%E7%9F%A9%E9%98%B5%E8%AE%A1%E7%AE%97%E4%BB%A5%E5%8F%8A%E5%85%B1%E4%BA%AB%E5%86%85%E5%AD%98.pdf