【深度强化学习】Sarsa

Sarsa

正如其名，SARSA 即是使用 $(s_t,a_t,r_t,s_{t+1},a_{t+1})$ 来更新 $Q_{\pi }$，也就是 State-Action-Reward-State-Action。

1 TD target

首先，我们回顾一下 $\text{discounted return}$：
$$\begin{array}{c}{U}_t=R_t+\gamma \cdot R_{t+1}+{\gamma }^2\cdot R_{t+2}+{\gamma }^3\cdot R_{t+3}+{\gamma }^4\cdot R_{t+4}+\cdots \\ =R_t+\gamma \cdot \left(R_{t+1}+\gamma \cdot R_{t+2}+{\gamma }^2\cdot R_{t+3}+{\gamma }^3\cdot R_{t+4}+\cdots \right)\end{array}$$

也就是 $U_t=R_t+\gamma \cdot U_{t+1}$，该式反应了相邻两个回报之间的关系。

假设 $R_t$ 依赖于 $(S_t,A_t,S_{t+1})$，有下式：
$$\begin{array}{rl}{Q}_{\pi }\left(s_t,a_t\right)& =\mathbb{E}\left[U_t\mid s_t,a_t\right]\\ & =\mathbb{E}\left[R_t+\gamma \cdot U_{t+1}\mid s_t,a_t\right]\\ & =\mathbb{E}\left[R_t\mid s_t,a_t\right]+\gamma \cdot \mathbb{E}\left[U_{t+1}\mid s_t,a_t\right]\\ & =\mathbb{E}\left[R_t\mid s_t,a_t\right]+\gamma \cdot \mathbb{E}\left[Q_{\pi }\left(S_{t+1},A_{t+1}\right)\mid s_t,a_t\right]\end{array}$$

于是我们有: $Q_{\pi }\left(s_t,a_t\right)=\mathbb{E}\left[R_t+\gamma \cdot Q_{\pi }(S_{t+1},A_{t+1})\right]$。这里有对 $，S_{t+1}，A_{t+1}$ 的期望，直接计算很困难，因此可以使用 MC 近似。将 $R_t$ 近似为观测到的奖励 $r_t$，将 $，S_{t+1}，A_{t+1}$ 近似为观测到的 $s_{t+1},a_{t+1}$。于是我们有：
$$Q_{\pi }\left(s_t,a_t\right)=\mathbb{E}\left[R_t+\gamma \cdot Q_{\pi }(S_{t+1},A_{t+1})\right]\approx r_t+\gamma \cdot Q_{\pi }\left(s_{t+1},a_{t+1}\right)$$

把 $r_t+\gamma \cdot Q_{\pi }\left(s_{t+1},a_{t+1}\right)$ 称为 TD target $y_t$。TD target 部分基于真实观测到的奖励，部分基于 $Q_{\pi }$ 做出的预测。

TD learning 就是想 让动作价值 $Q_{\pi }(s_t,a_t)$ 接近 $y_t$，这是因为 $Q_{\pi }$ 完全是估计，而 TD target $y_t$ 部分基于真实观测的奖励。

2 Tabular Version

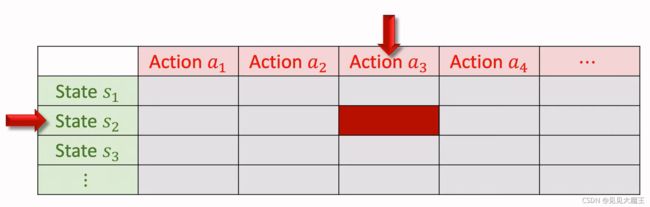
如果状态空间和动作空间都是有限的，我们想要学习 $Q_{\pi }(s,a)$，可使用表格法。表中的每个元素代表一个动作价值。我们要做的就是用 Sarsa 算法更新表格，每次更新一个元素。

算法过程：

1. 观测到一个 transition：$(s_t,a_t,r_t,s_{t+1})$；
2. 使用策略函数 $a_{t+1}\sim \pi \left(\cdot \mid s_{t+1}\right)$ 选择下一个动作 $a_{t+1}$；
3. 计算 TD target：$y_t=r_t+\gamma \cdot Q_{\pi }\left(s_{t+1},a_{t+1}\right)$，其中 $r_t$ 是真实值，$Q_{\pi }\left(s_{t+1},a_{t+1}\right)$ 可通过查表得出；
4. 计算 TD error：${\delta }_t=Q_{\pi }\left(s_t,a_t\right)-y_t$；
5. 最后用 ${\delta }_t$ 去更新动作价值 $Q_{\pi }\left(s_t,a_t\right)$：$Q_{\pi }\left(s_t,a_t\right)\leftarrow Q_{\pi }\left(s_t,a_t\right)-\alpha \cdot {\delta }_t$，其中 $\alpha$ 为学习率。

3 Neural Network Version

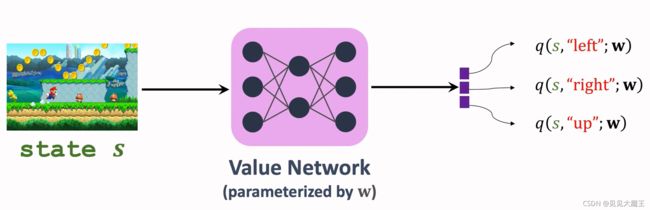
可以使用 value network 来近似动作价值函数 $Q_{\pi }$，把 value network（含参数 $w$）记为函数 $q(s,a;w)$。参数 $w$ 是随机初始化的，根据观测到的奖励来更新 $w$。

这里的 value network 也就是 actor-critic 中的 critic，用来评价 actor。

算法过程：

1. 计算 TD target：$y_t=r_t+\gamma \cdot q\left(s_{t+1},a_{t+1};\mathbf{w}\right)$；
2. 计算 TD error：${\delta }_t=q\left(s_t,a_t;\mathbf{w}\right)-y_t$；
3. 损失函数定义为：${\delta }_t^2/2$；
4. 计算梯度：$\frac{\partial {\delta }_t^2/2}{\partial \mathbf{w}}={\delta }_t\cdot \frac{\partial q\left(s_t,a_t;\mathbf{w}\right)}{\partial \mathbf{w}}$；
5. 根据梯度更新参数 $w$：$\mathbf{w}\leftarrow \mathbf{w}-\alpha \cdot {\delta }_t\cdot \frac{\partial q\left(s_t,a_t;\mathbf{w}\right)}{\partial \mathbf{w}}$。

Summary

1. SARSA 的目标是学习 state-action 值函数 $Q_{\pi }$。
2. 表格法的 SARSA 学习的是 $Q_{\pi }$，使用条件是其动作空间和状态空间是有限集。
3. 价值网络的 SARSA 学习的是动作价值函数 $Q_{\pi }$ 的近似 $q$，每次迭代更新的是近似函数 $q$ 的参数。

Reference

https://www.youtube.com/watch?v=-cYWdUubB6Q&list=PLvOO0btloRnvWZCkAUrBbVB5ZjDI2hUAM