CHIPNET ICLR2021
CHIPNET ICLR2021论文精读
原文链接:link
代码链接:link
本文完全是个人见解,可能有理解错的地方请大家多多包涵,及时指正。
contribution

想法感觉很不错,之前看的大多数剪枝都是先训练然后将权重绝对值最小的那部分按照剪枝比例剪掉,然后迭代剪。
这篇文章将mask变成一个可以使用梯度来更新的量(我看到的文章很少有基于梯度更新mask的,如果大家有看到过类似文章,欢迎在评论区分享)
剪枝mask由0-1构成,是离散的无法使用gradient-based 方法更新mask,本文通过将{0,1}的mask转化为[0,1]的连续函数,从而可以使mask能够使用梯度更新。接下来问题就转化成了如何将[0,1]的数投影到{0,1}
proposed approach
主要以下分为3个函数:
logistic curves
z ~ = 1 1 + e − β ( ψ − ψ 0 ) \widetilde{z}=\frac {1} {1+e^{-\beta(\psi-\psi_{0})}} z =1+e−β(ψ−ψ0)1
不同 β \beta β得到的 z ~ \widetilde{z} z 曲线
当 β \beta β很小时, z ~ \widetilde{z} z 近似一个在-1到1上呈线性的曲线,当 β \beta β很大时, z ~ \widetilde{z} z 近似一个阶跃函数。

continuous Heaviside function
仅仅是logistic curves不能获得离散的{0,1}的值,因此引入了continuous Heaviside function
z = 1 − e − γ z ~ + z ~ e − γ z=1-e^{-\gamma\widetilde{z}}+\widetilde{z}e^{-\gamma} z=1−e−γz +z e−γ
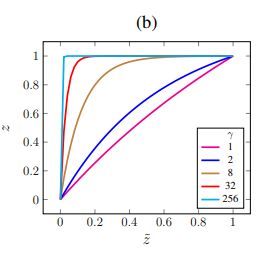
不同 γ \gamma γ得到的 z z z曲线
由下图可以看出, γ = 0 \gamma=0 γ=0时,曲线 z z z是线性的, γ \gamma γ越大,曲线 z z z越接近阶跃函数
crispness loss
虽然logistic curves和continuous Heaviside function有助于获得离散的{0,1}值,但是没有约束或者罚函数来约束它,因此文章中给出了一个crispness loss
L c = ∣ ∣ z ~ − z ∣ ∣ 2 2 \mathcal{L}_c=||\widetilde{z}-z||_2^2 Lc=∣∣z −z∣∣22
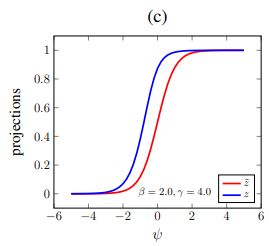
上图是 β = 2 \beta=2 β=2, γ = 4 \gamma=4 γ=4对应的logistic curves和continuous Heaviside function曲线,只有当 z ~ = z = 0 \widetilde{z}=z=0 z =z=0或者 z ~ = z = 1 \widetilde{z}=z=1 z =z=1时 L c \mathcal{L}_c Lc最小,为0。
下图是不同的 β \beta β, γ \gamma γ对应的 L c ( ψ ) \mathcal{L}_c(\psi) Lc(ψ)曲线
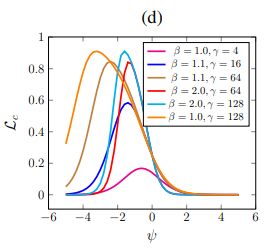
当 β \beta β, γ \gamma γ较小时,crispness loss对剪枝过程影响很小,随着 γ \gamma γ的增加, L c \mathcal{L}_c Lc的尖峰上移且左移,左移使得对于负的 ψ \psi ψ惩罚更大,使其变得更负,这就使得z更接近0。
下图a是所提的方法(包含完整的三部分),b没有crispness loss,c没有without logistic round function,可以看出a的阙值更大,能获得更好的稀疏性。

budget constraints
文中使用了channel, activation volume, parameters and FLOPs这四种开支约束。
文中定义了一项budget loss L b = ( V ( z ) − V 0 ) 2 \mathcal{L}_b=(\mathcal{V}(z)-\mathcal{V}_0)^{2} Lb=(V(z)−V0)2,其中 V ( ⋅ ) \mathcal{V}(\cdot) V(⋅)是上述四种开支之一,在此mark一下,感觉在附录里详细介绍budget constraints的比较少,方便下次查阅。

soft and hard pruning
本文剪枝分为两步:soft pruning 和 hard pruning。预训练模型后应用mask进行软剪枝,软剪枝算法如下图所示:
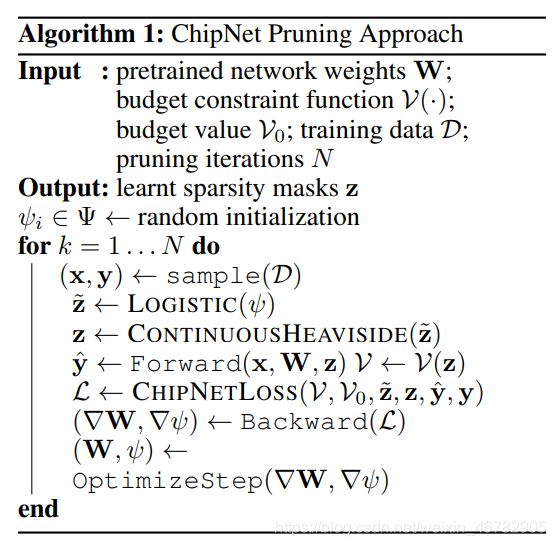
这里的loss由三部分组成: L = L c e + α 1 L c + α 2 L b \mathcal{L}=\mathcal{L}_{ce}+\alpha_{1}\mathcal{L}_{c}+\alpha_{2}\mathcal{L}_{b} L=Lce+α1Lc+α2Lb,这里 L c e \mathcal{L}_{ce} Lce是交叉熵损失。该部分在代码中体现为:
def criterion(model, y_pred, y_true):
global steepness
ce_loss = CE(y_pred, y_true) # orginal loss
budget_loss = ((model.get_remaining(steepness, args.budget_type).to(device) - Vc.to(device)) ** 2).to(device)
crispness_loss = model.get_crispnessLoss(device)
return budget_loss * weightage1 + crispness_loss * weightage2 + ce_loss
在每次软剪枝之后,都会以硬剪枝的方式评估模型的性能。 最后,选择在验证集上具有最佳性能的模型进行微调。
pseudo code
experiment setup
数据集:CIFAR-10/100 和 Tiny ImageNet
模型: WideResNet-26-12,PreResNet-164,ResNet-50 和 ResNet-101
参数设置: α 1 = 10 \alpha_{1}=10 α1=10, α 2 = 30 \alpha_{2}=30 α2=30
其他细节详见附录,不想写了
results
这里只放结果不分析了,虽然这文章没用ImageNet,但是个人感觉附录写的真的详细,不像有些文章…



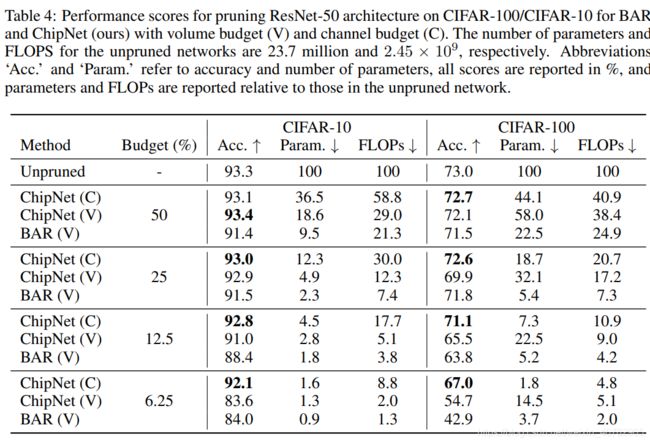

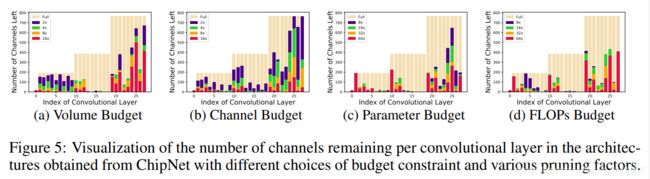
上图可视化感觉有点夸张,中间几层几乎全剪掉了??

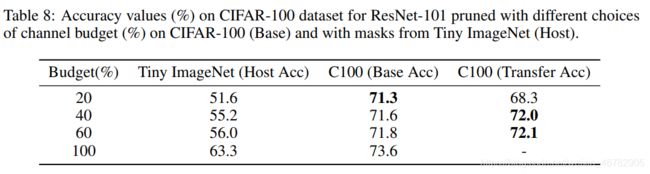
Transfer learning of masks
文章中Tiny ImageNet作为老师模型,CIFAR-100作为学生模型,对ResNet-101进行剪枝,发现当通道开支在40%和60%时,迁移mask的性能比训练原始数据集的更好,可能因为Tiny ImageNet比CIFAR-100信息更加丰富