数据结构与算法（五）—— 栈及其实现和应用

注：本篇内容参考了《Java常用算法手册》、《大话数据结构》和《Java编程（第四版）》三本书籍。

本人水平有限，文中如有错误或其它不妥之处，欢迎大家指正！

 

目录

1. 栈的概述

2. 栈的操作

2.1 入栈(Push)

2.2 出栈(Pop)

2.3 返回栈项(Peek)

3. 进出栈的变化形式

3.1 示例

3.2 规则

4. 栈的存储结构及其实现

4.1 栈的存储结构

4.1.1 顺序存储结构

4.1.2 链式存储结构

4.2 栈的顺序存储结构的实现

4.2.1 栈顺序存储结构的Java实现

4.2.2 顺序栈的共享空间问题

4.3 栈的链式存储结构的实现（基于LinkedList）

5. Java中的栈

6. 栈的作用及应用

6.1 栈的作用

6.2 栈的应用

6.2.1 递归

6.2.2 四则运算

---

 

1. 栈的概述

栈（stack）是限定只能在表尾进行插入和删除操作的线性表。把允许插入和删除操作的一端叫做栈顶（top），另一端叫做栈底（bottom），若栈不包含任何数据则称为空栈。栈按照后进先出（Last In First Out, LIFO）原则处理结点的数据，所以也称为后进先出的线性表，或叠加栈。因为最后压入栈的元素，第一个弹出栈。经常用来类比栈的事物是装有弹弹簧的储放器中的自助餐托盘，最后装入的托盘总是最先拿出来使用的。

栈结构是从数据的运算来分类的，也就是说栈结构具有特殊的运算规则。从数据的逻辑结构来看，栈结构其实就是一种线性结构。栈的元素具有线性关系，即有唯一的前趋和唯一的后继，只不过它是一种特殊的线性表而已。它的特殊之处在于它限制了线性表的插入和删除操作的位置，它始终只在栈顶进行操作。这就使得栈底是固定的，最先进栈的只能在栈底。只有栈顶的元素是可以访问的。

栈与队列的区别是：队列是只允许在一端进行插入操作、而在另一端进行删除操作的线性表。它们都是线性表，区别是栈的插入和删除操作都只能在表尾（栈顶），而队列的插入和删除操作分别在两端。

 

2. 栈的操作

因为栈的插入和删除只能栈顶操作，这样栈的操作就比较简单了。主要有入栈和出栈两种操作。

2.1 入栈(Push)

栈的插入操作（Push）：称为进栈，也叫压栈、入栈。在入栈操作前，先修改栈顶引用，使其向上移出一个元素位置，然后将数据保存到栈顶引用所指向的位置。

2.2 出栈(Pop)

栈的删除操作（Pop）：称为出栈，也叫弹栈，将栈顶的数据弹出。通过修改栈顶引用，使其指向栈中的下一个元素。

2.3 返回栈项(Peek)

返回栈顶元素（peek）：返回栈顶的元素（此操作可以不算），只是返回栈顶，并不移除它，pop会移除它，也可以返回它。

 

 

3. 进出栈的变化形式

3.1 示例

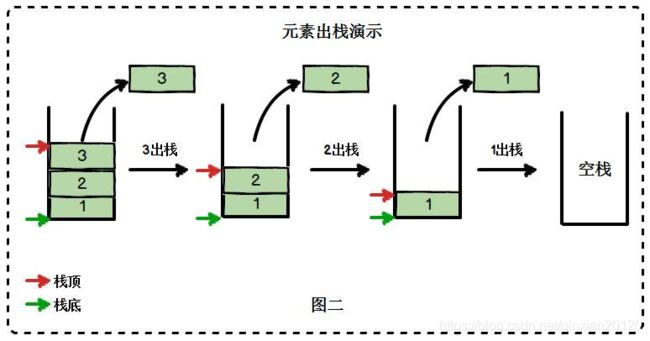
是否最先进栈的元素就只能是最后出栈呢？其实不一定。栈对线性表的插入和删除的位置做了限制，但并没有对元素进出的时间做限制。换句说话，在不是所有元素都进栈的情况下，事先进去的元素也可以出栈，只要保证是从栈顶元素出栈就可以。

举例来说，现有3个整型元素1、2、3依次进栈，会有哪些出栈次序呢？

• 第一种：1、2、3进，3、2、1出，这是最简单也是最好理解的一种，出栈次序为321；
• 第二种：1进，1出，2进，2出，3进，3出。也就是先进一个接着就出来，出栈次序是123；
• 第三种：1进，2进，2出，1出，3进，3出。出栈次序为213；
• 第四种：1进，1出，2进，3进，3出，2出。出栈次序为132；
• 第五种：1进，2进，2出，3进，3出，1出。出栈次序为231。

那有没有312这样的出栈次序呢？肯定不会。因为3先出栈，就意味着3曾经进栈，既然3进栈了，那也意味着1和2已经进栈了，此时2一定是在1的上面，就是2更接近栈顶，那么出栈只可能是321，不然不满足123依次进栈的要求，所以此时不会发生1比2先出栈的情况。

 

3.2 规则

对栈的出栈和进栈，有几条规律（不管入栈的是数字、字母还是其它，按入栈的顺序先从小到大标上数字）：

1. 在原序列中相对位置比它小的，必须是逆序；
2. 在原序列中相对位置比它大的，顺序没有要求；
3. 以上两点可以间插进行。

下面再来看一道题目：一个栈的入栈顺序为ABCDEF，那不可能的出栈序列是哪一项？选 D

A. DEFCBA          B. DCEFBA       C.FEDCBA       D.FECDBA      E.ABCDEF         F.ADCBFE

考的还是栈的先进后出特性，但栈的入栈和出栈顺序是未知的，即出栈的顺序、时机是任意的。ABCDEF入栈，然后FEDCBA出栈，这只是最理想的情况，实际上不一定都是这样的。因为出栈是随机的，很可能是入栈还没结束时就有别的出栈了。在D选项中，F为第一个，也是最大的，那其它出栈的要按逆序，即是F后的后面是EDCBA，显示D项的出栈顺序不是这样的，所以是错的。

 

4. 栈的存储结构及其实现

4.1 栈的存储结构

若从数据的存储结构来进一步划分，栈结构包括顺序存储结构和链式存储结构两类。

4.1.1 顺序存储结构

顺序栈结构：使用一组地址连续的内存单元依次保存栈中的数据。在程序中可定义一个指定大小的结构数组来作为栈，序号为0的元素就是栈底，再定义一个变量top保存栈顶的序号即可。

 

4.1.2 链式存储结构

链式栈结构：使用链表形式保存栈中各元素的值。链表首部(head引用所指向的元素)为栈顶，链表尾部（指向地址为null）为栈底。

在生活中也有类似栈结构的例子，比如放几个一样的物品到一个桶里，最先放进去的会在最底部（以桶底为栈底），放入（理解为插入操作）和取出（理解为删除操作）物品都只能从桶的顶部进行。后放进去的往往是会被先取出消耗或使用。

 

4.2 栈的顺序存储结构的实现

4.2.1 栈顺序存储结构的Java实现

栈的顺序存储其实也是线性表顺序存储的简化，简称为顺序表。线性表是用数组来实现的。试想一下，对于栈这种只能从一头插入和删除的线性表来说，用数组的哪一端来作为栈顶和栈底好呢？

下标为0的一端为栈底比较好，因为首元素都存在栈底，变化量小，所以让它作栈底。定义一个top变量来指标栈顶元素在数组中的位置，栈顶的top可以变大变小，但无论如何都不能超长栈的长度stackSize。当栈存在一个元素时，top等于1，所以通常把空栈的判定条件定为top等于0。

下面通过数组来实现栈。代码如下：

/**
 * @desc    基于数组实现的栈
 * @author  Ethan
 * @version 1.0 
 */

public class ArrayStack {

    /**
     * 默认长度为10
     */
    private static final int DEFAULT_CAPACITY = 20;

    /**
     * 长度
     */
    private int size;

    /**
     * 数组，数组的下标从0开始，所以要在长度的基础上减少1才能对应起来。
     */
    private T[] array;


    /**
     * 构造函数，指定类型
     * @param type
     */
    public ArrayStack (Class type) {
        this(type, DEFAULT_CAPACITY);
    }


    /**
     * 构造函数，指定类型和长度，通过构造函数初始化栈
     * @param type
     * @param size
     */
    public ArrayStack (Class type, int size) {
        array = (T[])Array.newInstance(type, size);
        size = 0;
    }


    /**
     * 是否空栈，是则返回true，否则返回false
     * @return boolean
     */
    public boolean isEmpty () {
        return size() == 0;
    }


    /**
     * 判断是否满栈，是则返回true，否则返回false
     * @return boolean
     */
    public boolean isFull () {
        return size == DEFAULT_CAPACITY;
    }


    /**
     * 返回栈的大小
     * @return
     */
    public int size () {
        return size;
    }


    /**
     * 清空栈
     */
    public void clean () {
        size = 0;
    }


    /**
     * 释放栈
     */
    public void free () {
        if (null != array) {
            array = null;
        }
    }


    /**
     * 入栈：将数据元素保存到栈结构中
     * 具体步骤如下：
     *           1，判断是否满栈，即判断栈顶top是否大于栈的长度，若大于或等于则表示栈满了，抛出异常，拒绝入栈；
     *           2，设置top = top + 1；表示栈顶的引用加1，指向入栈地址；
     *           3，将入栈元素保存到top指向的位置。
     */
    public void push (T val) {
        if (isFull()) {
            throw new RuntimeException("push error, stack is full");
        }
        // 将元素放入栈中
        array[size++] = val;
    }


    /**
     * 出栈：从栈中取出一个元素
     * 具体步骤如下：
     *           1，判断栈顶top是否等于0，若等于0，表示空栈，出栈异常；否则执行下面的步骤；
     *           2，将栈顶的引用top所指向位置的元素返回；
     *           3，设置top=top-1，使栈顶的引用减1，指向栈的下一个元素，原来的栈将被弹出。
     * @return
     */
    public T pop () {
        if (isEmpty()) {
            throw new RuntimeException("pop error, stack is empty");
        }
        T t = array[size-1];
        size --;
        return t;
    }


    /**
     * 返回栈顶元素
     * @return
     */
    public T peek () {
        return array[size-1];
    }


    /**
     * 打印栈的元素内容
     */
    public void print() {
        if (isEmpty()) {
            System.out.println("stack is empty \n");
        }

        System.out.printf("size of stack =%d \n", size);

        int i = size-1;
        while (i >= 0) {
            System.out.println(array[i]);
            i --;
        }
    }
}

下面进行测试。测试代码如下：

public static void main(String[] args) {
        ArrayStack stack = new ArrayStack(String.class);

        // 放入一些数据
        stack.push("a");
        stack.push("b");
        stack.push("c");
        stack.push("d");
        stack.print();

        System.out.println("栈顶元素 :" + stack.peek());

        stack.pop();
        System.out.println();
        System.out.println("-------出栈后的数据-------");
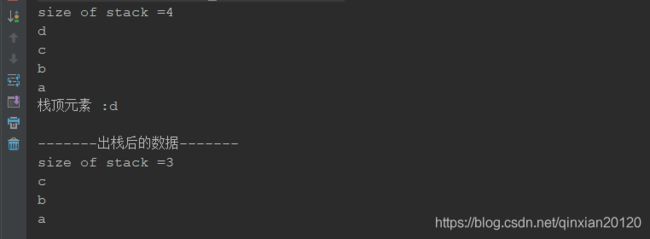
        stack.print();
    }

结果如下：

基于数组实现的栈也有不足，主要在于扩容的问题。不管是默认的大小还是创建时给的大小，在后续都有可能会出现不足的情况。

 

4.2.2 顺序栈的共享空间问题

其实栈的顺序是很方便的，因为它只准栈顶进出元素，所以不存在线性表插入和删除时需要移动元素的问题。但它也有一个很大的缺陷，那就是必须事先确定数组存储空间的大小，万一不够用了，就需要编程手段来扩展数组的容量，非常的麻烦。所以对于一个栈，要尽量考虑周全，设计出合适大小的数组来处理。但对两个相同类型的栈，却可以做到最大限度的利用其事先开辟的存储空间来进行操作。

若我们有两个相同类型的栈，为它们各自开辟了数组空间，极有可能是第一个栈满了，再进栈就溢出了。而另一个栈还有很多存储空间，这就不合理了。我们完全可以一个数组来存储两个栈，但需要一点小技巧。

做法如下图所示。数组有两个端点，两个栈有两个栈底，让一个栈的栈底为数组的始端，即下标为0处，另一个栈的栈底为栈的末端，即下标为n-1处。这样以来，两个栈如果增加元素，就是两端点向中间延伸。

其实关键思路是：它们是在数组的两端向中间靠拢。top1和top2是栈1和栈2的栈顶指针，可以想象，只要它们两个不见面，两个栈就可以一直使用。可以分析出，栈1为空时，就是top1为0；当top2为n-1时，就是栈2为空。那什么时候满栈呢？

想象一下极端的情况，若栈2是空栈，栈1的top1等于n-1时，就是栈1满了。反之，当栈1为空栈时，top2等于0时，栈2就满了。但更多的情况下，其实就是两个栈见面时，也就是两个栈的指针之差为1时，即top1 + 1 = top2为满栈。

 

4.3 栈的链式存储结构的实现（基于LinkedList）

栈的链式存储结构，简称链栈。栈只能在栈顶进行插入和删除操作。有一个问题：栈顶是放在链表的头部还是尾部呢？由于单链表的头结点有地址引用信息，栈顶也是类似，故可以使用单链表来实现。至于双链表什么的，不需要，因为单链表已经可以满足要求了，自然越简单越好。

对于链栈来说，基本没有满栈的情况，除非是内存不够用了。

下面是基于LinkedList实现的栈，代码如下：

import java.util.LinkedList;

/**
 * @desc    基于LinkedList实现的栈
 * @author  Ethan   
 * @version 1.0 
 */

public class LinkedListStack {

    /**
     * 存储器
     */
    private LinkedList storage = new LinkedList<>();


    /**
     * 入栈
     * @param t
     */
    public void push(T t) {
        storage.addFirst(t);
    }


    /**
     * 返回栈顶元素
     * @return
     */
    public T peek() {
        return storage.getFirst();
    }


    /**
     * 出栈
     * @return
     */
    public T pop () {
        return storage.removeFirst();
    }


    /**
     * 是否空栈
     * @return
     */
    public boolean empty() {
        return storage.isEmpty();
    }


    /**
     * 转换成String
     * @return
     */
    @Override
    public String toString() {
        return storage.toString();
    }


    /**
     * 栈的大小
     * @return
     */
    public int size () {
        return storage.size();
    }


    /**
     * 清空栈
     */
    public void clean () {
        storage.clear();
    }
}

下面进行测试，测试代码如下：

  public static void main(String[] args) {
        LinkedListStack stack = new LinkedListStack<>();
        for (String s : "My name is Ethan".split(" ")) {
            stack.push(s);
        }
        System.out.println(stack.peek());
        while (!stack.empty()) {
            System.out.println(stack.pop());
        }
    }

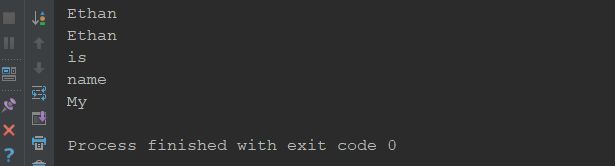
打印结果如下图：

 

5. Java中的栈

在Java中，已经有了栈的实现，在java.util包下，有一个类Stack.class。如下截图，是Stack.class的部分源码：

Java 1.0/1.1的很奇怪，竟然不是用Vector来构建Stack.class，而是选择继承Vector，所以它拥有Vector的特点和行为。再加上一些额外的Stack行为。很难了解设计者是否意识到这样做有特别之处，或者只是一个幼稚的设计。唯一清楚的是，在匆忙发布之前没有经过仔细审查，因此这个糟糕的设计仍然挂在这里，但是永远都不应该去使用它。

在java.util中没有任何公共的Stack接口，这可能是因为在Java 1.0中的设计欠佳的最初的java.util.Stack类占用了这个名字。尽管有了java.util.Stack，但是LinkedList可以产生更好的Stack。

看一下源码，因为继承了Vector，实现起来也比较容易，代码量也不多，加注解不到150行。

 

下面使用java.util.Stack，并测试。测试代码如下：

public static void main(String[] args) {
        Stack stack = new Stack<>();
        for (String s : "My name is Ethan".split(" ")) {
            stack.push(s);
        }
        System.out.println(stack.peek());
        while (!stack.empty()) {
            System.out.println(stack.pop());
        }
    }

上面是测试结果。

在《Java编程思想（第四版）》一书的第11章【持有对象】中提到：“LinkedList具有能够直接实现栈的所有功能的方法，因此可以直接将LinkedList作为栈使用。”

 

6. 栈的作用及应用

6.1 栈的作用

栈的引入简化了程序设计的问题，划分了不同的关注层次，使得思考的范围缩小，有利于聚焦于要解决的问题的核心。像数组，需要考虑下标的问题，初始化数组元素相对麻烦。而且栈的后入先出的特性在不少地方用起来会更好。

 

6.2 栈的应用

栈的内容，描述的也差不多了。那了解学习后有什么呢？下面看下栈的应用。

6.2.1 递归

栈在一个很重要的应用，那就是递归的应用。有一个经典的递归例子：斐波那契数列（Fibonacci），这个例子后面在会在常用和经典的算法一篇中描述。

 

6.2.2 四则运算

另一个重要应用就是做四则运算，就是在做加减乘除运算中会用到。四则运算涉及到顺序和括号的问题，需要先做乘除运算再做加减运算，在做加减时可能是要将几个数一起运算就会用到括号。括号是成对出现的，最终也是完全嵌套匹配的，这时用栈正好合适。只有碰到左括号，就将此左括号进栈，不管表达式有多少重括号，反正遇到左括号就进栈，而后面出现左括号时就让栈顶的左括号出栈，期间让数字运算，这样最好有括号的表达式从左到右巡查一遍，栈应该是由到有元素，最终再因全部匹配成功后成为空栈的结果。

但对四则运算，括号也只是其中的一部分，先乘除后加减使得问题依然复杂，如何有效的处理它们呢？20世纪50年代，波兰科学家Jan Lukasiewicz想到了一种不需要括号的后缀表达法，也把它称为逆波兰（Reverse Polish Nothtion， RPN）表示。这种后缀表示法，是表达式的一种新的显示方式，非常巧妙的解决了程序实现四则运算的难题。

后缀表达式

先来看看，对于“9 + (3 - 1)  ×  3 + 10  ÷ 2”，如果要用后缀表示法应该是什么样子： “9 3 1 — 3 * + 10 2 / +”，这样的表达式称为后缀表达式（在计算机中，数学中的“×” 和“÷”分别用*和/代替）。叫后缀的原因在于所有的符号都是在要运算数字的后面出现。显示这里没有了括号，但对于习惯了数学表达方式的我们来说，这样的表达有点难受，但机器喜欢，比如可爱的计算机。

那计算机是如何应用后缀表达式来计算出结果为20的呢？后缀表达式是：9 3 1 — 3 * + 10 2 / +。规则就是：从左到右遍历表达式的每个数字和符号，遇到是数字就进栈，遇到是符号就将处于栈顶的两个数字出栈，进行运算，再将运算结果进栈，一直到最终获得结果。

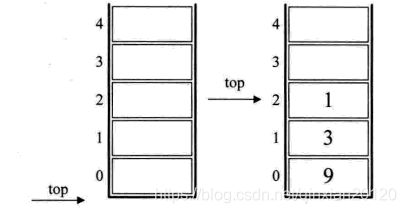
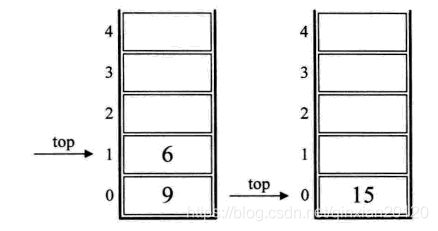
1，初始化一个空栈。此栈用来对要运算的数字进出使用，如下图的左图所示；

2，后缀表达式中前三个都是数字，所以9、3、1进栈，如下图的右图所示；

 

3，接下来是“—”，所以将栈中的1出栈作为减数，3出栈作为被减数，并运算3—1得到2，再将2进栈，如下图的左图所示；

4，接着就是数字3进栈，如下图中的右图所示；

5，后面是“*”，就意味着栈中的3和2出栈，2与3相乘，得到6，并将6进栈，如下图的左图所示；

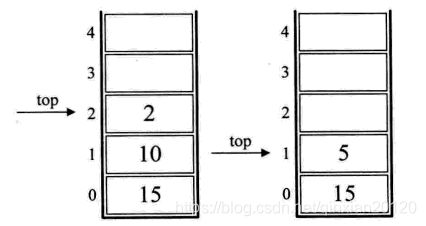
6，下面是“+”，所以栈中的6和9出栈，9与6相加，得到15并进栈，如下图的右图所示；

7，接着是10与2两个数字进栈，如下图的左图所示；

8，接下来是符号“/”，此时栈面的2与10出栈，10与2相除得到5，将5进栈，如下图中的右图所示；

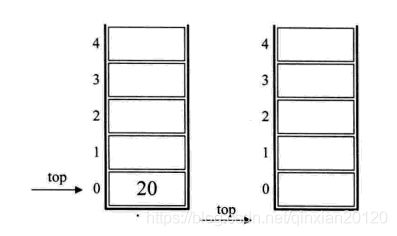
9，最后一个是符号“+”，所以15和5出栈，得到20，将20出栈，如下图的左图所示；

10，结果就是20出栈，栈变为空。如下图的右图所示。

中缀表达式

把平时所用的标准四则运算表达式，即“9 + (3 - 1)  ×  3 + 10  ÷ 2”叫做中缀表达式。因为所有运算符号都在两数字的中间，现在我们的问题就是中缀到后缀的转化。即中缀表达式“9 + (3 - 1)  ×  3 + 10  ÷ 2”转化为后缀表达式“9 3 1 — 3 * + 10 2 / +”。

规则：从左到右遍历中缀表达式的每个数字和符号，若是数字就输出，即成为后缀表达式的一部分；若是符号，则判断其与栈顶符号的优先级，是右括号或优先级低于栈顶符号（乘除优先于加减）则栈顶元素依次出栈并输出，并将当前符号进栈，一直到最终输出后缀表达式为止。

1，初始化—空栈，用来对符号进出栈使用，如下图的左图所示；

2，第一个字符是数字9，输出9，后面是符号“+”，进栈。如下图的右图；

3，第三个字符是“（”，依然是符号，因其只是左括号，还未配对，故进栈，如下图的左图所示；

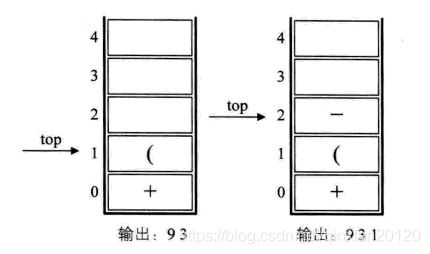
4，第四个字符是数字3，输出，总表达式为9  3，接着是“—”，进栈，如下图的右图所示；

5，接下来是数字1，输出，总表达式是9  3  1，后面是符号“）”，此时需要去匹配此前的“（”，所以栈依次出栈，并输出，直到“（”出栈为止。此时括号上方只有“—”，因此输出“—”。总的输出表达式为9  3  1  —。如下图的左图所示：

6，接着是数字3，输出，总的表达式是9  3  1  —  3。紧接着是符号“×”，因为此时的栈顶符号是“+”号，优先级低于“×”，因此不输出，“*”进栈。如下图的右图所示：

7，之后是符号“+”，此时当前栈顶元素“*”比这个“+”优先级高，因此栈中的元素出栈并输出（没有比“+”号更低的优先级，所以全部出栈），总表达式是9  3  1  —  3  *  +。然后将当前这个符号“+”进栈。即前面几张图的栈低的“+”是指中缀表达式中开头的9后面的那个“+”，而下图的左图中的栈低（也是栈顶）的“+”是指“9+（3-1）×  3 +”中的最一个“+”。

8，紧接着数字10，输出，总的表达式是9  3  1  —  3  *  + 10。后是符号“ ÷”，所以“/”进栈。如下图的右图所示。

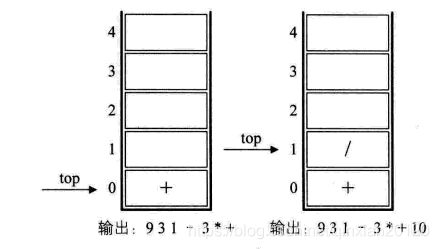
9，最后一个数字2，输出，总的表达式是9  3  1  —  3  *  + 10  2。如下图的左图所示。

10，已到最后了，所以将栈中符号全部出栈并输出。最终输出的后缀表达式结果为9  3  1  —  3  *  + 10  2 /  +。如下图的右图所示。

从上面的推导会发现，要想让计算机具有处理通常的标准（中缀）表达式的能力，最重要的是两步：

1，将中缀表达式转化为后缀表达式（栈用来进出运算的符号）；

2，将后缀表达式进行运算得出结果（栈用来进出运算的数字）。

整个过程都充分利用了栈的后进先出的特性来处理，理解好它其实也就是理解好了栈这个数据结果。