7.7 B树和B+树
2-3树和2-3-4树
内存是由硅制的存储芯片组成,这种技术存储成本比磁盘存储贵很多,因此,目前,磁盘容量很大基本都在1T以上,而内存一般还是8g、16g的水平。内存上处理数据的速度比磁盘处理数据的速度快很多。
大多数数据结构处理数据都在内存中,但是如果我们操作的 数据特别大,内存已经没法处理了,这种情况下对 数据的处理就需要不断从硬盘或u盘这些存储设备中调入或调出内存页面。一旦涉及这样的操作,就 必须考虑对硬盘等外部存储设备的访问时间和访问次数。访问的 次数越多,显然 花费的时间越多,时间复杂度越高,我们 就需要新的数据结构来处理这种问题。
我们先考虑一下树结构,一个结点可以有多个孩子,但是每个结点只能存储一个元素。在元素非常多的时候,要么树的高度非常大,要么树的度特别大(孩子特别多),甚至两者都特别大才行。这样使得内存存取外存次数非常多,这就造成时间效率的瓶颈,因此,我们要打破一个结点只能存储一个元素的限制,这就引出了多路查找树的概念。
多路查找树:每个结点的孩子可以多于两个,且每个结点可以存储多个元素。包括:
- 2-3树
- 2-3-4树
- B树
- B+树
2-3树和2-3-4树都是B树的特例。
1.2-3树的定义
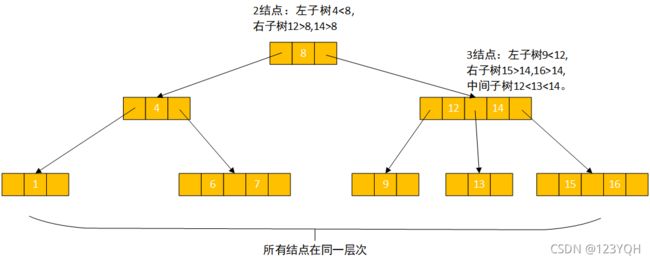
2-3树每个结点都具有两个孩子(称为2结点)或三个孩子(称为3结点):
- 2结点包含一个元素和2个孩子(或没有孩子)。左子树元素小于该元素,右子树元素大于该元素,且2结点要么没有孩子,要么就有2个孩子,不能只有1个孩子。
- 3结点包含一小一大两个元素和3个孩子(或没有孩子),左子树元素小于较小元素,右子树大于较大元素,中间子树介于两元素之间。一个3结点要么没有孩子,要么具有3个孩子。
并且2–3树所有叶子都在同一层上。
如下图的2-3树
2.2-3树的插入
2-3树的插入的原则是:先将这个元素尝试性地插入到已经存在地结点中,如果存放的结点是2结点,那么插入后就会变成3结点;如果要存放地结点是3结点,那么插入后就会变成临时4结点。然后,我们就可能对临时4结点进行分裂处理,使得临时4结点消失。如下图:
2-3树的插入操作分为以下3种情况:
①对于空树,插入一个2结点即可。
②插入结点到一个2结点的叶子上
由于2结点本身只有一个元素,所以只需要将其升级为3结点即可。视插入的元素与当前叶子节点的元素比较后决定谁左谁右。
如:在下图的2-3树种插入元素3,3比1大,所以3在1右边。
③往3结点中插入一个新元素
因为3结点本身已经是2-3树结点最大容量,因此就需将其拆分。主要分为以下几种情况:
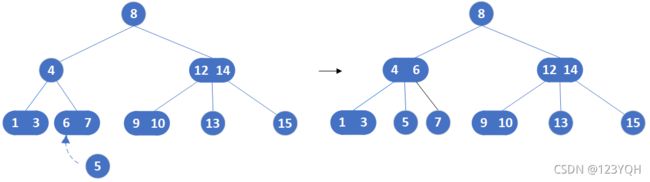
- 双亲是2结点。我们考虑将其变成3结点。
如:插入结点5,应该插在6、7结点的位置,但是6、7元素已经是3结点不能再加。可以发现它的双亲8是2结点,因此考虑让它升级成3结点,将5成为它的中间孩子,让7成为它的右孩子。
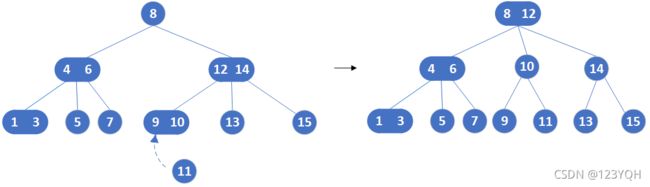
- 双亲也是3结点,但是双亲的双亲是2结点。考虑将双亲的双亲升级成3结点。
如:插入元素11,应该插在9、10元素的3结点位置。但是9、10元素的结点已经是3结点不能再插入元素。可以发现它的双亲12、14结点也是3结点也不能再插入新元素。在网上看,12、14结点的双亲8元素结点是2结点。于是,我们可以将9、10结点拆分,12、14也拆分,让根节点8升级成3结点。
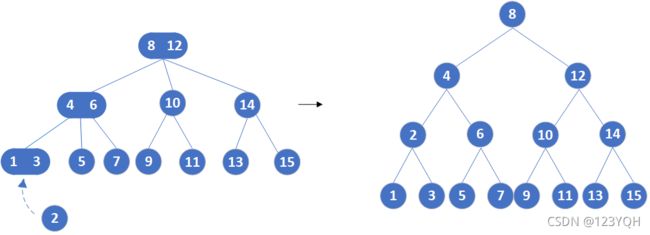
- 祖先都是3结点没有2结点,只能考虑增加树的高度。
如:插入元素2,应该插在1、3结点位置,它的祖先都是3结点不能再增加新元素了,那就意味着树的3层结构不能满足需要,于是将8、12结点,4、6结点,1、3结点拆分,形成下图。
3.2-3树的删除
2-3树的删除操作也分为3种情况。
①删除3结点中的元素。只需要在该节点处删除该元素即可。
如,删除元素9,只需要将3结点改为2结点即可。
**②删除的结点位于一个2结点上,由于2-3树3结点不能有2个孩子,2结点不能只有1个孩子,所以我们不能将2结点直接删除。**分为以下4种情况:
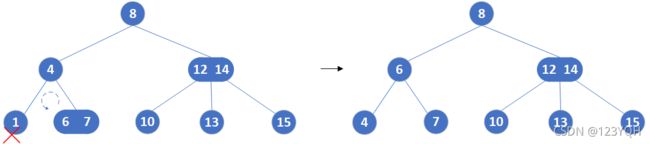
- 此结点的双亲也是一个2结点,且拥有一个3结点的右孩子,那么只需要左旋即可。
如:删除结点1.结点1的双亲是2结点,且有一个3结点的右孩子,左旋得到下图。
- 此结点的双亲是2结点,它的右孩子也是2结点,需要对整棵树变形。
如:删除结点4,此结点双亲是2结点,右孩子也是2结点,如果直接左旋会导致没有右孩子。我们的目标是让结点7变成3结点,然后再左旋,因此让结点9、10的3结点变成2结点,9上去,8下来,得到下中图。然后再左旋即可。
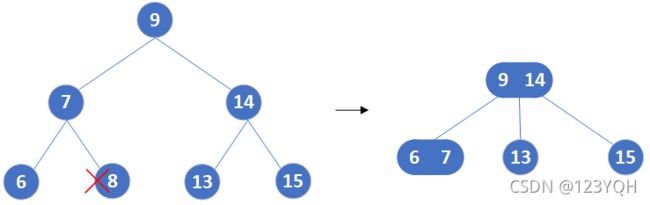
- 如果当前树是一个满二叉树的情况,此时删除任意一个叶子都会使得整棵树不满足2-3树定义。
如:删除结点8,就得考虑将2-3树的层数减少,办法是将8的双亲和左子树6合并成一个3结点,再将14和9合并成3结点。
③删除的元素位于非叶子的分支结点。此时我们通常是将树按中序遍历后得到此元素的前驱或后继元素,考虑让他们补位即可。
如:删除结点12,意味着双亲12、14不能成为3结点,于是将其拆分,并将10和14合并。
4.2-3-4树
在2-3树中插入新元素是由根开始沿着终止于叶子的路径做比较,如果达到的叶子是3结点,并且它已经包含有2个元素,则必须分裂,因为有一个元素要上移一层,则这次分裂就可能导致在叶子之上的结点分裂。因此对2-3树的插入需要从叶子到根的路径上这折返。
如上述的:
在2-4树中,为了避免这种回溯,在从根到叶子的查找过程中,一旦遇到4结点立即分裂。分裂之后当前的处理位置为所沿比较路径下一结点的双亲。
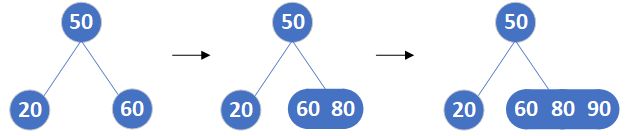
如:插入序列60、50、20、80、90、70、50、10、40、35。
- 插入60、50和20。
- 插入80和90。插入80时,发现根结点是一个4结点,于是分裂这个结点。然后再插入80和90。
- 插入70。**插入70时,发现根的右孩子结点为4结点,将该结点分裂。**然后插入70。
- 插入55、10和40。
- 插入35。查找发现根的左孩子是一个4结点,将该结点分裂。然后插入35。
5.B树
B树是一种平衡的多路查找树。
2-3树和2-3-4树都是它的特例。结点最大的孩子数目称为B树的阶, 因此,2-3树是3阶B树,2-3-4树是4阶B树,B树的插入和删除过程都类似2-3树。
①一棵m阶的B树具有如下属性:
- 如果根节点不是叶结点,则至少有两棵子树。
- 每一个非根的分支结点都有k-1个元素和k个孩子,其中 [m/2]≤k≤m。每一个叶子结点n都有k-1个元素,其中[m/2]≤k≤m。[m/2]表示不小于m/2的最小整数。
- 所有叶子节点都位于同一层次。(不同于AVL树)
- 所有分支节点包含下列信息数据(n,A0,K1,A1,K2,A2,…Kn,An),其中Ki为关键字,且Ki
如:用2-3-4树举例如下,K1
如果我们要查找7,先在外存读取到根节点3、5、8三个元素到内存中,发现7不在当中,通过A2读取外存的6、7结点到内存中,查找到所要元素。
②内存与外存交换数据次数频繁会造成效率瓶颈,B树如何减少次数?
在数据库查询中,以树存储数据,树有多少层,就要访问多少次外存。所以数据量大的时候,用AVL树存的话,高度肯定特别高,因此读取时,要把整个数据读完就要读取外层相当多的次数。这时候用B树,一个结点可以存放多个值,读取时把整个结点读到内存中,在内存中处理速度比外存快得多。
我们外存是将所有信息分割成相等大小的页面,每次硬盘读写的都是一个或多个完整的页面,一页的长度大概21~214B。
在B树的应用中,硬盘数据量很大,因此无法一次全部装入内存。因此我们会对B树进行调整,使得B树的阶数与硬盘存储的页面大小相匹配。比如一棵B树的阶为1001,深度为3,它就可以存储超过10(1000×1000×1000)亿个关键字,我们只要让根结点持久的保留在内存中,那么在这棵树上,寻找某一关键字至多需要两次硬盘的读取即可。
B树就是为了内外存数据交互准备的。
6.B+树
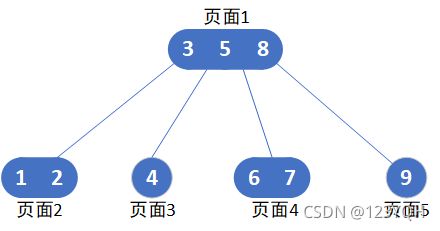
B树虽然有很多好处但是它还是有缺陷的,比如我们想遍历下面这棵B树:
- 先从外存中读取页面2到内存中。遍历1、2。
- 从外存中读取页面1到内存中。遍历3。
- 从外存中读取页面3到内存中。遍历4。
- 从外存中又读取页面1到内存中。遍历5。
- 从外存中读取页面4到内存中。遍历6、7。
- 从外存中再次读取页面1到内存中。遍历8。
- 从外存中读取页面5到内存中。遍历9。
可以看出页面1重复从外存中读取了多次,而且每次遍历页面时都会对页面1的元素进行一次遍历,数据量比较大时效率就会下降很多。
那么我们就要考虑能不能对每一个结点只进行一次遍历?
这就诞生了B+树,一棵m阶B+树和B树的差异在于:
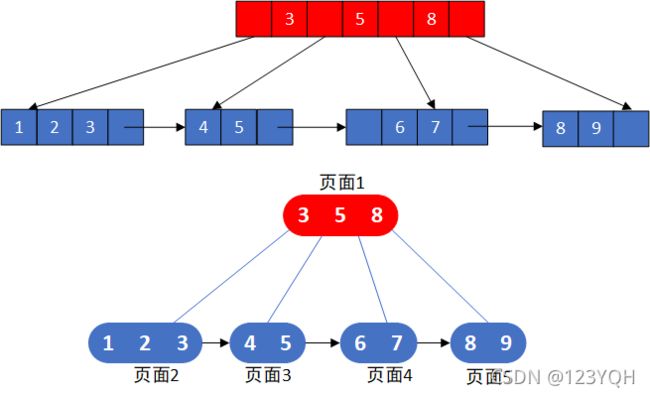
- B+树内部有两种结点,一种是索引结点,一种是叶子结点。
- B+树的索引节点不会保存记录,只用于索引,所有数据都保存在B+树的叶子节点中。而B树则是所有结点都保存数据。
- B+树的叶子节点都会被连成一条链表。叶子本身按索引值的大小从小到大进行排序。即这条链表是从小到大的。多了条链表方便范围查找数据。
- B树的所有索引是不会重复的,而B+树非叶子结点的索引值最终一定会出现在叶子结点中。
如:对上述的B树转变成B+树。其中红色结点表示索引结点,蓝色结点表示
①查找7过程:
- 从外存读取页面1到内存,通过索引发现7在页面4中。
- 从外存读取页面4到内存,遍历得到7。
②中序遍历过程:
- 从外存中读取页面1到内存中,通过索引得到页面2的地址。
- 从外存中读取页面2到内存中。遍历1、2、3。得到页面3的地址。
- 从外存中读取页面3到内存中。遍历4、5。得到页面4的地址。
- 从外存中读取页面4到内存中。遍历6、7、8。得到页面5的地址。
- 从外存中读取页面5到内存中。遍历8、9。
B+树的查找、插入、删除过程与B树类似,但是遍历过程效率提高了很多。
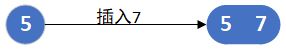






![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-19lElhmV-1638193053425)(C:\Users\ThinkStation K\AppData\Roaming\Typora\typora-user-images\1638192740041.png)]](http://img.e-com-net.com/image/info8/69006e0ab336477e979cc6fac5bf2400.jpg)