BFS模板
void BFS(int s){
queue q;
q.push(s);
while(!q.empty()){
取出队首元素front;
访问队首元素front;
将队首元素出队;
将front的下一层结点中未曾入队的结点全部入队,并设置已入队
}
} DFS模板
递归
priority_queue的cmp函数模板:
struct fruit{
string name;
int price;
}
struct cmp{
bool operator () (fruit f1,fruit f2){
return f1.price > f2.price;
}
}
int main(){
priority_queue,cmp> q;
return 0;
} 中序序列和先序序列、后序序列、层序序列配合重建二叉树的模板:
//记住create函数模板,不管中序和谁配合,模板如下
//postL是后序序列的左端点
//postR是后序序列的右端点
//inL是中序序列的左端点
//inR是中序序列的右端点
//postOrder是后序序列
//inOrder是中序序列
node* create(int postL,int postR,int inL,int inR){
if(postL>postR){
return NULL;
}
int in = postOrder[postR];
node* root = new node;
root->data = in;
int k;
for(k=inL;k<=inR;k++){
if(inOrder[k]==in){
break;
}
}
int numLeft = k-inL;//这一步一定要有
root->lChild = create(postL,postL+numLeft-1,inL,inL+numLeft-1);
root->rChild = create(postL+numLeft,postR-1,inL+numLeft+1,inR);
return root;
}并查集寻找根节点的模板:
//递归写法
int findFather(int n){
if(n==father[n]){
return n;
}
else{
//小括号和中括号要分开
return findFather(father[n]);
}
}并查集合并集合的模板:
void unionS(int a,int b){
int fA = findFather(a);
int fB = findFather(b);
if(fA != fB){
father[fA] = fB;
}
return;
}迪杰斯特拉算法+新增点权+求最短路径条数:
void Dij()
{
//以下三行是初始化工作:
//起点到起点的距离是0;
//起点到起点的最短路径有1条;
//起点到起点累计可以获得的最大资源=该起点本身拥有的资源
d[now] = 0;
shortestNum[now] =1;
maxRescue[now] = cityRescue[now];
//整个for循环中没有用到i的地方,i只用来计数
for(int i=0; i d[u]+roadLen)
{
d[number] = d[u]+roadLen;
shortestNum[number] = shortestNum[u];
//如果最短路径变了,那么累计获得的最大资源要无条件改变
maxRescue[number] = maxRescue[u]+cityRescue[number];
}
else if(d[number]==d[u]+roadLen)
{
shortestNum[number] += shortestNum[u];
//如果最短路径没变,那么累计获得的最大资源要有条件改变
if(maxRescue[u]+cityRescue[number]>maxRescue[number]){
maxRescue[number] = maxRescue[u]+cityRescue[number];
}
}
}
}
}
} 弗罗伊德算法模板
void Floyed()
{
for(int k=0; k普里姆算法模板
//G为图,一般设置成全局变量;数组d为顶点与集合S的最短距离
Prime(G,d[]){
初始化;
for(循环n次){
u = 使d[u]最小的还未被访问的顶点的标号;
记u已被访问;
for(从u出发能到达的所有顶点v){
if(v未被访问 && 以u为中介点使得v与集合S的最短距离d[v]更优){
将G[u][v]赋值给v与集合S的最短距离d[v];
}
}
}
}求素数模板
//给定一个数,判断它是不是素数
#include
#include
#include
using namespace std;
//核心代码
bool isPrime(int n){
if(n<=1){
return false;
}
int a = (int)sqrt(1.0*n);//向下取整
for(int i=2; i<=a; i++){
if(n%i==0){
return false;
}
}
return true;
}
int main()
{
int n;
scanf("%d",&n);
bool is = isPrime(n);
if(is){
printf("Yes");
}
else{
printf("No");
}
return 0;
}
求素数表模板(埃氏筛法)
//求1到n之间的所有素数,
#include
#include
using namespace std;
const int maxn = 1000;
bool is[maxn] = {false};
int prime[maxn];
int p=0;
int n;
//核心代码
void findPrime(){
for(int i=2;i<=n;i++){
if(!is[i]){
prime[p] = i;
p++;
for(int j=i+i;j<=n;j = j+i){
is[j] = true;
}
}
}
}
int main()
{
scanf("%d",&n);
findPrime();
for(int i=0; i 求解最大公约数的模板
//给定两个数n和m,求n和m的最大公约数a
#include
#include
using namespace std;
//核心代码;不必关心a和b的大小,默认a>b,就算ab
int gcd(int a,int b){
if(b==0){
return a;
}
else{
return gcd(b,a%b);
}
}
int main()
{
int n;
int m;
scanf("%d%d",&n,&m);
int a = gcd(n,m);
printf("%d",a);
return 0;
}
求解最小公倍数的模板
//给定两个数n和m,求n和m的最小公倍数b
#include
#include
using namespace std;
//核心代码
int gcd(int a,int b){
if(b==0){
return a;
}
else{
return gcd(b,a%b);
}
}
int main()
{
int n;
int m;
scanf("%d%d",&n,&m);
int a = gcd(n,m);
int b = (n/a)*m;//先求最大公约数,然后再求最小公倍数
printf("%d",b);
return 0;
}
求斐波拉契数列模板(动态规划方法)
一个问题能用动态规划方法求解,需要满足以下两个条件:
- 存在重叠子问题。
- 存在最优子结构(全局问题的最优解可以由局部问题的最优解构成)
//n为45的时候,F(n)就已经有10位数了,超过45的时候,就超过int的极限了,而int是有符号数,符号位发生了改变
#include
#include
using namespace std;
const int maxn = 1000;
int dp[maxn];
//核心代码
int F(int n){
if(n==0 || n==1){
return 1;
}
//这一步让计算复杂度降低很多
else if(dp[n]!=-1){
return dp[n];
}
else{
dp[n] = F(n-1)+F(n-2);
return dp[n];
}
}
int main()
{
for(int i=0; i sort函数
使用sort函数前,进行如下声明:
#include
using namespace std; sort(首元素地址(必填),尾元素地址的下一个地址(必填),比较函数(非必填))
#include
#include
#include
using namespace std;
const double pi = acos(-1.0);
const double eps = 1e-8;
#define EQU(a,b) (fabs((a)-(b))eps)
#define LESS(a,b) (((a)-(b))<(-eps))
#define GREATER_EQU(a,b) (((a)-(b))>(-eps))
#define LESS_EQU(a,b) (((a)-(b))<(eps))
struct node{
int id;
string name;
double grade;
}tmp[3];
bool cmp2(node a,node b){
if(EQU(a.grade,b.grade)){
//成绩相同时按照字典序排列
return a.name >b.name;
}
else{
//成绩高的在前面
return GREATER(a.grade,b.grade);
}
}
bool cmp(double a,double b){
return a>b;
}
int main() {
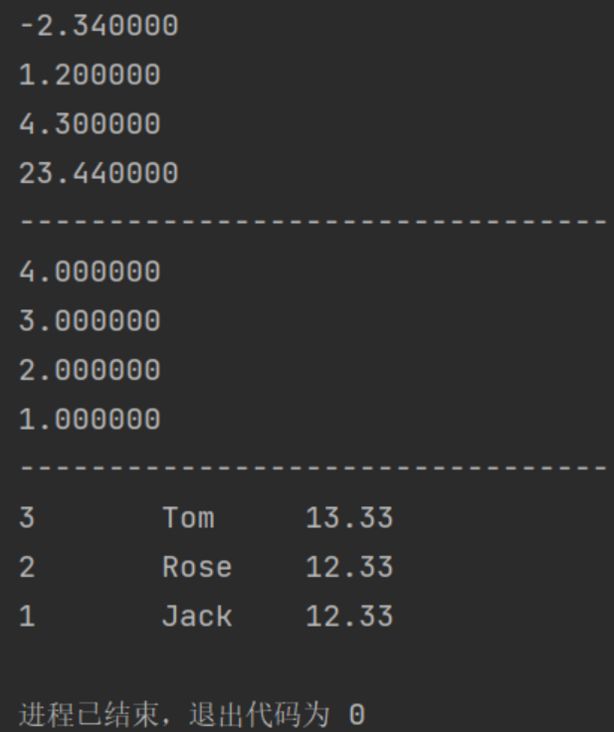
double a[] = {1.2,4.3,-2.34,23.44};
sort(a,a+3);
for(int i=0; i<4; i++){
printf("%lf\n",a[i]);
}
printf("---------------------------------\n");
double b[] = {1.0,2.0,3.0,4.0};
sort(b,b+4,cmp);
for(int i=0; i<4; i++){
printf("%lf\n",b[i]);
}
printf("---------------------------------\n");
tmp[0].grade=12.33;
tmp[0].id=1;
tmp[0].name="Jack";
tmp[1].grade=12.33;
tmp[1].id=2;
tmp[1].name="Rose";
tmp[2].grade=13.33;
tmp[2].id=3;
tmp[2].name="Tom";
sort(tmp,tmp+3,cmp2);
for(int i=0; i<3; i++){
printf("%d\t%s\t%.2f\n",tmp[i].id,tmp[i].name.c_str(),tmp[i].grade);
}
return 0;
}
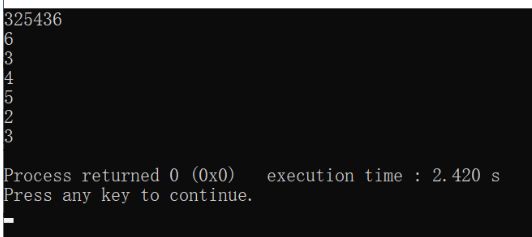
priority_queue中自定义优先级
#include
#include
using namespace std;
struct fruit{
string name;
int price;
friend bool operator < (fruit f1,fruit f2){
return f1.price>f2.price;
}
}f1,f2,f3;
int main() {
priority_queue q;
f1.name = "taozi";
f1.price = 3;
f2.name = "lizi";
f2.price = 4;
f3.name = "pingguo";
f3.price = 1;
q.push(f1);
q.push(f2);
q.push(f3);
cout< 将string类型变量转化为int、long、float、double型变量
C语言转换形式:
std::string str;
int i = atoi(str.c_str());C++转换形式(C++11):
std::string str;
int i = std::stoi(str);同样, 可以使用 stol(long), stof(float), stod(double) 等.
将int、long、float、double型变量转化为string类型变量
to_string( )函数方法是C++11新增的对数字转为字符串string类对象的新功能,主要函数接口如下:
std::to_string
C++ Strings library std::basic_string Defined in header
std::string to_string( int value );
std::string to_string( long value );
std::string to_string( long long value );
std::string to_string( unsigned value );
std::string to_string( unsigned long value );
std::string to_string( unsigned long long value );
std::string to_string( float value );
std::string to_string( double value );
std::string to_string( long double value ); 功能真的很强大而且也很方便。使用如下:
#include
#include
using namespace std;
string str = to_String(123405); 将单个字符char转化为string
使用push_back()
char c = 'a';
string s1;
s1.push_back(c);更多方法:
const char c = 'a';
//1.使用 string 的构造函数
string s(1,c);
//2.声明string 后将char push_back
string s1;
s1.push_back(c);
//3.使用stringstream
stringstream ss;
ss << c;
string str2 = ss.str();
//注意 使用to_string 方法会转化为char对应的ascii码,原因是 to_string 没有接受char型参数的函数原型,
//有一个参数类型为int的函数原型,所以传入char型字符,实际是先将char转化为int型的ascii码,然后再转变为
//string,以下输出结果为97
cout << to_string(c) << endl;将单个字符string转化为char
使用c_str()将string转化为char数组,这个数组其实只有一个元素,就是我们要的char元素
string f = "m";
const char *g1 = f.c_str();
printf("%s\n",g1);数字字符和数字的互相转换
//对于1位数字而言,其整数形式和字符形式差一个'0'
#include
#include
using namespace std;
int main()
{
//字符变数字
char a='3';
int b = a-'0';
int c = b+2;
printf("%d\n",c);
//数字变字符
int d = 6;
char e = d+'0';
printf("%c\n",e);
return 0;
}
小写字母和大写字母的互相转换
//小写字母比大写字母大32
#include
#include
using namespace std;
int main()
{
char a = 'A';
printf("%c\n",a+32);
char b = 'g';
printf("%c\n",b-32);
return 0;
}
将int型数组转换为int型整数
//用户指定输入a位数,然后输入a位数,形成int型数组,然后将int型数组转化为int型整数
#include
#include
using namespace std;
const int maxn = 1000;
int num[maxn];
int a;
int toInt(){
int sum = 0;
for(int i=0; i 将int型整数转换为int型数组
写下面这段代码时得到一个教训:
全局变量和局部变量不能同名,否则会出现无法发现的错误
#include
#include
#include
using namespace std;
const int maxn = 1000;
int n;
int num[maxn];
int k=0;
//核心代码
void toArray(){
for(int i=0; i=pow(10,k)){
k++;
}
toArray();
for(int i=0; i sscanf和sprintf模板
作用是实现字符串和数字的转换。
sscanf和sprintf均在stdio.h头文件下。
scanf("%d",&n);
printf("%d",n);可以写成下面的样子,screen代表屏幕:
scanf(screen,"%d",&n);//将屏幕上用户输入的字符串写到n里(自左向右)
printf(screen,"%d",n);//将n的内容以字符串的形式显示在屏幕上(自右向左)把screen换成字符数组str,就是sscanf和sprintf的用法:
sscanf(str,"%d",&n);//将str中的内容写到n里(自左向右)
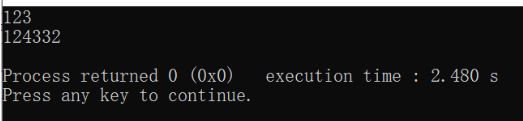
sprintf(str,"%d",n);//将n的内容以字符串的形式写到str上(自右向左)典型应用如下:
#include
#include
using namespace std;
int main()
{
char str[10] = "123";
int a;
sscanf(str,"%d",&a);//将字符串转化为数字
printf("%d\n",a);
int b = 124332;
char stt[20];
sprintf(stt,"%d",b);//将数字转化为字符串
printf("%s\n",stt);
return 0;
}
高级应用如下:
先修知识1:
读入double型变量的语法:
double a;
scanf("%lf",&a);输出double型变量的语法:
printf("%f",a);或者
printf("%.2f",a);先修知识2:
初始化字符数组的方法:
char str[100]= "123a";
//注释中为错误写法
//char str[100];
//str= "123a";
//注释中为错误写法
//char str[100];
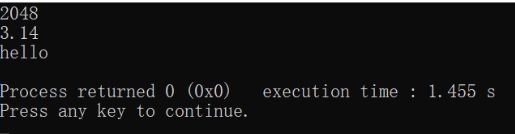
//str[100]= "123a";正式应用1:
#include
#include
using namespace std;
int main()
{
int n;
double db;
char str[100] = "2048:3.14,hello";//初始化字符数组的方法
char str2[100];
sscanf(str,"%d:%lf,%s",&n,&db,str2);//读入double型变量的语法:
printf("%d\n",n);
printf("%.2f\n",db);
printf("%s\n",str2);
return 0;
}
正式应用2:
#include
#include
using namespace std;
int main()
{
int n=12;
double db = 3.1415;
char str[100];
char str2[100] = "good";
sprintf(str,"%d:%.2f,%s",n,db,str2);
printf("%s",str);
return 0;
}
圆周率与浮点数比较
浮点数在计算机中的存储并不总是精确的,需要引入一个极小数eps对这种误差进行修正,eps一般取1e-8
#include
#include
#include
using namespace std;
const double eps = 1e-8;
const double Pi = acos(-1.0);
//注意,Equ后面要跟小括号
#define Equ(a,b) ((fabs((a)-(b)))<(eps))
#define More(a,b) (((a)-(b))>(eps))
#define Less(a,b) (((a)-(b))<(eps))
#define MoreEqu(a,b) (((a)-(b))>(-eps))
#define LessEqu(a,b) (((a)-(b))<(eps))
int main()
{
cout << "Hello world!" << endl;
return 0;
}
读入未知个数的string类型字符串
#include
#include
#include
#include
using namespace std;
int main()
{
string str;
vector now;
//getline(cin,str)!=NULL和getline(cin,str)!=-1都是错的
while(getline(cin,str)){
now.push_back(str);
}
int len = now.size();
for(int i=0; i 获得单链表从后往前第k位
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* getKthFromEnd(ListNode* head, int k) {
int now[5002];
int i=0;
while(head->next != NULL){
now[i] = head->val;
i++;
head = head->next;
}
i = i-2;
ListNode* tmp;
tmp = head;
while(i>=0){
ListNode* a = new ListNode(now[i]);
tmp->next = a;
tmp = a;
i--;
}
return head;
}
};参考书目:《算法笔记》