![]()
更多精彩内容,欢迎关注公众号:数量技术宅,也可添加技术宅个人微信号:sljsz01,与我交流。
Black-Scholes 将期权价格描述为标的价格、行权价、无风险利率、到期时间和波动性的函数。
在本文中,我们使用的波动率值是对未来已实现价格波动率的估计。
鉴于股票价格、行权价、无风险利率和到期时间都是已知且容易找到的,我们实际上可以将市场上的期权价格视为 σ 的函数。
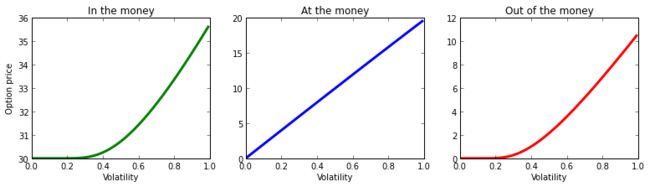
期权的价格在 σ 中单调增加,这意味着随着波动性的增加,期权的价值也会增加,如下图所示。
当价格等于期权行权价时,其结果是线性的(中间图)。而当行权价高于或低于当前价格时(左右图),波动性的增加也会对期权价格产生积极影响。
寻找市场隐含波动率
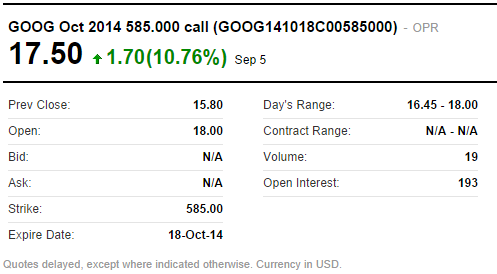
以下是 GOOG 的看涨期权报价,其行使价为 585.00,到期日为 2014 年 10 月 18 日。最后交易价格为 17.50 美元。
从目前收集到的数据中,我们可以看到:
V=BS(S,K,r,T,σ)
$17.50=BS(586.08,585.00,0.0002,0.10958....,σ)
虽然上述方法可行,但它相当不精确。 我们可以做的是使用求根方法,如二分法或牛顿法。
牛顿法
牛顿法是一种寻找函数根的提高近似值的方法。通过隐含波动率,我们试图找出使我们的期权价格尽可能接近 8.50 美元的 σ 值。
这里,我们的 f(x) 函数是期权定价的 Black-Scholes 方程:
Vmodel=f(x)=BS(σ)
那么让我们在python中实现牛顿的方法:
def find_vol(target_value, call_put, S, K, T, r):
MAX_ITERATIONS = 100
PRECISION = 1.0e-5
sigma = 0.5
for i in xrange(0, MAX_ITERATIONS):
price = bs_price(call_put, S, K, T, r, sigma)
vega = bs_vega(call_put, S, K, T, r, sigma)
price = price
diff = target_value - price # 我们的根
print i, sigma, diff
if (abs(diff) < PRECISION):
return sigma
sigma = sigma + diff/vega # f(x) / f'(x)
# 未找到值,返回迄今为止的最佳猜测
return sigma
这里,我们将精度设置为 1e-5 (0.00001),并且我们不会执行超过 100 次的猜测。
我们还需要两个计算Black-Scholes公式的函数,bs_price 和 bs_vega:
n = norm.pdf
N = norm.cdf
def bs_price(cp_flag,S,K,T,r,v,q=0.0):
d1 = (log(S/K)+(r+v*v/2.)*T)/(v*sqrt(T))
d2 = d1-v*sqrt(T)
if cp_flag == 'c':
price = S*exp(-q*T)*N(d1)-K*exp(-r*T)*N(d2)
else:
price = K*exp(-r*T)*N(-d2)-S*exp(-q*T)*N(-d1)
return price
def bs_vega(cp_flag,S,K,T,r,v,q=0.0):
d1 = (log(S/K)+(r+v*v/2.)*T)/(v*sqrt(T))
return S * sqrt(T)*n(d1)
让我们尝试找出上面报价的隐含波动率:
V_market = 17.5
K = 585
T = (datetime.date(2014,10,18) - datetime.date(2014,9,8)).days / 365.
S = 586.08
r = 0.0002
cp = 'c' # 看涨期权
implied_vol = find_vol(V_market, cp, S, K, T, r)
print 'Implied vol: %.2f%%' % (implied_vol * 100)
print 'Market price = %.2f' % V_market
print 'Model price = %.2f' % bs_price(cp, S, K, T, r, implied_vol)
运行Python代码,得到结果:
Implied vol: 21.92%
Market price = 17.50
Model price = 17.50
到这里,我们已经成功计算了上述期权的隐含波动率。 2014 年 10 月 18 日到期的 585 美元看涨期权的隐含波动率为 21.92%。
![]()
![]()
往期干货分享推荐阅读
数字货币稳定币对网格做市策略
数字货币资金费策略
分享一个年化15%以上的无风险套利机会
网格交易系统开发
通过深度学习股价截面数据分析和预测股票价格
Omega System Trading and Development Club内部分享策略Easylanguage源码
一个真实数据集的完整机器学习解决方案(下)
一个真实数据集的完整机器学习解决方案(上)
如何使用交易开拓者(TB)开发数字货币策略
股指期货高频数据机器学习预测
如何使用TradingView(TV)回测数字货币交易策略
如何投资股票型基金?什么时间买?买什么?
【数量技术宅|量化投资策略系列分享】基于指数移动平均的股指期货交易策略
AMA指标原作者Perry Kaufman 100+套交易策略源码分享
【 数量技术宅 | 期权系列分享】期权策略的“独孤九剑”
【数量技术宅|金融数据系列分享】套利策略的价差序列计算,恐怕没有你想的那么简单
【数量技术宅|量化投资策略系列分享】成熟交易者期货持仓跟随策略
如何获取免费的数字货币历史数据
【数量技术宅|量化投资策略系列分享】多周期共振交易策略
【数量技术宅|金融数据分析系列分享】为什么中证500(IC)是最适合长期做多的指数
商品现货数据不好拿?商品季节性难跟踪?一键解决没烦恼的Python爬虫分享
【数量技术宅|金融数据分析系列分享】如何正确抄底商品期货、大宗商品
【数量技术宅|量化投资策略系列分享】股指期货IF分钟波动率统计策略
【数量技术宅 | Python爬虫系列分享】实时监控股市重大公告的Python爬虫