卡尔曼滤波器

卡尔曼滤波器的前言

首先，介绍条件概率。
思考这一个问题：在一个学校里面，学生里面的男生占比0.6，女生占比0.4，男生留长发的概率是0.2，男生短发的概率是0.8，女生留长发的概率是0.9，女生短发的概率是0.1，现在你从背影看到一个留长发的人，判断他（她）是男生还是女生？
$$P(s=男生)=0.6P(s=女生)=0.4$$

$$\begin{gathered} P(o=短发|s=男生)=0.8P(o=长发|s=男生)=0.2 \\ P(o=短发|s=女生)=0.1P(o=长发|s=女生)=0.9 \end{gathered}$$

那么
$$P(s=男生|o=长发)=\frac{P(s=男生,o=长发)}{P(o=长发)}=\frac{P(o=长发|s=男生)P(s=男生)}{P(o=长发|s=男生)P(s=男生)+P(o=长发|s=女生)P(s=女生)}=\frac{0.2\times 0.6}{0.2\times 0.6+0.9\times 0.4}=0.25$$

$$P(s=女生|o=长发)=\frac{P(s=女生,o=长发)}{P(o=长发)}=\frac{P(o=长发|s=女生)P(s=女生)}{P(o=长发|s=男生)P(s=男生)+P(o=长发|s=女生)P(s=女生)}=\frac{0.9\times 0.4}{0.2\times 0.6+0.9\times 0.4}=0.75$$
所以，当看到背影是长发的同学，是女生的概率更大一些，有0.75，所以我们猜测这是个女生。
PS：根据上边这个例子，直观点的解释如下。
假设这个学校有1000个学生，按照上面的概率，那么男生约600人，女生约400人，留长发的女生约360人，留短发的女生约40人，留长发的男生约120人，留短发的男生约480人。当看到一个背影长发的同学，这个同学肯定从长发男生和长发女生这个总体选出来的一个，长发群体总共480人（男生120人，女生360人），那么我们肯定推断这个选出来的背影是长发的同学肯定是女生的概率更大。

下面对这个例子作一些补充，其中$s$为隐状态，意思是我们不能直观看到，$o$是观测量，是我们我可以直观看到的。就像上面的例子一样，同学的真实性别我们观测不到，是隐状态，但是我们可以根据背影看到是否为长发，是否为长发就是观测量。

下面给出卡尔曼滤波器的两个式子，
$$x_k=A{x}_{k-1}+B{u}_{k-1}+w_{k-1}$$
上式是系统的状态方程，其中$x_k$是系统在$k$时刻的系统状态量，$x_k:n\times 1$，$x_{k-1}$是系统在$k-1$时刻的系统状态量，$x_{k-1}:n\times 1$，$A$是系统矩阵，$A:n\times n$，$B$是输入矩阵（也叫控制矩阵），$B:n\times r$，$u_{k-1}$是系统在$k-1$时刻的系统输入，$u_{k-1}:r\times 1$，$w_{k-1}$是服从高斯分布的随机向量，相当于是系统噪声，$w_{k-1}:n\times 1$，$w_{k-1}\sim N_p(0,Q)$，$Q$是系统噪声服从的协方差矩阵，$Q:n\times n$。
$$y_k=H{x}_k+v_k$$
上式是系统的观测方程，其中$x_k$是系统在$k$时刻的系统状态量，$x_k:n\times 1$，$H$是系统状态到观测值（系统中的传感器数据）的转换矩阵，$H:m\times n$,$v_k$是测量噪声，$v_k:m\times 1$，$v_k\sim N_p(0,R)$，$R$是测量噪声服从的协方差矩阵，$R:m\times m$，$y_k$是系统的观测值（系统中的传感器数据）。
与上面举的学校男女生的例子类比，系统的状态量$x_k$是我们直接观测不到的，即隐状态，我们能观测到的量是传感器的数据$y_k$，现在我们要推算$k$时刻系统中的真实状态值$x_k$，在推测$x_k$的同时，我们已经知道系统过往的测量值$y_1,y_2,\dots ,y_k$，系统过往的真实状态值$x_1,x_2,\dots ,x_{k-1}$我们是不知道的，即使我们对$x_1,x_2,\dots ,x_{k-1}$做出了估计。为了更好的展示该过程的逻辑，如下图所示，

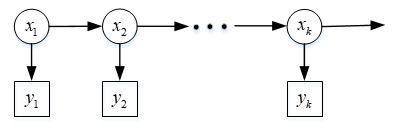
如上图所示，系统的真实状态随着时间逐渐变化，在时间步$k$对应观测向量$y_k$（可能系统有多个传感器，所以每一次可以得到一个观测向量）。重点来了！！！现在，需要要做的是，在已知系统过往的观测值向量$y_1,y_2,\dots ,y_{k-1}$和当前观测值向量$y_k$的前提下，估计当前状态$x_k$最可能取到的值，其数学表达式为
$${\hat{x}}_k=\text{argmax}P(x_k|y_1,y_2,\dots ,y_k)$$
这里举个例子，帮助理解上式，如果$P(x_k|y_1,y_2,\dots ,y_k)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{\frac{-(x_k-\mu {)}^2}{2{\sigma }^2}}$，那么让我们估计一下$x_k$的值，我们肯定将估计值${\hat{x}}_k$取$\mu$，因为在$x_k=\mu$发生的概率最大。其实卡尔曼滤波就做了这件事，计算出$k$时刻的$P(x_k|y_1,y_2,\dots ,y_k)$，这个式子是多元正态分布（为什么呢？下面我就介绍），先说一下，多元正态分布表达式的一般形式，如下所示，
$$f(x)=\frac{1}{(\sqrt{2\pi }{)}^p|\Sigma {|}^{\frac{1}{2}}}{e}^{-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )}$$
其中，$x$是随机向量，$x:p\times 1$,$\Sigma$是随机向量$x$的协方差矩阵，$\Sigma :p\times p$，$\mu$是随机向量$x$的均值，$\mu :p\times 1$，$f(x)$也称为随机向量$x$的概率密度函数，也记作$x\sim N_p(\mu ,\Sigma )$。

卡尔曼滤波器的推导

首先，为了便于阅读，我把系统的状态方程和观测方程和系统中状态转移图放在这里，每个量的含义都在上文有解释，这里不再赘述。
$$x_k=A{x}_{k-1}+B{u}_{k-1}+w_{k-1}$$

$$y_k=H{x}_k+v_k$$

首先，假设我们这个系统是个电阻电容系统，在时间$t=1$时，系统刚上电，此时系统中的观测值为$y_1$，在观测值$y_1$发生的前提下，我们假设
$$P(x_1|y_1)\sim N_n({\hat{\mu }}_1,{\hat{\Sigma }}_1)$$
事实上，这个是我们必须做出的假设，假设中的参数也容易写，因为系统刚上电，${\hat{\mu }}_1$直接取作系统的初始状态值就行了，因为系统中是存在不确定性（噪声），如果噪声很小，我们${\hat{\Sigma }}_1$就可以方差取小一些，反之，取大一些。这个算是，我们使用卡尔曼滤波器的一个超参数，是需要我们提前做出假设的。PS：肯定有人会问，如果我们开始这个假设和系统真实情况$P(x_1|y_1)$不太符合怎么办，其实问题不大，后面再迭代过程中，这个初始假设中存在的不合理性，会慢慢弱化。后面仿真，会对这个初始假设做进一步说明。

然后，在时间$t=2$的时候，我们需要计算$P(x_2|y_1,y_2)$。

根据数学归纳法，假设$t=k-1$时，$P(x_{k-1}|y_1,y_2,\dots ,y_{k-1})\sim N_n({\hat{\mu }}_{k-1},{\hat{\Sigma }}_{k-1})$，在$t=k$时，
$$P(x_k|y_1,y_2,\dots ,y_k)=\frac{P(x_k,y_k|y_1,y_2,\dots ,y_{k-1})}{P(y_k|y_1,y_2,\dots ,y_{k-1})}$$
因为$P(x_{k-1}|y_1,y_2,\dots ,y_{k-1})\sim N_n({\hat{\mu }}_{k-1},{\hat{\Sigma }}_{k-1})$，且$x_k=A{x}_{k-1}+B{u}_{k-1}+w_{k-1}$，则有
$$P(x_k|y_1,y_2,\dots ,y_{k-1})\sim N_n(A{\hat{\mu }}_{k-1}+B{u}_{k-1},A{\hat{\Sigma }}_{k-1}{A}^T+Q)$$

因为$P(x_k|y_1,y_2,\dots ,y_{k-1})\sim N_n(A{\hat{\mu }}_{k-1}+B{u}_{k-1},A{\hat{\Sigma }}_{k-1}{A}^T+Q)$，且$y_k=H{x}_k+v_k$，则有
$$P(y_k|y_1,y_2,\dots ,y_{k-1})\sim N_n(H(A{\hat{\mu }}_{k-1}+B{u}_{k-1}),H(A{\hat{\Sigma }}_{k-1}{A}^T+Q)H^T+R)$$
因为$P(x_k|y_1,y_2,\dots ,y_{k-1})$和$P(y_k|y_1,y_2,\dots ,y_{k-1})$的分布知道了，可以得到$P(x_k,y_k|y_1,y_2,\dots ,y_{k-1})$的分布，该分布仍然是多元正态分布，分布为
$$P(x_k,y_k|y_1,y_2,\dots ,y_{k-1})\sim N_{n+p}(\left[\begin{array}{c}A{\hat{\mu }}_{k-1}+B{u}_{k-1}\\ H(A{\hat{u}}_{k-1}+B{u}_{k-1})\end{array}\right],\left[\begin{array}{cc}A{\hat{\Sigma }}_{k-1}{A}^T+Q& (A{\hat{\Sigma }}_{k-1}{A}^T+Q)H^T\\ H(A{\hat{\Sigma }}_{k-1}{A}^T+Q{)}^T& H(A{\hat{\Sigma }}_{k-1}{A}^T+Q)H^T+R\end{array}\right])$$

知道上面$P(x_k,y_k|y_1,y_2,\dots ,y_{k-1})$这个概率分布函数后，如何求$P(x_k|y_1,y_2,\dots ,y_k)$,下面给定引理：
$${\left(\begin{array}{c}u\\ v\end{array}\right)}_{n+m}\sim N_{n+m}(\left[\begin{array}{c}{\mu }_u\\ {\mu }_v\end{array}\right],\left[\begin{array}{cc}{\Sigma }_u& {\Sigma }_{uv}\\ {\Sigma }_{vu}& {\Sigma }_v\end{array}\right])$$
$$P(u|v)\sim N_n({\mu }_u+{\Sigma }_{uv}{\Sigma }_v^{-1}(v-{\mu }_v),{\Sigma }_u-{\Sigma }_{uv}{\Sigma }_v^{-1}{\Sigma }_{uv}^T)$$

对于$P(x_k,y_k|y_1,y_2,\dots ,y_{k-1})$，根据以上引理，可以得到
$$P(x_k|y_1,y_2,\dots ,y_k)\sim (A{\hat{\mu }}_{k-1}+B{u}_{k-1}+(A{\hat{\Sigma }}_{k-1}{A}^T+Q)H^T[H(A{\hat{\Sigma }}_{k-1}{A}^T+Q)H^T+R{]}^{-1}[y_k-H(A{\hat{\mu }}_{k-1}+B{u}_{k-1})],(A{\hat{\Sigma }}_{k-1}{A}^T+Q)-(A{\hat{\Sigma }}_{k-1}{A}^T+Q)H^T[H(A{\hat{\Sigma }}_{k-1}{A}^T+Q)H^T+R{]}^{-1}H(A{\hat{\Sigma }}_{k-1}{A}^T+Q{)}^T)$$

上式看起来有点繁琐，我们令${\hat{x}}_{\overline{k}}=A{\hat{\mu }}_{k-1}+B{u}_{k-1}$，$P_{\overline{k}}=A{\hat{\Sigma }}_{k-1}{A}^T+Q$，$K_k=P_{\overline{k}}{H}^T[H{P}_{\overline{k}}{H}^T+R{]}^{-1}$,则$P(x_k|y_1,y_2,\dots ,y_k)$可以被重写成

$$P(x_k|y_1,y_2,\dots ,y_k)\sim ({\hat{x}}_{\overline{k}}+K_k(y_k-H{\hat{x}}_{\overline{k}}),P_{\overline{k}}-K_{k}H{P}_{\overline{k}})$$

此时，我们知道$P(x_k|y_1,y_2,\dots ,y_k)\sim ({\hat{x}}_{\overline{k}}+K_k(y_k-H{\hat{x}}_{\overline{k}}),P_{\overline{k}}-K_{k}H{P}_{\overline{k}})$，为了形式上和$P(x_{k-1}|y_1,y_2,\dots ,y_{k-1})\sim N_n({\hat{\mu }}_{k-1},{\hat{\Sigma }}_{k-1})$一致，我们记
$${\hat{\mu }}_k={\hat{x}}_{\overline{k}}+K_k(y_k-H{\hat{x}}_{\overline{k}})$$

$${\hat{\Sigma }}_k=P_{\overline{k}}-K_{k}H{P}_{\overline{k}}=(I-K_{k}H)P_{\overline{k}}$$

那么有$P(x_k|y_1,y_2,\dots ,y_k)\sim N_n({\hat{\mu }}_k,{\hat{\Sigma }}_k)$，所以在当前时间$t=k$时，在发生了测量值$y_1,y_2,\dots ,y_k$的情况下，系统真实状态$x_k$为${\hat{\mu }}_k$的概率最大，我们也说${\hat{\mu }}_k$是系统在$t=k$时真实状态$x_k$的最优估计。

总结一下上面的推导，一共五个式子。首先，我们知道$t=k-1$时系统的状态$x_{k-1}$符合$P(x_{k-1}|y_1,y_2,\dots ,y_{k-1})\sim N_n({\hat{\mu }}_{k-1},{\hat{\Sigma }}_{k-1})$，即系统在$t=k-1$时的真实状态$x_{k-1}$的最优估计是${\hat{\mu }}_{k-1}$。现在根据$P(x_{k-1}|y_1,y_2,\dots ,y_{k-1})\sim N_n({\hat{\mu }}_{k-1},{\hat{\Sigma }}_{k-1})$可以推算出$t=k$时系统的状态$x_k$符合$P(x_{k-1}|y_1,y_2,\dots ,y_k)\sim N_n({\hat{\mu }}_k,{\hat{\Sigma }}_k)$，
计算公式为
$${\hat{x}}_{\overline{k}}=A{\hat{\mu }}_{k-1}+B{u}_{k-1}$$

$$P_{\overline{k}}=A{\hat{\Sigma }}_{k-1}{A}^T+Q$$

$$K_k=P_{\overline{k}}{H}^T[H{P}_{\overline{k}}{H}^T+R{]}^{-1}$$

$${\hat{\mu }}_k={\hat{x}}_{\overline{k}}+K_k(y_k-H{\hat{x}}_{\overline{k}})$$

$${\hat{\Sigma }}_k=P_{\overline{k}}-K_{k}H{P}_{\overline{k}}=(I-K_{k}H)P_{\overline{k}}$$

谈点对卡尔曼滤波器的理解，卡尔曼滤波器的实际做的就是时刻$t=k-1$，在系统观测量$y_1,y_2,\dots ,y_{k-1}$已知的情况下，根据系统状态$x_{k-1}$的条件概率密度函数，来计算在$t=k$时，且系统观测量$y_1,y_2,\dots ,y_k$已知的情况下，系统状态$x_k$的条件概率密度函数。如下图所示，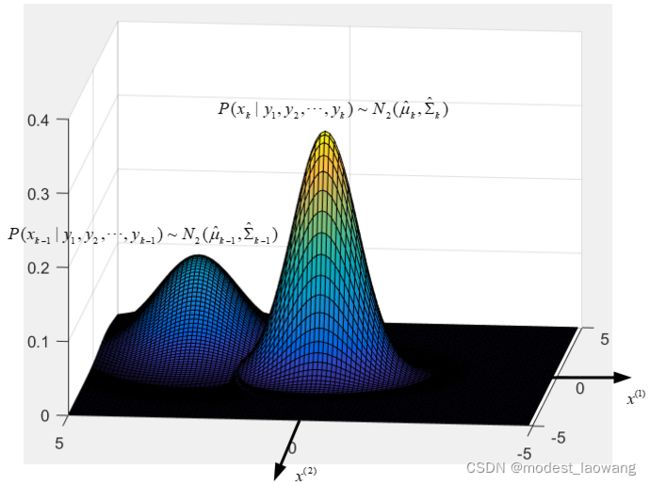
图中的系统状态为$x$，$x:2\times 1$，即系统状态有两个分量$x^{(1)}$和$x^{(2)}$，系统的条件密度函数由服从$N_2({\hat{\mu }}_{k-1},{\hat{\Sigma }}_{k-1})$的多元高斯分布变成了另一个服从$N_2({\hat{\mu }}_k,{\hat{\Sigma }}_k)$的多元高斯分布。

卡尔曼滤波器的相关基础知识

笔者是自动化专业的，关于卡尔曼滤波器中的状态方程和观测方程，我就没多说，默认读者都是会的，如果大家不是很清楚，推荐阅读刘豹的《现代控制理论》第一章。

关于卡尔曼滤波器最难的也就是概率推算，这一块基本上是多元正态分布的知识，仅仅学习过概率论的同学应该看着很费解，推荐阅读高惠璇的《应用多元统计分析》第二章，从中可以系统的了解多元正态分布的定义和相关性质，本文的推导使用的知识都能从中找到对应的推导和证明。

关于和卡尔曼滤波器的相关知识很接近的知识是HMM（Hidden Markov Model）和粒子滤波，推荐看B站的徐亦达老师的卡尔曼滤波器部分，HMM和粒子滤波部分，讲的真的很好（建立在读者有扎实的数学基础层面上）
B站徐亦达老师卡尔曼滤波器讲解视频

卡尔曼滤波器的仿真

下面放上MATLAB仿真程序，

%%% kalman filter %%%
% the state space function is as follows
% x_{
     k} = Ax_{
     k-1}+Bu_{
     k-1}+ w_{
     k-1}
% where Cov(ww^{
     T}) = Q . Matrix size: A: n×n  B: n×p  
% the measurement function is as follows
% z_{
     k} = Hx_{
     k} + v_{
     k}
% where Cov(vv^{
     T}) = R . Matrix size: H: m×n

% k=1:   P(x_{
     1}|y_{
     1})=N(posterior probability{
     u_{
     1}},posterior probability{
     sigma_{
     1}})
% k=2:   P(x_{
     2}|y_{
     1})=N(prior probability{
     u_{
     2}},prior probability{
     sigma_{
     2}}) 
%        P(x_{
     2}|y_{
     1},y_{
     2})=N(posterior probability{
     u_{
     2}},posterior probability{
     sigma_{
     2}})
% k=t:   P(x_{
     k}|y_{
     1},y_{
     2},...,y_{
     k})=N(prior probability{
     u_{
     k}},prior probability{
     sigma_{
     k}}) 
%        P(x_{
     k}|y_{
     1},y_{
     2},...,y_{
     k})=N(posterior probability{
     u_{
     k}},posterior probability{
     sigma_{
     k}})

A = [0, 0.1, 0; 0, 0.2, 0; 0, 0, 0.3];
B = [0.1; 0.1; 0.1];
H = [1, 0, 0;0, 1, 0;0, 0, 1];
Q = [0.01, 0, 0; 0, 0.01, 0; 0, 0, 0.01]; % 注意这里我仿真设置的协方差矩阵中，噪声的每一个分量都是不相关的，实际中不同噪声分量可以相关。
R = [0.09, 0, 0;0, 0.09, 0;0, 0, 0.09]; % 注意这里我仿真设置的协方差矩阵中，噪声的每一个分量都是不相关的，实际中不同噪声分量可以相关。

posterior_probability_u=[0;0;0]; % 时间步为1时的初始化状态期望
posterior_probability_sigma=[0,0,0;0,0,0;0,0,0]; % 初始时刻t=1时,初始化状态协方差矩阵
real_state=zeros(3,1000);
estimate_state=zeros(3,1000);
input_u=ones(1,1000);
measurement_value=zeros(3,1000);
estimate_state(:,1)=posterior_probability_u; 
t=150;
for i = 2:t
    a=normrnd(0,0.1,[3,1]);
    real_state(:,i)=A*real_state(:,i-1)+B*input_u(:,i-1)+a;
    measurement_value(:,i)=H*real_state(:,i)+normrnd(0,0.3,[3,1]);
    prior_probability_u=A*estimate_state(:,i-1)+B*input_u(:,i-1);
    prior_probability_sigma=A*posterior_probability_sigma*A'+Q;
    kalman_gain=prior_probability_sigma*H'/(H*prior_probability_sigma*H'+R);
    estimate_state(:,i)=prior_probability_u+kalman_gain*(measurement_value(:,i)-H*prior_probability_u);
    posterior_probability_sigma=(eye(3,3)-kalman_gain*H)*prior_probability_sigma;
end
figure(1);
plot(real_state(1,1:t),'r');
hold on;
plot(measurement_value(1,1:t),'y');
hold on;
plot(estimate_state(1,1:t),'b');
legend('real state','mesurement value','estimate state');

figure(2);
plot(real_state(2,1:t),'r');
hold on;
plot(measurement_value(2,1:t),'y');
hold on;
plot(estimate_state(2,1:t),'b');
legend('real state','mesurement value','estimate state');

上面程序中的$t=1$时，$P(x_1|y_1)\sim N_3({\hat{\mu }}_1,{\hat{\Sigma }}_1)$中的${\hat{\mu }}_1$对应的是posterior_probability_u，${\hat{\Sigma }}_1$对应的是posterior_probability_sigma，这是我们事前根据自己对系统的了解设置的，在上述程序中的系统的真实初始值$x_1=[0;0;0]$,当我们把posterior_probability_u初始化为$[0;0;0]$时，对于系统状态的第一个分量$x^{(1)}$仿真结果如下图，

上图中的红线是系统的真实状态值（因为我是在仿真，我计算出来了系统真实值，在实际工程中，我们是不知道系统状态的真实值的），黄线是系统中的测量值（可以认为是传感器传回来的数据），蓝线是卡尔曼滤波器估计出来的系统状态最优值。
这个仿真是我根据实际情况可能出现的情况给出的仿真，在使用陀螺仪加速度计这类传感器时，传感器测量噪声比较大，所以黄线波动幅度很大，红线按道理波动可以再小一点，这里我把系统状态方程中的噪声设置的有点大，在不少的控制系统中，由于反馈的作用，系统中的噪声会相对小一些，所以从图中可以看出来，估计出来的状态最优值波动还是较小的，和系统真实状态值比较贴近，传感器的噪声被很大程度抑制了，如果只使用传感器的读数作为系统状态值，那么可以看到两者差距还是很大的。
如果传感器噪声很小，我们完全可以不用卡尔曼滤波器，因为测量值基本就是系统真实状态值了。这很容易理解，为了验证一下，我把程序中的$R$的改为R = [0.0001, 0, 0;0, 0.0001, 0;0, 0, 0.0001],仿真结果如下，红线和黄线基本重合，反而卡尔曼滤波器估计出来的最优值不如测量值靠谱。
再回到系统初始设定的问题，在$t=1$时，系统初始$P(x_1|y_1)\sim N_3({\hat{\mu }}_1,{\hat{\Sigma }}_1)$中的${\hat{\mu }}_1$对应的是posterior_probability_u，在上述程序中的系统的真实初始值$x_1=[0;0;0]$,当我们把posterior_probability_u初始化为$[1;1;1]$时，这个设置和系统真实情况出入很大，对于系统状态的第一个分量$x^{(1)}$仿真结果如下图，

可以看出来即使初始假设和系统真实情况出入比较大，关于系统状态的最优估计还是很快回归到系统真实状态值附近，这是因为有测量值帮助修正最优估计。所以允许在初始假设时，出现与系统真实状态分布的偏差。

卡尔曼滤波器的总结

卡尔曼滤波器利用了两条线，第一条线是系统的状态方程，状态方程保证了系统状态变量的一个基本物理变换过程，即使有系统噪声的存在，也可以根据系统的时刻$t=k-1$的状态值得到$t=k$时，系统状态值大概值（概率分布）。第二条线是我们有系统的传感器传回来的测量值（大多时候传感器的测量噪声比较大）。根据这两条线，来计算系统最可能的状态值（即最优估计${\hat{\mu }}_k$）。