(4)一文懂“CNN模型” 参数量与计算量
1、基础知识
1)计算量主要体现了芯片的运算能力即算力,参数量取决于显存大小。
2)计算量主要在于卷积(或Dot),参数量主要在于全连接层。
1.1 模型说明
首先明确模型的计算量一般是衡量冻结模型(.pd)的,.ckpt在权重和偏置按照高斯分布初始化时一般计算量要大于冻结模型,所以我们要首生成模型的冻结文件(.pd)。
1.2 度衡量标准
FLOPS:注意全大写,是floating point operations per second的缩写,意指每秒浮点运算次数,理解为计算速度。是一个衡量硬件性能的指标。
FLOPs:注意s小写,是floating point operations的缩写(s表复数),意指浮点运算数,理解为计算量。可以用来衡量算法/模型的复杂度。
MACCs:是multiply-accumulate operations,也叫MAdds,意指乘-加操作(点积运算),先乘起来再加起来的运算次数。理解为计算量,也叫MAdds, 大约是 FLOPs 的一半。
1.3 芯片峰值算力
以燧原科技“云燧T10”人工智能训练芯片为例,主频1.15GHZ,32个SIP,单个sip一个指令周期可以计算256个MAC(乘法和加法分开统计,就是512个浮点运算),故FP32峰值算力为:
1.15G * 32 * (256*2) = 18.4TFOLPS = 9.2 TMACCs
2、各种计算对于FLOPs的消耗
2.1 卷积层(convolutional layer)
卷积层的乘-加操作次数很多,占总体的大头。卷积层要单独算而不是用全连接层的结论,是因为输入至少是三维的:H×W×C。对于这样的卷积层,MACCs 有:K×K×Cin×Hout×Wout×Cout
每个output_featuremap即Cout对应的(Hout*Wout)点都是一次(k*k)在input_featuremap上的一次Conv的乘积累加运算,即滤波器(k*k)和input_H*W的对应元素相乘,然后再求和。每次移动都是一次MACCs。同样,这里也忽略了偏置和激活函数。不应该忽略的是 stride(步长)、dilation factors(漏孔/膨胀卷积)、padding(填充),这就是为什么直接从输出尺寸 Hout×Wout 开始算的原因都已经考虑在内了。
2.2 全连接层(fully connection layer)
权重 W 是一个 I×J 矩阵,输入 x 是 I 维实值向量,b 是 J 维偏置。输出 y 也是 J维实值向量。FC 层的 MACCs 也不难计算。FC 是向量与矩阵的点积,每一组点积发生在输入 x同权重 W 某一列之间,计有 I MACCs,一共要计算 J 组点积,所以 FC 层的 MACCs 总计 I×J,跟权重的尺寸一致。偏置项 b对 MACCs 的影响可以忽略不计。而上面也提到 MACCs 中加法比乘法少一次, b刚好补上了这个缺。
所以,对 I的输入、权重为 I×J 的权重矩阵和 J 的输出,MACCs 为 I×J ,FLOPs 为 (2I−1)×J 。
2.3 batch normalization
z = gamma * (y - mean) / sqrt(variance + epsilon) + beta
每个通道上都存在一组 mean 、beta 、gamma 、variance ,C个通道就有 C×4个可学习的参数。而且 BN 是作用在每一个元素上的,这样看来,造成的 FLOPs 应该不少。在 BN 直接连接卷积层的情况下,即 Conv-BN-ReLU 时,通过一组推导,可以将 BN 的计算整合到卷积层当中(注意这是 inference 的情况,跟训练阶段差别很大),从而消去的 BN 层造成的 FLOPs。如果是 Conv-ReLU-BN 的结构这一套就行不通了。( BN 层的计算结合到 Conv 层中去,BN 层的 FLOPs 消失了,Conv 层需要乘一个常系数)。即从结果上来说,在 inference 时模型中的 BN 层实际被消去了。
2.4 激活函数
FC 完了接下来通常有个激活函数,ReLU 或者 Sigmoid。激活函数的计算没有点积,所以只用 FLOPS 衡量。对输出为 J的 FC 层,ReLU 有 J FLOPS:
y = max(x, 0)
相比之下 Sigmoid 就复杂很多。
y = 1/(1+exp(-x))
我们把加减乘除、指数、平方根等等运算都算作一次 FLOPs,这里有除法、加法、指数和减法四种运算,所以 FLOPs 就是 J×4。
2.5 其它层
像 Pooling 层虽然确实很关键(Pooling层无参数),但没有用到点积运算,所以 MACCs 不能很好地衡量这部分计算消耗。如果用 FLOPs,可以取 feature map 的尺寸然后乘一个常系数。如 maxpooling 层,stride=2、filter_sz=2(即输出保持相同尺寸),112 x 112 x 128 的feature map,FLOPs就是 112 x 112 x 128 = 1,605,632 。相对卷积层和全连接层的运算,这个计算量比较小,所以也可以忽略不计
3、内存占用
内存带宽其实比 MACCs 更重要。目前的计算机结构下,单次内存访问比单次运算慢得多的多。
对每一层网络,设备需要:
1)从主内存中读取输入向量 / feature map
2)从主内存中读取权重并计算点积
3)将输出向量或 feature map 写回主内存
涉及大量的内存访问。内存是很慢的,所以网络层的内存读写对速度有很大的影响,可能比计算耗时还要多。
3.1 参数量
全连接层:有 I x J 大小的权重矩阵,加上偏置向量共计 (I + 1) x J 。
卷积层: kernel 通常是正方形的,对 kernel_sz = K 和输入通道为 Cin 、输出 Cout 和额外的 Cout 个偏置的情况,共有 (K x K x Cin + 1) x Cout 个参数。对比之下卷积层的参数量远小于全连接。
池化层:无参数
举例说明:
全连接层:有4096个输入和4096个输出,所以权重数 (4096+1) x 4096 = 16.8M 。
卷积层:3 x 3 、48个卷积核,在64x64 、32个通道的输入上计算,共有 权重数3 x 3 x 32 x 48 + 48 = 13.5k 。
注意:卷积层的输入实际是全连接层的32倍(通道),输出是48倍,然而权重数只有后者的千分之一不到。
3.2 feature maps和中间结果
举例说明:卷积层的input是 224x224x3=150,528 ,把所有这些值读出来需要访问 150,528 次内存。如果卷积核是 KxKxCout ,还要乘上这个系数(因为每次卷积都要访问一遍)。output拿 stride=2, kernel 数为32的情况来说,输出的 feature map 尺寸为 112x112x32=401,408次内存访问。
# 所以,每层的内存访问总数如下:
input = (Hin x Win x Cin) x (K x K) x Cout
output = Hout x Wout x Cout
weights = K x K x Cin x Cout + Cout
即:
input = (224 x 224 x 3) x (3 x 3) x 32 = 43,352,064
output = 112 x 112 x 32 = 401,408
weights = 3 x 3 x 3 x 32 + 32 = 896
total = 43,754,368 = 41.7MB
# 当网络层数加深时,Hin Win 会越来越小,但通道数会变得很大:
input = 28 x 28 x 256 x 3 x 3 x 512 = 924,844,032
output = 28 x 28 x 512 = 401,408
weights = 3 x 3 x 256 x 512 + 512 = 1,180,160
total = 926,425,600 = 883.5MB
# 这种情况下 weights 部分也会变得很大,所以是不能忽略的。
4、以Lenet5为例
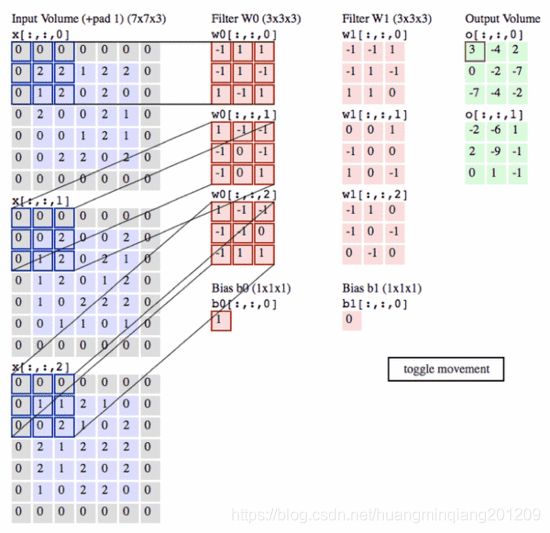
一个卷积神经网络的基本构成一般有卷积层(convolutional layer)、池化层(pooling layer)、全连接层(fully connection layer)。以caffe中的LeNet-5为例,分析卷积层和全连接层的参数数量和计算量情况。卷积层的基本原理就是图像的二维卷积,以步长stride进行滑动,滑动一次则进行一次模板内的对应相乘求和作为卷积后的值。在CNN的卷积层中,首先是卷积层维度提升到三维、四维,与二维图分别进行卷积,然后合并。具体如下图所示:
该图中左边的一幅3个通道的输入图,中间是卷积层,尺寸为3*(3*3)*2,这里就是三维卷积,得到的特征图还是一个通道,有2个三维卷积得到2个featuremap。
4.1 卷积层
name: "LeNet"
layer {
name: "data"
type: "Input"
top: "data"
input_param { shape: { dim: 64 dim: 1 dim: 28 dim: 28 } }
} # 输入是28×28的灰度图,batchsize是64
layer {
name: "conv1"
type: "Convolution"
bottom: "data"
top: "conv1"
param {
lr_mult: 1
}
param {
lr_mult: 2
}
convolution_param {
num_output: 20
kernel_size: 5
stride: 1
weight_filler {
type: "xavier"
} # 卷积核为5×5,output feature 20个
bias_filler {
type: "constant"
}
}
}
layer {
name: "pool1"
type: "Pooling"
bottom: "conv1"
top: "pool1"
pooling_param {
pool: MAX
kernel_size: 2
stride: 2
}
}下面我们来看一下日志文件:
db_lmdb.cpp:40] Opened lmdb ./mnist_train_lmdb
data_layer.cpp:41] output data size: 64,1,28,28
net.cpp:150] Setting up mnist
net.cpp:157] Top shape: 64 1 28 28 (50176) # (50176*4=200704=196KB)
net.cpp:157] Top shape: 64 (64)
net.cpp:165] Memory required for data: 200960=196.25KB
layer_factory.hpp:77] Creating layer conv1
net.cpp:100] Creating Layer conv1
net.cpp:444] conv1 <- data
net.cpp:418] conv1 -> conv1
common.cpp:36] System entropy source not available, using fallback algorithm to generate seed instead.
net.cpp:150] Setting up conv1
net.cpp:157] Top shape: 64 20 24 24 (737280) #(737280*4=2949120=2.81MB)
net.cpp:165] Memory required for data: 3150080=3MB
layer_factory.hpp:77] Creating layer pool1
net.cpp:100] Creating Layer pool1
13112 net.cpp:444] pool1 <- conv1
net.cpp:418] pool1 -> pool1
net.cpp:150] Setting up pool1
net.cpp:157] Top shape: 64 20 12 12 (184320) #(184320*4=737280=720KB)
net.cpp:165] Memory required for data: 3887360=3.7MB
4.2 全连接层
layer {
name: "ip1"
type: "InnerProduct"
bottom: "pool2"
top: "ip1"
param {
lr_mult: 1
}
param {
lr_mult: 2
}
inner_product_param {
num_output: 500
weight_filler {
type: "xavier"
}
bias_filler {
type: "constant"
}
} # 第一个全连接层的输出元素个数500
}下面我们来看一下日志文件:
net.cpp:157] Top shape: 64 50 4 4 (51200)
net.cpp:165] Memory required for data: 4911360 = 4.68MB
layer_factory.hpp:77] Creating layer ip1
net.cpp:100] Creating Layer ip1
net.cpp:444] ip1 <- pool2
net.cpp:418] ip1 -> ip1
net.cpp:150] Setting up ip1
net.cpp:157] Top shape: 64 500 (32000)
net.cpp:165] Memory required for data: 5039360
layer_factory.hpp:77] Creating layer relu1
net.cpp:100] Creating Layer relu1
net.cpp:444] relu1 <- ip1
net.cpp:405] relu1 -> ip1 (in-place)
net.cpp:150] Setting up relu1
net.cpp:157] Top shape: 64 500 (32000)
net.cpp:165] Memory required for data: 5167360
卷积部分得到的featuremap为4×4×50,全连接部分是将featuremap展开成一维向量再与全连接相连。所以单样本(batchsize=1)前向传播计算量为:(4×4×50)×500 = 400 000,参数数量为 (4×4×50)×500 = 400 000。在全连接中计算量和参数比始终为1,就是源于全连接的特性。
4.3 分析对比
conv-1的计算量/参数比为576,ip1的计算量/参数比为1。
conv-1的计算量是ip1的0.72,而参数是0.00125。
也就是说卷积层主要是大大减少了连接参数,所以在CNN网络中一般卷积层参数量占比小,计算量占比大,而全连接中参数量占比大,计算量占比小。大致卷积层的计算量是全连接的20%。所以我们需要减少网络参数、权值裁剪时主要针对全连接层;进行计算优化时,重点放在卷积层。卷积层的优化方法:
1. Low rank(低秩):(单层到多层)SVD分解fc层和卷积核,tensor展开。
2. Pruning(剪枝):去掉某些神经元连接训练找到重要的连接。
3. Quantization(量化)权值量化,霍夫曼编码,codebook编码,hashed-net,PQ-CNN。
4. Fixed-point/binary net,BNN。
5、经典模型
| AlexNet |
VGG16 |
Inception-V3 |
|
| 模型内存(MB) |
>200 |
>500 |
90~100 |
| 模型参数(百万) |
60 |
138 |
23.2 |
| 模型计算量(百万) |
720 |
15300 |
5000 |
以alexnet为例:参数量:6000万,每个参数都是float,也就是一个参数是4字节,总的字节数是24000万字节 = 24000万/1024/1024 = 228mb
1)为什么模型之间参数量差距这么大
全连接层对参数量影响最大,alex,vgg有很多fc(全连接层),Inceptionv3就一个fc
2)计算量
Inceptionv3其实这个模型不大,也就是参数量不大,因为就1个fc。但是他的计算量较大,关键在于输入与卷积操作
参考:https://cloud.tencent.com/developer/article/1422751