Pytorch学习笔记(一)搭建一个CNN神经网络
本文根据pytorch官方教程编写,如果有兴趣的人可以直接去查看pytorch的官方文档。
那么现在就直接开始吧!
第一步就是直接导入包
import torch.nn as nn
import torch.nn.functional as F
import torch
然后嘛!就是通过继承nn.Module来编写模型类。
class Net(nn.Module):
def __init__(self):
super(Net,self).__init__()#继承nn.Module中的代码
self.conv1=nn.Conv2d(1,6,5)#输入通道数为1,输出通道数为6,卷积核大小为(5,5),步长默认为1
self.conv2=nn.Conv2d(6,16,5)
self.Pool=nn.MaxPool2d(2,2)#最大池化层 2*2
#开始构建线性层
self.fc1=nn.Linear(16*5*5,120)#输入层大小为400,隐含层大小为120
self.fc2=nn.Linear(120,84)#隐含层1大小为120,隐含层2大小为84
self.fc3=nn.Linear(84,10)#隐含层2大小为84,输出层大小为10
def forward(self,x):
x=self.Pool(F.relu(self.conv1(x)))#进行池化操作,F.relu()是激活函数
x=self.Pool(F.relu(self.conv2(x)))
x=x.view(-1,self.num_flat_features(x))#通过view函数将张量x变成 16*5*5的一维向量
x=F.relu(self.fc1(x))#在第一个全连接层经过激活函数relu,之后在传到后面去
x=F.relu(self.fc2(x))
x=self.fc3(x)#最后一层,因此不用激活函数激活了
return x
def num_flat_features(self,x):
size=x.size()[1:]#获取第一层全连接层的大小,输出为torch.Size([16, 5, 5])
num_features=1
for s in size:
num_features*=s
return num_features
现在开始精彩一些的地方吧!
比如输出一下我们的模型,看看他的内部机构
net=Net()#实例化一个模型
print(net)
如果你的代码没有写错的话,你就会得到下面的这些输出。
如果你能结合我们上面的代码观看的话,你就会发现,这些东西就是我们所定义的卷积层,池化层以及全连接层。
Net(
(conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
(conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(Pool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(fc1): Linear(in_features=400, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=84, bias=True)
(fc3): Linear(in_features=84, out_features=10, bias=True)
)
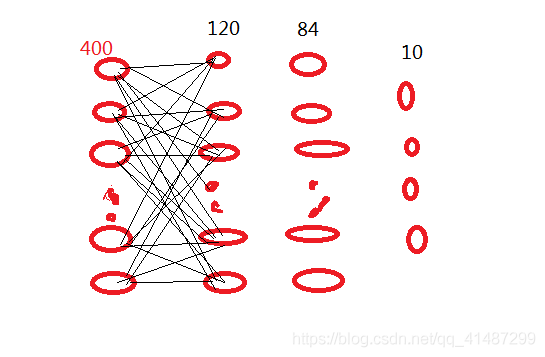
大致形状就是这样了,后面的这些线我就不连了,懒得连。还有就是别忘了他们还有卷积层和池化层。
如果我们来观察一下模型的参数吧!
params=list(net.parameters())#所谓参数就是对这些卷积层,全连接层的一个缩写。如params[0]就是conv1 (6,1,5,5),params[1]就是conv1的输出量为6
print(len(params))
print(params[0].size())#建议把这从0-9几个参数都看一下,也许你会对这种模型的构建有一个更加清晰的认知
输出如下:
10
torch.Size([6, 1, 5, 5])
再来,我们来看这个编写出来的模型,会有什么样的输出呢!
input =torch.randn(1,1,32,32)#随机创建一个输入张量
out=net(input)#先试试将其放入模型得到的结果
print(out)
输出如下:
tensor([[ 0.0013, -0.0339, -0.0306, 0.0887, -0.0689, -0.0216, -0.0481, -0.0103,
-0.0592, -0.0732]], grad_fn=)
由此我们可以看到,他的输出结果正好就是(1,10)的张量,也就是我们的最后一层全连接层的输出。因为最后的这一层是一共只有十个神经元,所以输出时自然会是10个输出。
如果你的项目是做的01标签输出的话,记得直接把输出层设置成2个神经元哟!
接着我们开始反向传播,并计算其损失值吧!
net.zero_grad()#神经网络中的梯度缓冲区全部清零,否则就会与已经有的梯度混到一起
out.backward(torch.randn(1,10))#开始使用随机梯度开始反向传播,反向传播前conv1的偏置项为空或者说全零
output=net(input)#再次获取其输出
target=torch.randn(10)#确定一个目标值,size要为(1,10)
target=target.view(1,-1)
criterion=nn.MSELoss()#定义损失函数
loss=criterion(output,target)#通过输出结果与目标值来计算损失函数,或者说是实际网络输出值与预期值之前的差距
print(loss)
输出结果如下:
tensor(0.6017, grad_fn=)
看到他的grad_fn属性了吗?
他们的grad_fn属性已经变成了我们定义的MSELoss()了。
上面的代码是不合格的。它只是给了一个目标,然后就直接计算其损失值。
我们的模型都是需要训练的,因此它应该拥有一个优化迭代器。
对此,torch给了我们一个包 optim。
我们经过会用梯度下降的方法来进行迭代优化:
其公式如下:
weight = weight - learning_rate * gradient
当然,这并不是我们这里要使用的优化算法。
写出这个只是为了让你稍微对这个优化算法,有一些简单的认知,就是我们学习线性神经网络时候的梯度下降算法,只是这里改成了其他更加优秀的算法罢了。
我们现在使用这个包来定义一个随机梯度下降算法的优化器吧!
SGD(Stochastic gradient descent)
import torch.optim as optim
optimizer=optim.SGD(net.parameters(),lr=0.01)#定义SGD优化器,传入模型参数和学习率
optimizer.zero_grad()
output=net(input)
loss=criterion(output,target)
loss.backward()#根据误差进行反向传播
optimizer.step()
print(loss)
输出如下:
tensor(0.6186, grad_fn=)
我们这样当然是看不出什么东西的,但是我们能够看到这个loss的值,进行了一些改变,当然我们的学习率定得太小了。所以并不太明显。