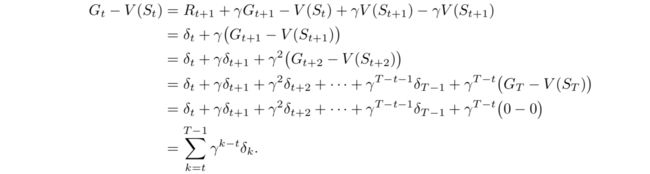概述
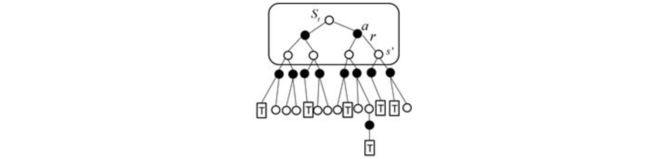
时序差分算法是一种无模型的强化学习算法。它继承了动态规划(Dynamic Programming)和蒙特卡罗方法(Monte Carlo Methods)的优点,从而对状态值(state value)和策略(optimal policy)进行预测。从本质上来说,时序差分算法和动态规划一样,是一种bootstrapping的算法。同时,也和蒙特卡罗方法一样,是一种无模型的强化学习算法,其原理也是基于了试验。虽然,时序差分算法拥有动态规划和蒙特卡罗方法的一部分特点,但它们也有不同之处。以下是它们各自的backup图:
根据它们的backup图可以知道,动态规划的backup操作是基于当前状态和下一个状态的reward,蒙特卡罗方法的backup是基于一个完整的episode的reward,而时序差分算法的backup是基于当前状态和下一个状态的reward。其中,最基础的时序差分算法被称为TD(0)。它也有许多拓展,如n-step TD算法和TD(lambda)算法。
Stationary Environment和Nonstationary Environment的区别
Stationary Environment即为固定的环境,也就是说采取相同的动作时,状态和环境是固定不变的。如:垃圾回收机器人每次充完电之后电都是满的。而Nonstationary Environment与此相反,在采取相同的动作时,状态和环境是不确定的。如:转一下抽奖转盘,它每次停止的位置都是不一样的。
TD(0)时序差分算法
时序差分算法和蒙特卡罗方法一样,仍然有两部分计算。第一部分是时序差分的预测(即计算state value),第二部分是时序差分的控制(TD control),其目的是为了得到最优的策略(optimal policy)。
时序差分预测(TD Prediction)
预测是为了计算状态值(state value)。在计算的时间上,时序差分比蒙特卡罗方法更快一些。其计算公式分别如下所示:
根据公式,TD只需要等到跳转到下一个状态时,便可得知当前状态的state value。但是,蒙特卡罗方法则需要等到整个试验结束之后才可以得到当前状态的state value值。因为,时序差分算法计算value值时,是根据当前状态和接下来的状态来计算,因此是有偏差的,但方差很小。相反,蒙特卡罗方法是无偏差的,但是方差却很大。
时序差分和蒙特卡罗方法的学习都是通过试验采样来计算value值的,采样致使我们无法得到完整的在当前状态跳到下一个状态的分布。可以清晰的从上面的backup 图了解到,只有DP是基于所有的下一个状态的分布。
TD算法和MC算法更新的那一部分被我们成为error(即真实value和评估的value的差值),如下所示:
因为是更新过程,所以其目的就是为了使最终预测的value值与真实的value值的误差尽量小,也就是使其error最小化。在预测的计算公式中,alpa代表的是步长,类似于梯度下降里面的步长。为什么不让error直接变到最小(为零)呢?其原因和我们平常所学的Gradient Descent概念是一样的。因为,我们使用的是抽样的方法,并没有得到真正的数据分布,而如果步长很大的话反倒会使计算value的收敛速度下降。其TD Prediction的伪代码如下:
Batch TD(0)
在对state value进行预测时,我们不仅可以一个试验一个试验的更新,同时,也可以一批一批的进行更新。这就是我们所说的batch TD(0)。
例1: 假如我们对一个随机游走(Random Walk)的游戏进行state value的预测。我们通过一批(8个)试验得到了状态和相应的reward,如下所示:
A:0, B:0 B:1 B:1 B:1 B:1 B:1 B:0 B:1
我们很容易计算出B的value值应该为四分之三。因为在这8个试验中,B为1的总共有六个。而A的value值是多少呢?可能有人会说是0,因为只有一次试验,而且A的reward还为零。但其实答案也是四分之三。要知道TD计算A的value值会根据下一个状态的reward计算的,因为只有一个A试验,且状态被转换到了B状态。因此,TD会推断从A到B的概率应该是100%,所以通过计算,A的value值即为0 + 3 / 4 = 3 / 4。
Sarsa: On-policy TD Control
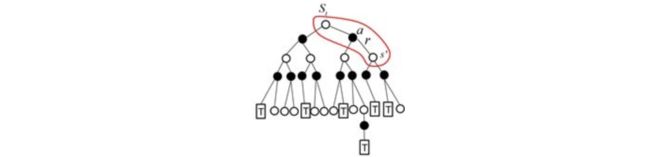
前面在讲蒙特卡罗方法时,我们已经说明了on-policy和off-policy的区别了,这里就不再重复。我们知道一个episode是由多个state-action对所组成的,如图所示:
Sarsa则是State->action->reward->State->action(St, At, Rt+1, St+1, At+1)的简称。所以,其action value的计算公式为:
其伪代码如下所示:
Q-learning: Off-policy Control
Q-learning是一种off-policy的算法,也就是里面有两个policy。其中,behavior policy是用来去尽可能的探索。其伪代码如下所示:
Expected Sarsa
Expected Sarsa和Q-learning很像, 其区别在于Q-learning中behavior policy计算的是最大值,而Expected Sarsa计算的则是期望,如图所示:
其公式如下所示:
Reference
1. Reinforcement Learning An Introduction
2.强化学习入门 第四讲 时间差分法(TD方法) https://zhuanlan.zhihu.com/p/25913410