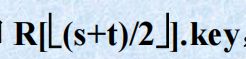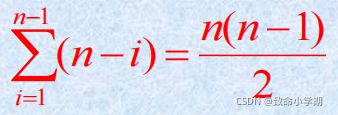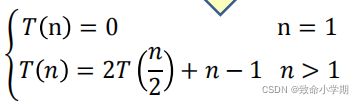【数据结构】第10章 排序
目录
9.1概述
1. 排序方法的稳定和不稳定
2. 内部排序和外部排序
3. 存储结构
4.效率分析
9.2 插入排序
9.2.1 直接插入排序
2. 插入排序的思想
3. 算法概述
4. 直接插入排序算法
5. 算法分析
9.2.2 其它插入排序
折半插入排序
9.2.3 希尔排序
4. 希尔排序算法
9.3 快速排序 ——交换排序类
9.3.1、起泡排序
9.3.2、快速排序
9.4 选择排序
9.4.1 简单选择排序
9.4.1 堆排序
9.5 归并排序
9.6 基数排序
9.7 内部排序方法的比较
9.1概述
1. 排序方法的稳定和不稳定
在排序前后，含相等关键字的记录的相对位置保持不变，称这种排序方法是稳定的；
反之，含相等关键字的记录的相对位置有可能改变，则称这种排序方法是不稳定的。
2. 内部排序和外部排序
在排序过程中，只使用计算机的内存存放待排序记录，称这种排序为内部排序。
排序期间文件的全部记录不能同时存放在计算机的内存中，要借助计算机的外存才能完成排序，称之为“外部排序”。
内外存之间的数据交换次数是影响外部排序速度的主要因素。
3. 存储结构
#define maxsize 1000//待排顺序表的最大长度
typedef int keytype;//关键字类型为int类型
typedef struct
{
keytype key;//关键字项
infotype otherinfo;// 其他数据项
}RcdType; //记录类型
typedef struct
{
RcdType r[maxsize+1];//r[0]闲置
int length;//长度
}SqList; //顺序表类型4.效率分析
(1) 时间复杂度：
关键字的比较次数和记录移动次数
(2) 空间复杂度：
执行算法所需的附加存储空间
(3) 稳定算法和不稳定算法。
9.2 插入排序
9.2.1 直接插入排序
直接插入排序从什么位置开始？
从第二个元素开始。一共进行n-1次。
0号单元不存，哨兵。
直接插入排序第i趟后序列有什么特征？
前i+1个记录是有序的。
2. 插入排序的思想
(1)一个记录是有序的；
(2)从第二个记录开始，按关键字的大小将每个记录插入到已排好序的序列中；
(3)一直进行到第n个记录。
3. 算法概述
(1)将序列中的第1个记录看成是一个有序的子序列;
(2)从第2个记录起按关键字大小逐个进行插入，直至整个序列变成按关键字有序序列为止；
整个排序过程需要进行比较、后移记录、插入适当位置。从第二个记录到第n个记录共需n-1趟。
4. 直接插入排序算法
#define maxsize 1000//待排顺序表的最大长度
typedef int keytype;//关键字类型为int类型
typedef struct
{
keytype key;//关键字项
infotype otherinfo;// 其他数据项
}RcdType; //记录类型
typedef struct
{
RcdType r[maxsize+1];//r[0]闲置
int length;//长度
}SqList; //顺序表类型
//直接插入排序
void InsertionSort(SqList &L)
{
int i,j;
for(i=2;i<=L.length ;i++)
{
if(L.r[i].key 5. 算法分析
(1)稳定性
9.2.2 其它插入排序
折半插入排序
, 移动 O(n 2 );
//折半插入排序
void BiInsertionSort(SqList &L)
{
int i,j;
for(i=2;i<=L.length,i++)//从第2到n个元素
{
if(L.r[i].key < L.r[i-1].key )//比较 如果比后面值小 存到哨兵
{
L.r[0]=L.r[i];
}
// 1..i-1中折半查找位置
low=1;
high=i-1;
while(low<=high)
{
mid=(low+high) /2;
if(L.r[0].key < L.r[mid].key )
{
high=mid-1;
}
else
{
low=mid+1;
}
}
//找到插入位置high
for(j=i-1;j>=high+1;--j)
{
L.r[j+1]=L.r[j];//后移
}
L.r[j+1]=L.r[0];//插入
}
} 9.2.3 希尔排序
4. 希尔排序算法
void ShellInsert(SqList &L,int dk)
{
int i,j;
//从dk+1开始
for(i=dk+1 ; i<=L.length;i++)
{
//从当前下标向前 与同一小组的数据进行比较，如果前面数据大，就把前面数据赋值给当前位置
if( LT(L.r[i].key ,L.r[i-dk].key ) )//同一组元素中前一个相比较
{
L.r[0]=R.r[i];//暂存哨兵
for(j=i-dk; j>0 &&(LT(L.r[0].key,L.r[j].key ) ) ; j-=dk )
{
//后移
L.r[j+dk]=L.r[j];
}
//插入位置
L.r[j+dk]=L.r[0];
}
}
}
void ShellSort(SqList &L,int delta[],int t)
{
//1.获取数组长度
int len=L.length;
//2.获取初始的间隔长度
int dk=length/2;
//
while(dk>=1)
{
ShellInsert(L,dk);
dk=dk/2;
}
}9.3 快速排序 ——交换排序类
9.3.1、起泡排序
起泡排序是稳定的排序方法。
(2)时间是复杂性
最好情况：比较O(n), 移动O(1)
最坏情况：比较O(n2), 移动O(n2)
平均情况：O(n2)
(3)空间复杂性
O(1)
void BubbleSort(SqList &L)
{
int i,j,noswap;
SqList temp;
//int n=L.length;
for(i=1;i<=n-1;i++)
{
noswap=1;
for(j=1;j<=n-i;j++)
{
if(L.r[j].key > L.r[j+1].key )//后面小 交换
{
temp=L.r[j];
L.r[j]=L.r[j+1];
L.r[j+1] =temp;
noswap=0;
}
}
if(noswap==1)break;//如果某趟后序列没有变化，就表示已经排好了。
}
} while
void BubbleSort(Elem R[],int n)
{
i=n;
while(i>1)
{
lastindex=1;
for(j=1;j9.3.2、快速排序
(1)左侧子序列中所有对象的关键字都小于或等于对象v的关键字；
(2)右侧子序列中所有对象的关键字都大于或等于对象v的关键字；
(3)对象v则排在这两个子序列中间(也是它最终的位置)。
int Partition(SqList &L,int low,int high)
{
keytype pivotkey;//基准
L.r[0]=L.r[low];
pivotkey=L.r[low].key;
while(low=pivotkey)
{
--high;
}//找到比基准小的key对应的下标high
L.r[low]=L.r[high];//原本low的位置用这个值代替
while(low 
，进行相互 比较，然后 取 关键字为 “三者之中” 的记录 为枢轴 记
9.4 选择排序
9.4.1 简单选择排序
void SelectSort (Elem R[], int n )
{
// 对记录序列R[1..n]作简单选择排序。
for (i=1; i算法：
void Select(SqList &L)
{
int i,j,min;//min存储L.r[i...n]中最小值的下标
for(i=1;i9.4.1 堆排序
void HeapAdjust(HeapType &H,int s,int m)
{//从H中调整下标s的位置 一共M个元素
int j;
RedType rc;
rc=H.r[s];//将要移动的元素 暂存
//暂存堆顶r[s]到rc
for(j=2*s ; j<=m; j*=2)//2*s是左孩子
{
//如果左孩子<右孩子
if(j=H.r[j].key)//如果基准值大于等于j的key
break;//纵比,如果…，定位成功
H.r[s]=H.r[j];//指向当前结点的左孩子
s=j;//
//否则,r[j]上移到s,s变为j, 然后j*=2,进入下一层
}
H.r[s]=rc;//插入
// 将调整前的堆顶记录rc到位置s中
}
void HeapSort(HeapType &H)
{
int i;
RcdType temp;
for(i=H.length/2 ;i>0;--i)//建堆
{
HeapAdjust(H,i,H.length);
}
for(i=H.length ;i>1;--i)
{
//交换r[1]和r[i]
temp=H.r[i];
H.r[i]=H.r[1];
H.r[1]=temp;
HeapAdjust(H,1,i-1); //调整，使得1~i-1符合堆的定义
}
} 9.5 归并排序
二路归并排序的思想是：将待排序 的数列分成相等的两个子数列(数量 相差±1)，然后，再使用同样的算 法对两个子序列分别进行排序，最 后将两个排好的子序列归并成一个 有序序列。
| 算法设计与描述 MergeSort( A,p,r ) | 算法分析 |
| 输入：n个数的无序序列A[p,r] , 1<= p <= r <= n , | (1)输入n，计算规模是n |
| 输出：n个数的有序序列A[p,r] | |
| MergeSort (A,p,r) { { q <- (p+r)/2 ;//中间 MergeSort (A,p,q); //左侧 MergeSort(A,q+1,r) ;//右侧 Merge (A,p,q,r); } } |
（2）核心操作为 移动盘子 （3） (4)
|
| 算法设计与描述 Merge( A,p,q,r ) | 算法分析 |
| 输入：n按递增顺序排好的 A[p...q] 和 A[q+1...r ] | (1)输入n，计算规模是n |
| 输出:按照递增顺序排序的A[p,r] | |
| Merge (A,p,q,r) { x <- q-p+1 ,y <- r-q;//x,y分别是两个子数组的元素数 A[p...q] -> B[1...x] , A[q+1...r] -> C[1...y] //两个新数组 i <- 1 ,j<- 1 ,k <- p while i<=x and j <= y do { if ( B[i] <= C[ j ] ) //注意是i 和 j { A[k] <- B[i];//较小数 i <- i+1; } else { A[k] <- C[j] ; j <- j+1; } k=k+1; } if(i>x) C[j...y] -> A[k..r] //如果还要剩余的元素，就不需要比较，直接赋值回去就行 else B[i..x] -> A[k...r] } |
（2）核心操作为 移动盘子 （3）根据递推公式，。。。【不全】 |
9.6 基数排序