Python库-numpy详解

numpy 库是 一个科学计算库， 使用方法：import numpy as np

• 用于快速处理任意维度的数组，存储的对象是ndarray
• 用于矩阵运算,存储的对象是matrix

1. ndarray介绍

1. ndarray的属性

item = np.array([[1, 2], [3, 4], [5, 6]])
# ndarray的属性
print('shape 表示数组维度的元组', item.shape)  # (3, 2)
print('ndim 表示数组维数', item.ndim)  # 2
print('size 表示数组中元素个数', item.size)  # 6
print('itemsize 表示一个元素所占字节大小', item.itemsize)  # 4
print('dtype 表示数字元素的类型', item.dtype)  # int32

2. ndarray的形状

ndarray可以是任意维度的数组

# ndarray的形状
a1 = np.array([1, 2])
a2 = np.array([[1, 2], [3, 4]])
a3 = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
print('a1是{0}维数组'.format(a1.ndim))
print('a2是{0}维数组'.format(a2.ndim))
print('a3是{0}维数组'.format(a3.ndim))
# a1是1维数组
# a2是2维数组
# a3是3维数组

3. ndarray的类型

创建ndarray对象时，可以使用dtype参数指定ndarray的类型

# ndarray的类型
item = np.array([[1, 2], [3, 4]], dtype=np.str_)	# 设置类型为字符串
print(item)
#[['1' '2']
# ['3' '4']]

2. ndarray的基本操作

生成数组

1. 生成0和1数组

# 生成一个3行4列的数组，元素为0。注意：默认类型为浮点型 0.
arr_zero = np.zeros([3, 4], dtype=int)
# 生成一个3行4列的数组，元素为1
arr_one = np.ones_like(arr_zero)

2. 从现有数组生成

• array()

a = np.array([[1, 2, 3], [4, 5, 6]])
array = np.array(a)
print(array)

• asarray()

asarray = np.asarray(a)
print(asarray)

• array()和asarray()的区别

a[0, 0] = 100   # 修改元素值
print(array)    # array是深拷贝，修改原数据，现数据不变。相当于复制
print(asarray)  # asarray是浅拷贝，修改原数据，现数据改变。相当于创建快捷方式
# [[1 2 3]
#  [4 5 6]]
# [[100   2   3]
#  [  4   5   6]]

3. 生成固定范围的数组

• linspace(start, stop, num, endpoint) 固定个数，步长相等

# 从0到100，生成11个元素，默认包含stop值100，endpoint=True
arr = np.linspace(0, 100, 11)
print(arr)
# [  0.  10.  20.  30.  40.  50.  60.  70.  80.  90. 100.]

• arange(start, stop, step, dtype) 固定步长

# 从0到50，固定步长10生成int类型元素，不包括stop值
arr2 = np.arange(0, 50, 10, np.int32)
print(arr2)
# [ 0 10 20 30 40]

• logspace(start, stop, num) 生成10的N次幂的数据

# 从10^0开始到10^3结束，生成4个元素
arr3 = np.logspace(0, 3, 4)
print(arr3)
# [   1.   10.  100. 1000.]

4. 生成随机数组 np.random模块

4.1. 均匀分布生成

• rand(d0, d1, … , dn) 返回一个[0.0, 1.0)内的一组均匀分布的数据

a1 = np.random.rand(2, 3)   
print(a1)

• uniform(low, high, size) 从一个均匀分布[low, high)中随机采样，可替代rand()方法 常用

a2 = np.random.uniform(1, 10, (2, 3))
print(a2)

• randint(low, high, size) 从一个均匀分布[low, high)中随机采样,生成N维整数数组

a3 = np.random.randint(1, 10, (2, 3))
print(a3)

生成均匀分布数据的小案例

import matplotlib.pyplot as plt

# 1.准备数据 在[0,1)范围内生成 100000000 个数据
x = np.random.uniform(0, 1, 100000000)
# 2.画布
plt.figure(figsize=(20,8), dpi=100)
# 3.绘制 x为数据， bins是要划分的区间数
plt.hist(x=x, bins=1000)
# 4.显示
plt.show()

数据分布如图所示：

4.2. 正态分布生成

• randn(d0, d1, … , dn) 从标准正态分布中返回一个或多个样本值

a1 = np.random.randn(2, 3)   
print(a1)

• normal(loc, scale, size) loc均值，scale标准差，默认size=None，返回一个值 常用

a2 = np.random.normal(1.75, 1, (2, 3))
print(a2)

• standard_normal(size) 返回指定形状的标准正态分布的数组

a3 = np.random.standard_normal((2, 3))
print(a3)

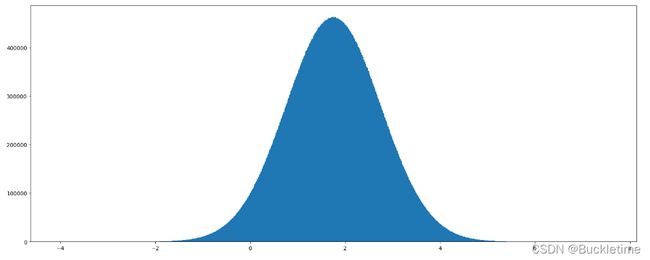
生成正态分布数据的小案例

# 1.准备数据
x = np.random.normal(1.75, 1, 100000000)
# 2.画布
plt.figure(figsize=(20,8), dpi=100)
# 3.绘制 x为数据， bins是要划分的区间数
plt.hist(x=x, bins=1000)
# 4.显示
plt.show()

数据分布如图所示：

数组索引、切片

• 直接索引，先对行索引，再对列索引
• 高维数组索引，从宏观到微观

# 生成一个5行4列的随机数组，范围在40~100
score = np.random.randint(40, 100, (5, 4))
print(score)
# 获取第一行，第三列的值
print(score[0, 2])
# 获取前两行，前三列的值，注意切片是[)，左闭右开
print(score[0:2, 0:3])

修改数组形状

• reshape(shape[,order]) 返回一个新数组，原数组不变，行列顺序不变

# 生成一个4行5列的随机数组，范围在40~100
score = np.random.randint(40, 100, (4, 5))
# 将数组修改为5行4列
a1 = score.reshape([5, 4])
print(a1)
# 若行为-1，表示行不固定，根据列的大小修改，但必须保证列的大小是总数的一个因数，否则会报错
a2 = score.reshape([-1, 10])    # 元素总数为20，[-1, 10]表示 20/10 修改为2行10列
print(a2)

• resize(shape[,order]) 无返回，改变原数组，行列顺序不变

# 将数组修改为5行4列
score.resize([5, 4])
print(score)

• T 返回一个新数组，原数组不变，行列顺序改变

print(score.T)

修改数组类型

astype(dtype)

# 生成一个4行5列的随机数组，范围在[1,5) 类型为浮点型
score = np.random.uniform(1, 5, (4, 5))
# 修改数组类型为int
print(score.astype(np.int_))

数组去重

np.unique()

arr = np.array([[1, 2, 3, 4], [3, 4, 5, 6]])
print(np.unique(arr))
# [1 2 3 4 5 6]

3. ndarray运算

逻辑运算

• 大于、小于直接进行比较
• bool赋值，通过布尔索引进行赋值

arr = np.random.normal(0.75, 1, (3, 4))
print(arr)
# 逻辑判断 如果值大于0，标记为True，否则为False
print(arr > 0)  # 大于、小于 直接进行比较
# bool赋值，通过布尔索引进行赋值
arr[arr > 0] = 2    # 将大于0的元素赋值为2
print(arr)
# [[ 1.61640357 -0.21286798  0.67147044  1.07099177]
#  [ 0.87844707 -0.30592255  2.51825124 -0.53368643]
#  [ 0.85427772 -1.21688459 -0.81051012  0.77601911]]
# [[ True False  True  True]
#  [ True False  True False]
#  [ True False False  True]]
# [[ 2.         -0.21286798  2.          2.        ]
#  [ 2.         -0.30592255  2.         -0.53368643]
#  [ 2.         -1.21688459 -0.81051012  2.        ]]

通用判断函数

• np.all() 所有元素都满足才会返回True
• np.any() 任何一个元素满足都会返回True

# 通用判断函数
arr = np.random.normal(0.75, 1, (3, 4))
print(arr)
# np.all()  所有元素都满足才会返回True
print(np.all(arr > 0))
# np.any()  任何一个元素满足都会返回True
print(np.any(arr > 0))

# [[ 2.96745424  1.13869564  2.42304826  1.00264569]
#  [ 1.09160352  1.67433992  0.80692908  0.87226686]
#  [-0.11395954 -0.10808592  2.67034408  1.06746313]]
# False
# True

三元运算符

• np.where(表达式, value1, value2) 表达式为True，执行value1， 否则执行value2
• 复合逻辑需要结合 np.logical_and() 或 np.logical_or() 使用

# 三元运算符
arr = np.random.normal(0.75, 1, (3, 4))
print(arr)
# np.where(表达式, value1, value2)     表达式为True，执行value1， 否则执行value2
print(np.where(arr > 0, 1, 0))
# 复合逻辑需要结合 np.logical_and() 或 np.logical_or() 使用
print(np.where(np.logical_and(arr > 0.5, arr < 1), 1, 0))   # 大于0.5并且小于1
print(np.where(np.logical_or(arr > 0.5, arr < -0.5), 1, 0))   # 大于0.5或者小于-0.5
# [[-0.55217725  1.50314214  0.35100255  1.76121231]
#  [-0.47892572  1.7304177   1.19885493  0.28415964]
#  [ 0.83477297  0.76201994  0.40926624  0.95691155]]
# [[0 1 1 1]
#  [0 1 1 1]
#  [1 1 1 1]]
# [[0 0 0 0]
#  [0 0 0 0]
#  [1 1 0 1]]
# [[1 1 0 1]
#  [0 1 1 0]
#  [1 1 0 1]]

统计运算

• min() 最小值
• max() 最大值
• mean() 均值
• std() 标准差
• var() 方差
• argmin() 最小值的下标
• argmax() 最大值的下标

统计时，还可以指定统计轴axis（行或者列），在每个轴上进行统计, axis轴的取值并不固定，在本例中，axis 0表示列，1表示行

arr = np.random.normal(0.75, 1, (3, 4))
print(arr)
print(np.max(arr))  # 最大值
print(np.max(arr, axis=1))  # 每行的最大值
# [[ 0.25961034  0.56145924  0.71150806 -0.17447214]
#  [ 0.70701591 -0.16176053  0.24923484  0.48678436]
#  [ 1.21328659 -0.15891988  1.69161668  1.42672955]]
# 1.6916166794484437
# [0.71150806 0.70701591 1.69161668]

数组运算

数组与标量运算

• 对应元素直接进行运算

arr = np.array([1, 0, 5])
print(arr)
print(arr + 2)
print(arr * 2)
# [1 0 5]
# [3 2 7]
# [ 2  0 10]

数组与数组运算

• 数组之间的运算需要满足广播机制才可以运算，两个条件
  • 维度相等
  • shape（其中相对应的一个地方为1）

条件可以表示为：

可以运算：
A       (3d array): 5 x 4 x 7
B       (3d array): 5 x 1 x 1
Result  (3d array): 5 x 4 x 7

A       (4d array): 9 x 1 x 7 x 1
B       (3d array):     8 x 1 x 5
Result  (4d array): 9 x 8 x 7 x 5

A       (2d array): 5 x 4
B       (1d array):     1
Result  (2d array): 5 x 4

不可以运算：
A       (1d array): 10
B       (1d array): 12
A       (2d array): 2 x 1
B       (3d array): 4 x 3 x 2

arr = np.array([1, 0, 5])
arr2 = np.array([2, 1, 1, 4])
print(arr + arr2)
# ValueError: operands could not be broadcast together with shapes (3,) (4,)

a = np.array([[1, 2, 3, 2, 1, 4]])  # A         (2d array):     1 x 6
b = np.array([[[1], [3], [4]]])     # B         (3d array): 1 x 3 x 1
                                    # Result    (3d array): 1 x 3 x 6
print(a + b , '新数组的shade是{}'.format((a+b).shape))
# [[[2 3 4 3 2 5]
#   [4 5 6 5 4 7]
#   [5 6 7 6 5 8]]] 新数组的shade是(1, 3, 6)

4. matrix 矩阵介绍

矩阵和向量

• 矩阵（matrix），和数组的区别：矩阵只能是二维的，数组可以是多维的
  $$A=\left[\begin{array}{cc}1& 2\\ 3& 4\\ 5& 6\end{array}\right]\text{这是个3 × 2的矩阵，即3行2列}$$
• 向量：向量是一种特殊的矩阵，一般都是列向量
  $$B=\left[\begin{array}{c}1\\ 0\\ 4\end{array}\right]$$

加法和常量乘法

• 矩阵的加法：行列数相等才能相加
  
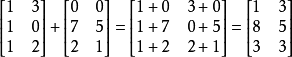
• 矩阵的常量乘法：每个元素都要乘
  $$3\times \left[\begin{array}{cc}1& 2\\ 3& 4\\ 5& 6\end{array}\right]=\left[\begin{array}{cc}3& 6\\ 9& 12\\ 15& 18\end{array}\right]$$

矩阵间的乘法

• 两个矩阵相乘，只有第一个矩阵的列数等于第二个矩阵的行数才能相乘，即：(M行，N列) × (N行，L列) = (M行，L列)
  
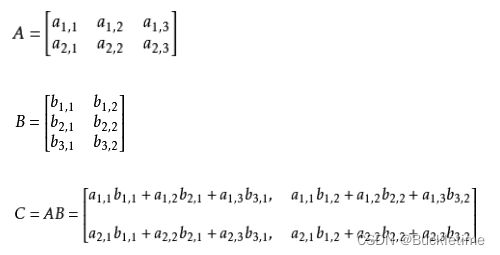
• 矩阵乘法的性质
  • (1)　结合律： (AB)C=A(BC)
  • (2)　分配律：（左分配律）C(A+B)=CA+CB
    　　　　　　　　（右分配律）(A+B)C=AC+BC
  • (3)　对常量的结合性：k(AB)=(kA)B=A(kB)

单位矩阵

• 从左上角到右下角的对角线均为1，其余元素都为0的矩阵

逆矩阵

• 矩阵A × 矩阵B = 单位矩阵，则A和B互为逆矩阵

转置矩阵

• 行和列互换的矩阵

5. Python中矩阵运算

• np.matmul() 两个矩阵相乘
• np.dot() 两个矩阵相乘或者矩阵与标量相乘

arr1 = np.random.randint(1, 7, (3, 2)) # 3 x 2 矩阵
arr2 = np.random.randint(2, 5, (2, 4)) # 2 x 4 矩阵
print(arr1)
print(arr2)
print(np.matmul(arr1, arr2))  # 结果为 3 x 4 矩阵
# print(np.dot(arr1, arr2))

# np.dot() 支持与标量相乘
print(np.dot(arr1, 5))  # 结果为 3 x 2 矩阵
# [[6 5]
#  [2 1]
#  [5 1]]
# [[2 2 3 4]
#  [4 2 3 2]]
# [[32 22 33 34]
#  [ 8  6  9 10]
#  [14 12 18 22]]
# [[30 25]
#  [10  5]
#  [25  5]]

扩展：正态分布简介

正态分布是一种概率分布。正态分布是具有两个参数μ和σ²的连续型随机变量的分布，第一参数μ是服从正态分布的随机变量的均值，第二个参数σ²是此随机变量的方差，所以正态分布记作N（μ，σ²）

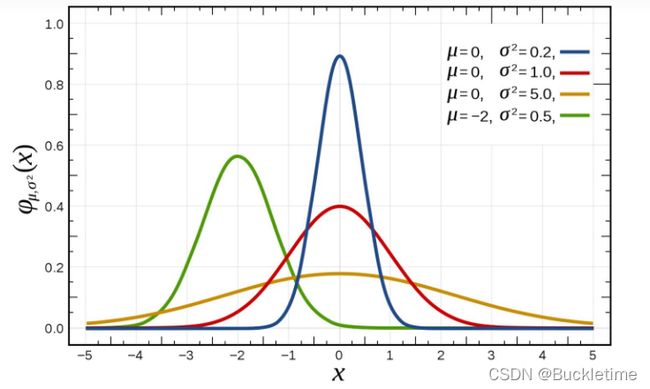
正态分布图

• 均值：图形的左右位置
• 方差：图形是瘦还是胖
  • 方差越小，图形越瘦高，数据越集中
  • 方差越大，图形越矮胖，数据越分散

方差

• 方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。
• $$s^2=\frac{{\sum }_{i=1}^n(x_i-\bar{x}{)}^2}{n}，x_i表示样本数据，\bar{x}表示样本数据平均值，n表示样本总个数$$