数据结构与算法一：时间频度和时间复杂度
数据结构系列博客涉及内容：
一、初识数据结构和算法：
1.数据结构：
- 数据结构：是相互之间存在一种或多种关系的数据元素的集合
- 研究什么：数据的逻辑结构与物理结构以及它们之间的相互关系
- 数据结构包括：线性结构和非线性结构
1.1 线性结构：
线性结构作为最常用的数据结构，其特点数据元素之间满足唯一的线性关系，每个数据元素(除第一个和最后一个外)只有一个直接前趋和一个直接后继;
线性结构拥有两种不同的存储结构，即顺序存储结构和链式存储结构。顺序存储的线性表称为顺序表，顺序表中的存储元素是
连续的，链式存储的线性表称为链表，链表中的存储元素不一定是连续的，元素节点中存放数据元素以及相邻元素的地址信息;
线性结构中存在两种操作受限的使用场景，即队列和栈。栈的操作只能在线性表的一端进行，就是我们常说的先进后出（FILO），
队列的插入操作在线性表的一端进行而其他操作在线性表的另一端进行，先进先出（FIFO），由于线性结构存在两种存储结构，
因此队列和栈各存在两个实现方式;
一维数组、链表、队列、栈
1.2 非线性结构：
- 逻辑特征是一个结点元素可能有多个直接前趋和多个直接后继。
二维数组、多维数组、广义表、树、图
算法的优劣可以用空间复杂度与时间复杂度来衡量。
1.3 度量算法的执行时间：
度量一个算法执行时间有两种方法：
- 事后统计法（运行完，进行统计，受环境影响）
- 事前估算法（时间复杂度）
统计某个算法的时间复杂度来度量方法的优越
时间复杂度统计法属于事前估算法
1.4 时间频度T(n)（代码执行行数）：
一个算法中的语句执行次数称为语句频度或时间频度，记为T(n)，n称为问题的规模。
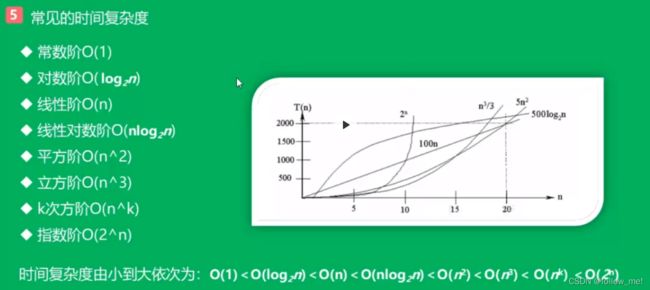
1.5 时间复杂度O(f(n)) :
某个函数f(n),使得当n趋近与无穷大时，T(n)/f(n)的极限值为不等于0的常数，这称f(n)是T(n)的同数量级函数（废话）。记作T(n)= O(f(n))
称O(f(n)) 为算法的渐进时间复杂度，简称时间复杂度
1.6 最坏时间复杂度:
最坏的情况
1.7 平均时间复杂度:
指所有可能的输入实例均以等概率情况下，该算法的运行时间。
1.8 空间复杂度（不太重要）:
算法消耗的存储空间的大小，从用户的体验上，更加注重程序执行速度，一些缓存产品（redis，memcache）和算法（计数排序）本质上就是用空间换时间。
1.9 时间复杂度的计算：
举例：
忽略常量
忽略低次项
忽略最高阶项的系数
1.10 常见的时间复杂度：
-
常数阶O(1):
无论多少行，只要没有循环、递归等复杂结构，那么这个代码的时间复杂度就都是O(1)；如下：
-
对数阶O(logn)：
其实也就是每次都乘以或者除以一个数，就是对数；如下：
-
线性阶O(n)：
for循环里面的代码会执行n遍，如下：
-
线性对数阶O(nlogn)：
将对数阶O(logn)循环N遍的话，那么它的时间复杂度就是n*O(logn),也就是O(nlogn);如下：
- 平方阶O(n^2)：
如果把O(n)的代码再循环一次，就是O(n^2)；如下：
- k次方阶O(n^K)：
O(n^3)相当于三层n循环
O(n^K)相当于K次循环
数据结构与算法更多相关内容【持续更新中】：
- 【数据结构与算法一：时间频度和时间复杂度】: 传送门.
- 【数据结构与算法二：数组】: 传送门.
- 【数据结构与算法三：栈和队列】: 传送门.
- 【数据结构与算法四：链表】: 传送门.
- 【数据结构与算法五：哈希表-哈希函数设计原则-哈希冲突解决方案】: 传送门.