【机器学习】梯度下降与正规方程(附例题代码)
文章目录
-
-
- 梯度下降
-
- 多元梯度下降法
-
- 梯度下降运算(特征放缩法)
- 多元梯度下降学习率的选择
- 多项式回归
- 多元梯度下降代码
- 正规方程
-
-
- 正规方程代码
-
- 梯度下降与正规方程的选择
-
梯度下降
对于代价函数 J ( θ 0 , θ 1 ) J(θ_0,θ_1) J(θ0,θ1),或者我们可以推广到更一般的代价函数(系数更多),如 J ( θ 0 , θ 1 , θ 2 , . . . , θ n ) J(θ_0,θ_1,θ_2,...,θ_n) J(θ0,θ1,θ2,...,θn),如果要最小化代价函数 m i n min min J ( θ 0 , θ 1 , θ 2 , . . . , θ n ) J(θ_0,θ_1,θ_2,...,θ_n) J(θ0,θ1,θ2,...,θn),那么我们可以用梯度下降法来解决,下面会以两个参数的代价函数为例对梯度下降法进行介绍:
- 给 J ( θ 0 , θ 1 ) J(θ_0,θ_1) J(θ0,θ1)的两个参数 θ 0 θ_0 θ0和 θ 1 θ_1 θ1赋两个初始值,这个值可以随意,但通常会选择将 θ 0 θ_0 θ0和 θ 1 θ_1 θ1均设为0。
- 不停地一点点改变 θ 0 θ_0 θ0和 θ 1 θ_1 θ1,使代价函数 J ( θ 0 , θ 1 ) J(θ_0,θ_1) J(θ0,θ1)越来越小,直到找到最小值。
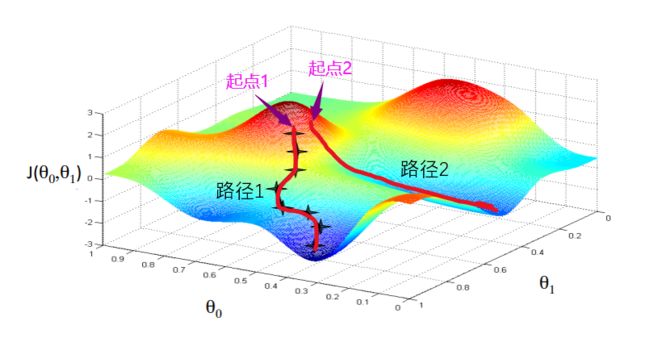
以下图为例,我们初始设定的 θ 0 θ_0 θ0和 θ 1 θ_1 θ1对应图中的某个点,我们将这个点记为起点1,现在从起点1出发,沿路径1收敛于局部的最低点,也就是局部最优解。如果我们的起点往右偏移一点得到起点2,那么第二个局部最优解应该是沿路径2收敛的最小值。同理,如果起点1往右偏移一点,也会得到不同的最优解。
下面我们来看看梯度下降算法的数学原理:
重复下面这行算法,不断更新参数 θ j θ_j θj,直到收敛于最小值,其中 : = := :=表示赋值, α α α表示学习率(learning rate),这里表示梯度下降的快慢, ∂ ∂ θ j J ( θ 0 , θ 1 ) \frac{∂}{∂θ_j}J(θ_0,θ_1) ∂θj∂J(θ0,θ1)是导数项,先不用管,之后会进行详细解释
θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) ( f o r j = 0 a n d j = 1 ) θ_j:=θ_j-α\frac{∂}{∂θ_j}J(θ_0,θ_1) \quad(for \ j=0\ and\ j=1) θj:=θj−α∂θj∂J(θ0,θ1)(for j=0 and j=1)
上面我们说到了要不断改变 θ 0 θ_0 θ0和 θ 1 θ_1 θ1的值,那么如何改变呢,也是利用上面这一行算法,并且改变 θ 0 θ_0 θ0和 θ 1 θ_1 θ1的值是同步进行的,在每次循环中,我们只要保存 θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) θ_j-α\frac{∂}{∂θ_j}J(θ_0,θ_1) θj−α∂θj∂J(θ0,θ1)的值,赋值给 θ 0 θ_0 θ0和 θ 1 θ_1 θ1即可,如下:
t e m p 0 : = θ 0 − α ∂ ∂ θ 0 J ( θ 0 , θ 1 ) temp0:=θ_0-α\frac{∂}{∂θ_0}J(θ_0,θ_1) temp0:=θ0−α∂θ0∂J(θ0,θ1)
t e m p 1 : = θ 1 − α ∂ ∂ θ 1 J ( θ 0 , θ 1 ) temp1:=θ_1-α\frac{∂}{∂θ_1}J(θ_0,θ_1) temp1:=θ1−α∂θ1∂J(θ0,θ1)
θ 0 : = t e m p 0 θ_0:=temp0 θ0:=temp0
θ 1 : = t e m p 1 θ_1:=temp1 θ1:=temp1
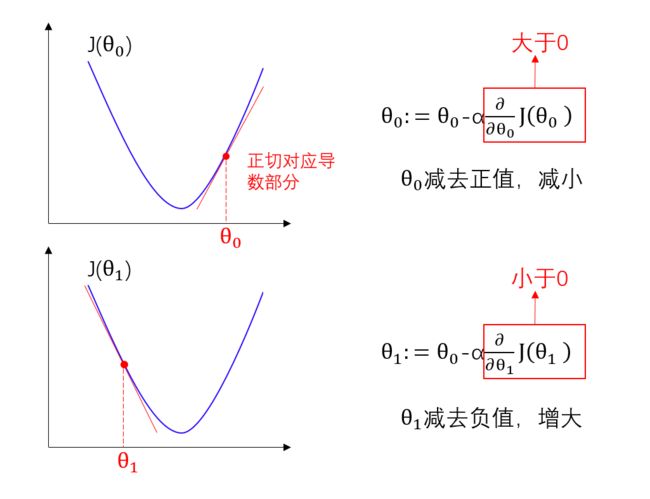
好了,现在我们来解释一下导数项 ∂ ∂ θ j J ( θ 0 , θ 1 ) \frac{∂}{∂θ_j}J(θ_0,θ_1) ∂θj∂J(θ0,θ1)的含义,假如下图所示是 J ( θ 0 ) J(θ_0) J(θ0)和 J ( θ 0 ) J(θ_0) J(θ0)的图像,我们先看看 J ( θ 0 ) J(θ_0) J(θ0),假设 θ 0 θ_0 θ0位于图中所示位置,对应点的正切值为正,那么 θ 0 θ_0 θ0将不断减小,逐渐收敛于局部最低点,当正切为0时, θ 0 θ_0 θ0不再改变,此时找到了局部最优解。
同理我们看看 J ( θ 1 ) J(θ_1) J(θ1)的图像,假设 θ 1 θ_1 θ1位于图中所示位置,对应点的正切值为负,那么 θ 1 θ_1 θ1将不断增大,逐渐收敛于局部最低点,当正切为0时, θ 1 θ_1 θ1不再改变,此时找到了局部最优解。
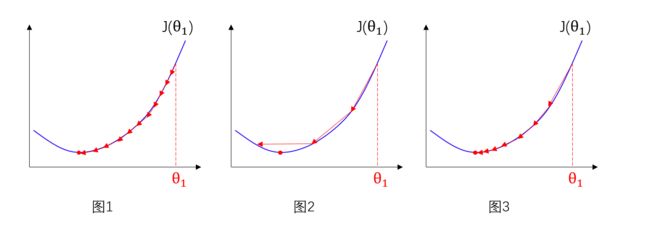
现在我们再来讨论一下公式中的 α α α, α α α表示学习率,也叫步长,下面我们以 θ 1 θ_1 θ1为例解释,可能有的同学会觉得如果 α α α取值过小, θ 1 θ_1 θ1变化的越慢,会影响效率,如图1,但如果 α α α取值过大, θ 1 θ_1 θ1每次变化的跨度很大,也可能很难找到局部最优,如图2,其实这些都不用担心,正确的梯度下降算法运行方式应该如图3,什么?越接近局部最优时步长 α α α变小了?难道还要不断改变 α α α的大小吗,其实不是 α α α变小了,而是导数项 ∂ ∂ θ j J ( θ 0 , θ 1 ) \frac{∂}{∂θ_j}J(θ_0,θ_1) ∂θj∂J(θ0,θ1)变小了,我们都知道在收敛于局部最优的过程中,正切值是不断收敛于0的,因此 α ∂ ∂ θ 1 J ( θ 0 , θ 1 ) α\frac{∂}{∂θ_1}J(θ_0,θ_1) α∂θ1∂J(θ0,θ1)整体是减小的,所以越趋近于局部最优, θ 1 θ_1 θ1的改变量自然会越来越小,并不用额外去改变 α α α的大小。
ok,现在我们知道了 θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) ( f o r j = 0 a n d j = 1 ) θ_j:=θ_j-α\frac{∂}{∂θ_j}J(θ_0,θ_1) \quad(for\ j=0\ and\ j=1) θj:=θj−α∂θj∂J(θ0,θ1)(for j=0 and j=1)这行算法的含义,那么要写出代码,我们还需要求出导数项 ∂ ∂ θ j J ( θ 0 , θ 1 ) \frac{∂}{∂θ_j}J(θ_0,θ_1) ∂θj∂J(θ0,θ1),才可以实现最小化代价函数
已知代价函数:
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h 0 ( x ( i ) ) − y ( i ) ) 2 J(θ_0,θ_1)=\frac{1}{2m}\sum^{m}_{i=1}(h_0(x^{(i)})-y^{(i)})^2 J(θ0,θ1)=2m1i=1∑m(h0(x(i))−y(i))2
对代价函数求偏导:
∂ ∂ θ j J ( θ 0 , θ 1 ) = ∂ ∂ θ j 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 \frac{∂}{∂θ_j}J(θ_0,θ_1)=\frac{∂}{∂θ_j}\frac{1}{2m}\sum^{m}_{i=1}(h_θ(x^{(i)})-y^{(i)})^2 ∂θj∂J(θ0,θ1)=∂θj∂2m1i=1∑m(hθ(x(i))−y(i))2
= ∂ ∂ θ j 1 2 m ∑ i = 1 m ( θ 0 − θ 1 x ( i ) − y ( i ) ) 2 =\frac{∂}{∂θ_j}\frac{1}{2m}\sum^{m}_{i=1}(θ_0-θ_1x^{(i)}-y^{(i)})^2 =∂θj∂2m1i=1∑m(θ0−θ1x(i)−y(i))2
因此对于 j = 0 j=0 j=0和 j = 1 j=1 j=1分别有:
∂ ∂ θ 0 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h 0 ( x ( i ) ) − y ( i ) ) \frac{∂}{∂θ_0}J(θ_0,θ_1)=\frac{1}{m}\sum^{m}_{i=1}(h_0(x^{(i)})-y^{(i)}) ∂θ0∂J(θ0,θ1)=m1i=1∑m(h0(x(i))−y(i))
∂ ∂ θ 1 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h 0 ( x ( i ) ) − y ( i ) ) x ( i ) \frac{∂}{∂θ_1}J(θ_0,θ_1)=\frac{1}{m}\sum^{m}_{i=1}(h_0(x^{(i)})-y^{(i)})x^{(i)} ∂θ1∂J(θ0,θ1)=m1i=1∑m(h0(x(i))−y(i))x(i)
现在我们求得了偏导,将偏导代回原来的式子,得到如下算法,不断重复更新 θ 0 θ_0 θ0和 θ 1 θ_1 θ1,直到收敛即可:
θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h 0 ( x ( i ) ) − y ( i ) ) θ_0:=θ_0-α\frac{1}{m}\sum^{m}_{i=1}(h_0(x^{(i)})-y^{(i)}) θ0:=θ0−αm1i=1∑m(h0(x(i))−y(i))
θ 1 : = θ 1 − α 1 m ∑ i = 1 m ( h 0 ( x ( i ) ) − y ( i ) ) x ( i ) θ_1:=θ_1-α\frac{1}{m}\sum^{m}_{i=1}(h_0(x^{(i)})-y^{(i)})x^{(i)} θ1:=θ1−αm1i=1∑m(h0(x(i))−y(i))x(i)
多元梯度下降法
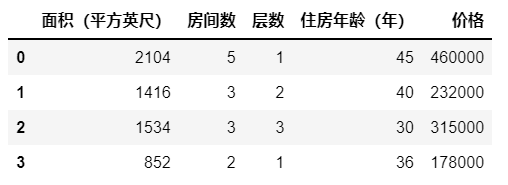
例题:分析住房价格与所给特征值 x 1 , x 2 , x 3 , x 4 x_1,x_2,x_3,x_4 x1,x2,x3,x4的关系
| 面积(平方英尺) | 房间数 | 层数 | 住房年龄(年) | 价格($1000) |
|---|---|---|---|---|
| x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | x 4 x_4 x4 | y y y |
| 2104 | 5 | 1 | 45 | 460 |
| 1416 | 3 | 2 | 40 | 232 |
| 1534 | 3 | 2 | 30 | 315 |
| 852 | 2 | 1 | 36 | 178 |
注:
- n表示特征值的个数,如这里的x有四个,故n=4
- m表示样本数目,一行为一个样本,m=4
- x ( i ) x^{(i)} x(i)表示第i个训练样本的输入特征值,如:
x ( 2 ) = [ 1416 3 2 40 ] x^{(2)}=\left[ \begin{matrix} 1416 \\ 3 \\ 2 \\ 40 \end{matrix} \right] x(2)=⎣⎢⎢⎡14163240⎦⎥⎥⎤
- x j ( i ) x^{(i)}_j xj(i)表示第i个训练样本中第j个特征量的值
在之前的回归假设中,我们假设的函数 h θ ( x ) = θ 0 + θ 1 x h_θ(x)=θ_0+θ_1x hθ(x)=θ0+θ1x只有一个元,在多元问题中,这个假设不再适用,由于有四个特征值,我们可以假设成 h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + θ 4 x 4 h_θ(x)=θ_0+θ_1x_1+θ_2x_2+θ_3x_3+θ_4x_4 hθ(x)=θ0+θ1x1+θ2x2+θ3x3+θ4x4
现在利用矩阵来简化一下这个等式的表示方式,为了统一形式, θ 0 θ_0 θ0看成 θ 0 x 0 θ_0x_0 θ0x0,令 x 0 = 1 x_0=1 x0=1即可,那么现在也就意味着第 i i i个都有一个向量 x ( i ) x^{(i)} x(i),其中 x 0 ( i ) = 1 x^{(i)}_0=1 x0(i)=1,由于特征值x加多了一列,所以特征向量 x x x是一个从0开始的 n + 1 n+1 n+1维向量
x = [ x 0 x 1 x 2 x 3 x 4 ] ∈ R n + 1 θ = [ θ 0 θ 1 θ 2 θ 3 θ 4 ] ∈ R n + 1 x=\left[ \begin{matrix} x_0 \\ x_1 \\ x_2 \\ x_3\\x_4 \end{matrix} \right] ∈R^{n+1}\\ θ=\left[ \begin{matrix} θ_0 \\ θ_1 \\ θ_2 \\ θ_3\\θ_4 \end{matrix} \right] ∈R^{n+1} x=⎣⎢⎢⎢⎢⎡x0x1x2x3x4⎦⎥⎥⎥⎥⎤∈Rn+1θ=⎣⎢⎢⎢⎢⎡θ0θ1θ2θ3θ4⎦⎥⎥⎥⎥⎤∈Rn+1
有了上面这两个矩阵,我们假设的函数就可以用矩阵进行表示了,如下:
h θ ( x ) = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + θ 4 x 4 = θ T x h_θ(x)=θ_0x_0+θ_1x_1+θ_2x_2+θ_3x_3+θ_4x_4=θ^{T}x hθ(x)=θ0x0+θ1x1+θ2x2+θ3x3+θ4x4=θTx
现在,我们来看看多元梯度下降算法的运作形式:
首先,我们把参数看成 n + 1 n+1 n+1维向量,则代价函数 J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(θ)=\frac{1}{2m}\sum^m_{i=1}(h_θ(x^{(i)})-y^{(i)})^2 J(θ)=2m1∑i=1m(hθ(x(i))−y(i))2
然后重复以下这行算法,直到收敛于局部最优解:
θ j : = θ j − α ∂ ∂ θ j J ( θ ) ( f o r j = 0 , . . . , n ) θ_j:=θ_j-α\frac{∂}{∂θ_j}J(θ) \quad(for\ j=0,...,n) θj:=θj−α∂θj∂J(θ)(for j=0,...,n)
这里的导数项 α ∂ ∂ θ j J ( θ ) = α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) α\frac{∂}{∂θ_j}J(θ)=α\frac{1}{m}\sum^m_{i=1}(h_θ(x^{(i)})-y^{(i)})x^{(i)}_j α∂θj∂J(θ)=αm1∑i=1m(hθ(x(i))−y(i))xj(i),因此变成:
θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) ( f o r j = 0 , . . . , n ) θ_j:=θ_j-α\frac{1}{m}\sum^m_{i=1}(h_θ(x^{(i)})-y^{(i)})x^{(i)}_j\quad(for \ j=0,...,n) θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i)(for j=0,...,n)
梯度下降运算(特征放缩法)
但一个问题含有多个特征值,如果能保证不同特征的取值在相近的范围内,梯度下降法就能更快地收敛,还是以上面的例题为例, x 1 x_1 x1表示面积,取值在02000平方英尺**之间,$x_2$表示房间数,**取值在05之间,现在特征值间的差距还是很大的,我们要尽量将特征值的范围约束在 [ − 1 , 1 ] [-1,1] [−1,1]的范围内,只需进行如下标准化在操作:
x ′ = x − x ‾ σ x'=\frac{x-\overline{x}}{σ} x′=σx−x
x ‾ \overline{x} x是平均值, σ σ σ是标准差。
多元梯度下降学习率的选择
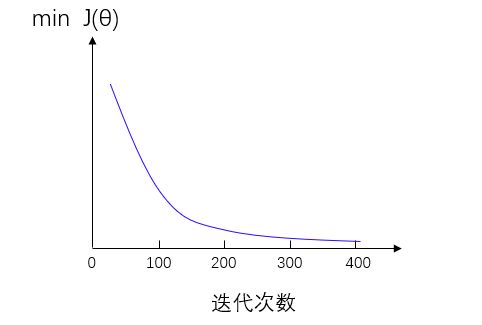
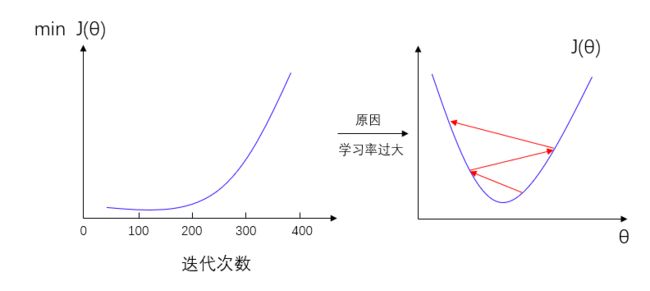
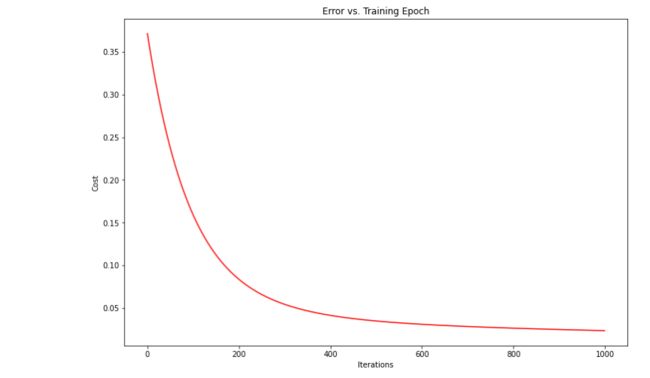
对于学习率的选择,我们可以先在梯度下降算法运行时绘制出代价函数 J ( θ ) J(θ) J(θ)和迭代次数的图来评估算法的运行是否正常,若算法运行正常,则图像呈现出来的是在每一步迭代之后 J ( θ ) J(θ) J(θ)都在下降,最终趋于稳定,也就是梯度下降算法已经收敛,如下图:
如果学习率过大,会出现下图代价函数不收敛反而发散的情况,这时候需要减小学习率
其实只要学习率足够小,那么每次迭代之后代价函数 J ( θ ) J(θ) J(θ)都会下降,所以如果出现的曲线不是下降的,一般都认为是学习率过大。但学习率过小,收敛速率会很低。
所以在算法运行时,我们会尝试不同的学习率,比如 0.001 , 0.01 , 0.1 , 1 , . . . 0.001,0.01,0.1,1,... 0.001,0.01,0.1,1,...然后对于这些不同的 α α α值绘制 J ( θ ) J(θ) J(θ)随迭代步数变化的曲线,然后选择使得 J ( θ ) J(θ) J(θ)快速下降的一个 α α α值。
多项式回归
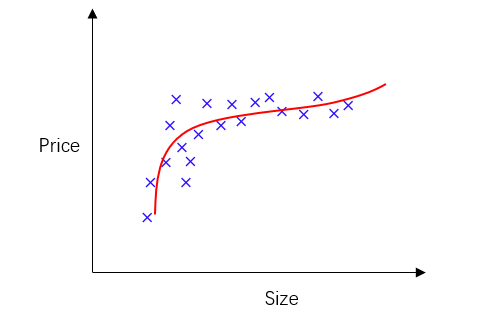
有时候,我们要拟合的不是简单的直线,也可能是曲线,这时候就要选择多项式模型进行拟合,如下图表示房价与面积的关系,我们根据散点图的特征可选择一个三次函数去进行拟合,如 θ 0 + θ 1 x + θ 2 x 2 + θ 3 x 3 θ_0+θ_1x+θ_2x^2+θ_3x^3 θ0+θ1x+θ2x2+θ3x3,大致如图中红线所示,这里只是举个例子,还有很多其他多项式拟合模型也是适用的:
好了,现在拟合模型有了,接下来要做的就是将模型与我们的数据进行拟合,按照之前线性拟合的假设形式,我们可以写成:
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 h_θ(x)=θ_0+θ_1x_1+θ_2x_2+θ_3x_3 hθ(x)=θ0+θ1x1+θ2x2+θ3x3
= θ 0 + θ 1 ( s i z e ) + θ 2 ( s i z e ) 2 + θ 3 ( s i z e ) 3 =θ_0+θ_1(size)+θ_2(size)^2+θ_3(size)^3 =θ0+θ1(size)+θ2(size)2+θ3(size)3
特征值设置为:
x 1 = ( s i z e ) x 1 ∈ [ 1 , 1 0 3 ] x_1=(size) \quad x_1∈[1,10^3] x1=(size)x1∈[1,103]
x 2 = ( s i z e ) 2 x 2 ∈ [ 1 , 1 0 6 ] x_2=(size)^2 \quad x_2∈[1,10^6] x2=(size)2x2∈[1,106]
x 3 = ( s i z e ) 3 x 3 ∈ [ 1 , 1 0 9 ] x_3=(size)^3 \quad x_3∈[1,10^9] x3=(size)3x3∈[1,109]
通过上面一些简单的改变,我们就可以把多项式回归转换为了我们熟悉的线性回归,进行特征值放缩后再用梯度下降算法求解即可。
多元梯度下降代码
import numpy as np
from numpy import genfromtxt
import pandas as pd
import matplotlib.pyplot as plt
#读取数据(用的是例题数据)
data = pd.read_csv('C:\\Users\\Lenovo\\Desktop\\room.csv')
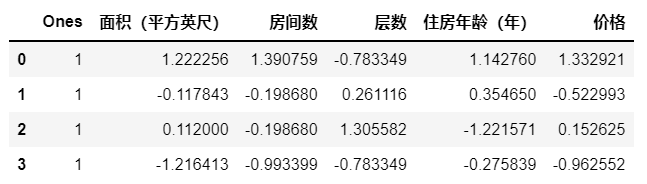
#特征值放缩
data = (data - data.mean()) / data.std()
# 增加一列1
data.insert(0, 'Ones', 1)
#数据处理
x_data = np.array(data.iloc[:, 0:-1]) #取不包含最后一列的所有数据,并转化为数组,不然不能进行下面的运算
y_data = np.array(data.iloc[:,-1]).reshape(4,1) #取最后一列数据
theta = np.array([0,0,0,0,0]).reshape(5,1) #θ参数初始化为0
#参数设置
alpha = 0.003#学习率
iternum = 1000 #最大迭代次数
m = 4 #样本数
#代价函数
def cost_function(theta,x_data,y_data):
inner = np.power((dot(x_data , theta) - y_data),2)#这里看成矩阵运算
return np.sum(inner) / (2 * m) #对数组求和除以2和样本数就是代价函数
#代价函数的偏导
def gradient_function(theta,x_data,y_data,m):
return (1/m) * dot(x_data.transpose(), (dot(x_data , theta) - y_data))#这是对代价函数求偏导后的结果
#核心算法,梯度下降
def gradient_desent(x_data, y_data, theta, alpha, m):
gradient = gradient_function(theta,x_data,y_data ,m)
cost = np.zeros(iternum)#保存下来用于绘制学习曲线
i = 0
while not all(abs(gradient) <= 0.0001): #若偏导小于0.0001,这时相当于0,也就是正切为零,找到局部最优解
if(i >=iternum): #到达最大迭代次数,也终止迭代
break
theta = theta - alpha * gradient #更新参数的值
cost[i] = cost_function(theta,x_data,y_data) #记录每次迭代后最小化代价函数的值
i = i+1 #记录迭代次数
gradient = gradient_function(theta,x_data,y_data ,m) #更新偏导
return theta,cost
theta_end1,cost = gradient_desent(x_data, y_data, theta, alpha, m)#调用函数,求解参数
#画出代价函数与迭代次数的学习曲线,看看梯度下降是否正常运行,选择合适的学习率
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(iternum), cost, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()
正规方程
正规方程也叫最小二乘法,其实就是通过求导来确定代价函数的极小值。
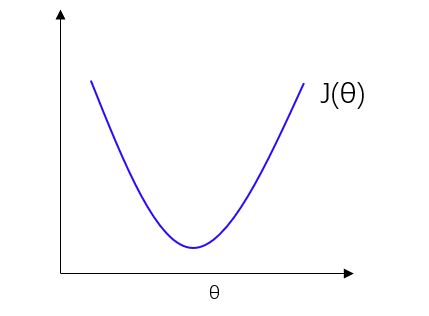
我们假设一个代价函数 J ( θ ) = a θ 2 + b θ + c J(θ)=aθ^2+bθ+c J(θ)=aθ2+bθ+c,函数图像如下图:
我们只需要对代价函数求导并令其等于0,就能解出使得 J ( θ ) J(θ) J(θ)取最小值的 θ θ θ值
同样的,当 θ θ θ是一个 n + 1 n+1 n+1维的参数向量时,对所有参数逐一求导即可:
J ( θ 0 , θ 1 , . . . , θ n ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(θ_0,θ_1,...,θ_n)=\frac{1}{2m}\sum^m_{i=1}(h_θ(x^{(i)})-y^{(i)})^2 J(θ0,θ1,...,θn)=2m1i=1∑m(hθ(x(i))−y(i))2
∂ ∂ θ j J ( θ ) = . . . = 0 ( 对 所 有 参 数 逐 一 求 导 ) \frac{∂}{∂θ_j}J(θ)=...=0\qquad(对所有参数逐一求导) ∂θj∂J(θ)=...=0(对所有参数逐一求导)
求 解 出 对 应 的 θ 0 , θ 1 , . . . , θ n 求解出对应的θ_0,θ_1,...,θ_n 求解出对应的θ0,θ1,...,θn
但如果参数太多,这样遍历求解会很耗费时间,下面再看看其他方法,还是用上面的例子做引入
| 面积(平方英尺) | 房间数 | 层数 | 住房年龄(年) | 价格($1000) |
|---|---|---|---|---|
| x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | x 4 x_4 x4 | y y y |
| 2104 | 5 | 1 | 45 | 460 |
| 1416 | 3 | 2 | 40 | 232 |
| 1534 | 3 | 2 | 30 | 315 |
| 852 | 2 | 1 | 36 | 178 |
现在我们在数据集中额外加入 x 0 x_0 x0,并令其等于1
| 面积(平方英尺) | 房间数 | 层数 | 住房年龄(年) | 价格($1000) | |
|---|---|---|---|---|---|
| x 0 x_0 x0 | x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | x 4 x_4 x4 | y y y |
| 1 | 2104 | 5 | 1 | 45 | 460 |
| 1 | 1416 | 3 | 2 | 40 | 232 |
| 1 | 1534 | 3 | 2 | 30 | 315 |
| 1 | 852 | 2 | 1 | 36 | 178 |
现在我们构建一个m×(n+1)的矩阵 X X X,和一个m维向量 y y y:
X = [ 1 2104 5 1 45 1 1416 3 2 40 1 1534 3 2 30 1 852 2 1 36 ] y = [ 460 232 315 178 ] X=\left[ \begin{matrix} 1&2104&5&1&45 \\ 1&1416&3&2&40 \\ 1&1534&3&2&30 \\ 1&852&2&1&36 \end{matrix} \right]\\ y=\left[ \begin{matrix} 460 \\ 232 \\ 315 \\ 178 \end{matrix} \right] X=⎣⎢⎢⎡11112104141615348525332122145403036⎦⎥⎥⎤y=⎣⎢⎢⎡460232315178⎦⎥⎥⎤
因此有
Y = X θ Y=Xθ Y=Xθ
但 X X X不是方阵,没有逆矩阵,不能直接求 θ θ θ,所以我们可以两边同时左乘 X T X^{T} XT,变成:
X T Y = X T X θ X^{T}Y=X^{T}Xθ XTY=XTXθ
现在 X T X X^{T}X XTX是方阵了,也是可逆的,那么就可以求得 θ θ θ
θ = ( X T X ) − 1 X T Y θ=(X^{T}X)^{-1}X^{T}Y θ=(XTX)−1XTY
正规方程代码
数据的前期处理和梯度下降一样,这里就不重复写了
#正规方程
def normalEqn(x_data,y_data):
#核心算法
theta = np.linalg.inv(np.transpose(x_data)@x_data)@np.transpose(x_data)@y_data
return theta
final_end2 = normalEqn(x_data, y_data)
梯度下降与正规方程的选择
假设有m个训练样本和n个特征值
| 梯度下降 | 正规方程 | |
|---|---|---|
| 缺点 | 需要选择学习率、需要多次迭代 | 若n很大,高维矩阵求逆会花费大量时间 |
所以当n较小时(例如以10000为界限),可选择正规方程,较大时可选择梯度下降
参考资料:
吴恩达机器学习系列课程
机器学习笔记
机器学习之多元线性回归模型梯度下降法的python实现
梯度下降算法原理讲解——机器学习