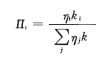复杂网络基础概念总结
前言:最近刚定下的课题,现在主要学习网络基础概念的知识,凡是学习总是得做下总结笔记才能比较清楚。也分享给大家一起学习吧,如有错误可以提出私信我或者评论。
社会网络通常显示出较强的社区效应,网络中的节点趋于形成紧密联系的群组。
社区定义:社区结构是网络顶点的组。 在这些组内有密集的内部联系,但在组之间有较少的边缘。
社区特征:社团内部连接紧密,社团之间连接相对稀疏。
社区发现/社区检测/社团检测定义:将网络节点按照其内在的拓扑结构连接紧密程度划分成若干子图的过程。
社区结构划分的意义:社区往往代表了复杂网络中具有相同或者相似功能的元素的集合,这些元素相互协作或者相互作用,共同完成整个系统中某些相对独立的功能或者组成相对独立的组织结构。提取网络中的社区结构有助于我们理解网络的拓扑结构特性、揭示复杂网络系统内在的功能特性、理解社区内个体之间的关系及演化趋势。
均匀网络
泊松分布和幂律分布对应于均匀网络和非均匀网络。
服从泊松分布的网络叫均匀网络,均匀网络和非均匀网络(无标度网络)是一个对比。
BA 无标度网络
1999 年 Barabási 和 Albert 提出了无标度网络模型(简称 BA 模型)。无标度网络的重要特征为: 无标度网络的节点度分布服从幂律分布。
近年在复杂网络研究上的另一重大发现就是许多复杂网络,包 Internet WWW 以及新陈代谢网络等的连接度分布函数具有幂律形式。由于这类网 络的节点的连接度没有明显的特征长度,故称为无标度网络
①增长 (growth) 特性 即网络的规模是不断扩大的。例如每个月都会有大量的新 的科研文章发表,而 WWW 上则每天都有大量新的网页产生。
②优先连接 (preferential attachment) 特性 即新的节点更倾向于与那些具有较高 连接度的"大"节点相连接。这种现象也称为"富者更富 (rich get richer)" 或"马太效应 (Matthew effect)" 。
BA 无标度模型构造算法
①增长 从一个具有 mo 个节点的网络开始,每次引入一个新的节点,并且连到个已存在的节点上,这里 m<:mo
②优先连接:一个新节点与一个已经存在的节点 相连接的概率![]()
与节点 i的度ki、节点j的度kj之间满足如下关系:
特征长度
幕律分布
幂律分布是指某个具有分布性质的变量,且其分布密度函数是幂函数(由于分布密度函数必然满足“归一律”,所以这里的幂函数,一般规定小于负1)的分布。
幂律分布表现为一条斜率为幂指数的负数的直线,这一线性关系是判断给定的实例中随机变量是否满足幂律的依据。
幂律分布也称为无标度 (scale- free) 分布,具有幂律度分布的网络也称为无标度网络,这是由于幂律分布函数具有如下无标度性质。即系统中个体的尺度相差悬殊,缺乏一个优选的规模。
当样本数据较多时,变量x的概率密度函数:f(x)~x^(-α-1)。
模块性
系统的模块化程度。系统中的模块内聚程度越高,模块之间耦合度越低,系统的模块性越好。
模块度(modularity)
是常用的社团划分质量评价指标,基本想法是把社团划分后的网络与相应的零模型进行比较,度量社团划分的质量。
零模型:与原网络具有相同节点数目、相同连边数目、相同度序列的随机网络。
*互信息NMI(Normalized Mutual Information )
互信息的概念大家都不陌生,它基于香农熵,衡量了两个随机变量间的依赖程度。而不同于普通的相似性度量方法,互信息可以捕捉到变量间非线性的统计相关性,因而可以认为其能度量真实的依赖性。
模体
模体是网络的基本拓扑结构之一, 它的大小介于网络个体和社团之间, 一般由少数几个节点连接构成, 模体也揭示了网络的演化规律, 它是社团内部成员之间基本的连接模式
超家族
从共同祖先进化而来、但相似性较少的一组(基因)或(蛋白质)。
自相似性
如果一个物体自我相似(Self-similarity),表示它和它本身的一部分完全或是几乎相似。
自相似包含两种,一种是部分和整体严格的相似,另一种指的是统计上的相似,比如海岸线。
层次性
(实际双向连接的边的数量)/(可能双向连接的边的数量,即C(n,2))
我们假想在一个企业的命令传达网络中,如果命令都是从上到下单向传递的,那么我们认为整个的网络很有层次,所以双向连接的数量就很少,层次度就更加接近于1。反之,如果一个企业中,A可以向B传达命令,同时B也可以对A下达命令,那么这个组织就不是那么的有层次性。
结构冗余性
模块化
网络进化
鲁棒性
鲁棒是Robust的音译,也就是健壮和强壮的意思。它也是在异常和危险情况下系统生存的能力。
在复杂网络中,如果在移走少量节点后网络中的 绝大部分节点仍是连通的,那么就称该网络的连通性对节点故障具有鲁棒性。
脆弱性
存在致命缺点
同配性(assortatvity)与异配性(disassortatvity):
在不改变节点度分布的情况下,可以使度大的节点倾向于和其它度大的节点连接。网络中的这个重要的结构特性,称之为节点之间的相关性(Correlation)。如果网络中的节点趋于和它近似的节点相连,就称该网络是同配的(Assortative);反之,就称该网络是异配的(Disassortative)。
网络同配性(或异配性)的程度可用同配系数(也称Pearson Coefficient----皮尔森系数)r来刻画。r>0表示整个网络呈现同配性结构,度大的节点倾向于和度大的节点相连;r<0表示整个网络呈现异配性;r=0表示网络结构不存在相关性
核数
一个节点的核数,就是网络在进行k核分解(k-core decomposition)是的k-shell指数。对于一个网络,0核是原图;1核就是去掉所有孤立点的图;2核就是先去掉所有度小于2的点,然后再剩下的图中再去掉度小于2的点,依次类推,直到不能去掉为止;一个节点的核数定义为这个节点所在的最大核的阶数——比如一个节点最多在5核而不在6核中,就说这个节点的核数=5。
介数
介数通常分为边介数和节点介数两种.
节点介数:为网络中所有最短路径中经过该节点的路径的数目占最短路径总数的比例.
边介数:为网络中所有最短路径中经过该边的路径的数目占最短路径总数的比例.
介数反映了相应的节点或者边在整个网络中的作用和影响力,是一个重要的全局几何量,具有很强的现实意义。
最短路径
连接两个节点最少边数的路径
平均路径长度
网络中任意两个节点之间路径长度的平均值,
度分布
度分布指的是对一个图(网络)中顶点(节点)度数的总体描述。对于随机图,度分布指的是图中顶点度数的概率分布。
集聚系数
集聚系数(也称群聚系数、集群系数)是用来描述一个图中的顶点之间集结成团的程度的系数。具体来说,是一个点的邻接点之间相互连接的程度。例如生活社交网络中,你的朋友之间相互认识的程度。
公式为一节点的边数Ei比上全部可能的边数:
![]()
全局耦合网络 (globally coupled network) 中,任意两个点之间都有边直接相
连(图 2-1 (a 门。因此,在具有相同节点数的所有的网络中,全局藕合网络具有最小的平均
路径长度 gc =l 和最大的聚类系数 =1 。
最近邻藕合网络( nearest-neighbor coupled network) ,
其中每一个节点只和它周围的邻居节点相连。真有周期边界条件的
最近邻藕合网络包含 个围成一个环的点,其中每个节点都与它左右各 K/2 个邻居点
相连,这里 是一个偶数(罔 2- l( b)) 。
星形藕合网络(star coupled network) ,它有一个中心点,
其余的 N-1 个点都只与这个中心点连接,而它们彼此之间不连接(图 2- l( c)) 。
WS小世界模型构造算法
作为从完全规则网络向完全随机图的过渡,Watts Strogtz 1998 年引人了一个有趣 的小世界网络模型,称为 WS 小世界模型。 WS 小世界模型的构造算法如下:
①从规则图开始:考虑一个含有 N 个点的最近邻耦合网络,它们围成一个环,其中每个节点都与它左右相邻的各 K/2 节点相连 ,K是偶数。
②随机化重连:以概率 P 随机地重新连接网络中的每个边,即,将边的一个端点保持不变,而另一个端点取为网络中随机选择的一个节点。其中规定,任意两个不同的节点之间至多只能有一条边,并且每一个节点都不能有边与自身相连。
NW 小世界模型构造算法
WS 小世界模型构造算法中的随机化过程有可能破坏网络的连通性。另一个研究较 多的小世界模型是由 Newman Watts 稍后提出的,称为 NW 小世界模型。
该模型是通过用"随机化加边"取代 WS 小世界模型构造中的"随机化重连"而得到的 。具体构造算法如下:
①从规则图开始:考虑一个含有 N 个点的最近邻耦合网络,它们围成一个环,其中每个节点都与它左右相邻的各 K/2 节点相连 ,K是偶数。
②随机化加边:以概率 P 在随机选取的一对节点之间加上一条边 其中,任意两个不同的节点之间至多只能有一条边,并且每一个节点都不能有边与自身相连。
适应度模型构造算法
①增长:从一个具有 m0 个节点的网络开始每次引入一个新的节点并且连到 m 个已存在的节点上,这里 m≤m0 每个节点的适应度按概率分布 ρ(η) 选取。
②优先连接:一个新节点与一个已经存在的节点 i 相连接的概率且∏,与节点 i 的度k 、节点 j 的度 kj 和适应度 ηi 之间满足如下关系
富人俱乐部 (rich-club)
Internet 中少量的节点具有大量的边,这些节点也称为"富节点 (rich nodes)"; 它们
倾向于彼此之间相互连接(图 3-11) ,构成"富人俱乐部 (rich-club)"。
待续……
如果有帮助就点个赞吧!嘻嘻~
如果有帮助就点个赞吧!嘻嘻~
如果有帮助就点个赞吧!嘻嘻~