基于二手车价格预测——特征工程

特征工程

我的理解就是在建模解决实际问题时，会在建模前收集可能与实际业务有关的特征，但这些特征可能是一些单一的特征，通过EDA发现这些特征值有异常值，缺失值等，不同的模型对特征的要求不一样，这些特征直接进入模型的效果往往不好，因此，我们需要对特征进行清洗，加工，筛选才能进入模型。
以下数据处理过程以二手车价格预测比赛为例。

分析：

不同模型对数据集的要求不同。
使用不同的模型，对数据的处理也是不同的。如使用树结构的模型，不需要处理缺失值，因为树模型可以处理缺失值。对于svm,LR等模型就需要特征归一化处理，会涉及距离计算的模型如线性回归，SVM等，如果入模的特征在量纲上不相等，在计算距离时量纲大的特征会决定模型的结果。

第一步：异常值处理

异常值处理方法有很多
如3西格玛法，箱型图，孤立森林等

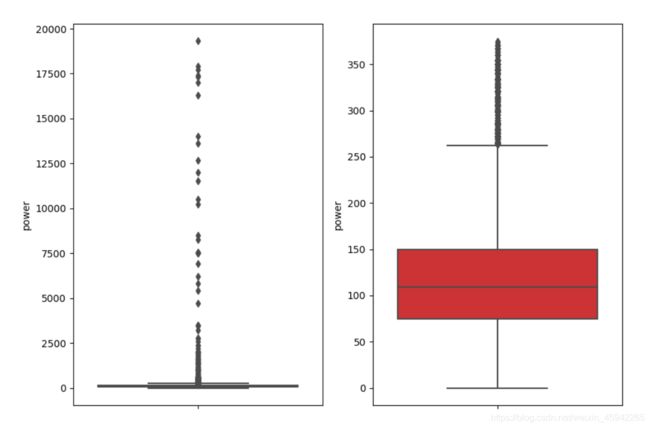
箱型图法：

中位数：假设n是奇数，则中位数是位于中间的数值，如果n是偶数，则中位数就是中间两个数的平均值。

中位数举个例子：
现在有4个人，工资从高到低排列以后，分别是10,11,12,13万，中间的两个数是11和12，所以中位数就是11+12=11.5万，当马云进来一起的时候，5个人中的中间位置是12万，所以中位数是12万，所以即使是马云这样的超级富豪计入数据集里面，中位数还是可以正确的描述这批数据的整体收入水平，不会像平均值那样因为异常的数据产生变化。

四分位数和中位数比较相似，箱型图可以很好的将四分位数的结构可视化出来，下界和上界表示数据集最小值和最大值，下四分位数0.25就是离下界近的第25%个数，其次是中位数，然后是上四分位数0.75，上四分位数减去下四分位数就是四分位距离。
四分位距离越小，表示中间的50%的数据越集中，中位数就更能代表整体水平

计算用四分位距离乘以箱线图尺度，一般将箱线图尺度设置为1.5，有时候也设置为3
公式

val_low=Q1-1.5ΔQ
val_up=Q3+1.5ΔQ
Q1表示下四分位，Q3表示上四分位，△Q表示四分位距离（参考资料）1.5处是异常值隔断点，称其为内限，3处是外限，内限和外限之间是温和异常值，外限以外就是极端的异常值。

代码：

def outliers_proc(data, col_name, scale=3):
    """
         用于清洗异常值，默认用 box_plot（scale=3）进行清洗
         :param data: 接收 pandas 数据格式
         :param col_name: pandas 列名
         :param scale: 尺度
         :return:
    """ 
    def box_plot_outliers(data_ser, box_scale):
        """
        利用箱线图去除异常值
        :param data_ser: 接收 pandas.Series 数据格式
        :param box_scale: 箱线图尺度，
        :return:
        """
        iqr = box_scale * (data_ser.quantile(0.75) - data_ser.quantile(0.25))
        val_low = data_ser.quantile(0.25) - iqr
        val_up = data_ser.quantile(0.75) + iqr
        rule_low = (data_ser < val_low)
        rule_up = (data_ser > val_up)
        return (rule_low, rule_up), (val_low, val_up)

    data_n = data.copy()
    data_series = data_n[col_name]
    rule, value = box_plot_outliers(data_series, box_scale=scale)
    index = np.arange(data_series.shape[0])[rule[0] | rule[1]]
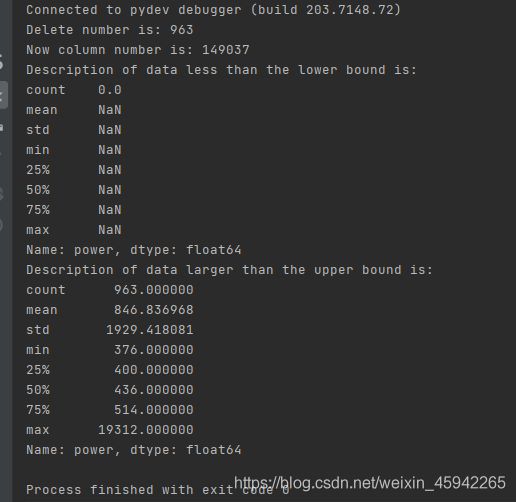
    print("Delete number is: {}".format(len(index)))
    data_n = data_n.drop(index)
    data_n.reset_index(drop=True, inplace=True)
    print("Now column number is: {}".format(data_n.shape[0]))
    index_low = np.arange(data_series.shape[0])[rule[0]]
    outliers = data_series.iloc[index_low]
    print("Description of data less than the lower bound is:")
    print(pd.Series(outliers).describe())
    index_up = np.arange(data_series.shape[0])[rule[1]]
    outliers = data_series.iloc[index_up]
    print("Description of data larger than the upper bound is:")
    print(pd.Series(outliers).describe())

    fig, ax = plt.subplots(1, 2, figsize=(10, 7))
    sns.boxplot(y=data[col_name], data=data, palette="Set1", ax=ax[0])
    sns.boxplot(y=data_n[col_name], data=data_n, palette="Set1", ax=ax[1])
    return data_n

处理后：

第二步：特征构造

特征构造这一步我觉得是非常关键的一步，通过不同特征之间的组合，我们就可以获得一些高级的特征，这些特征往往覆盖了更多的信息。

特征组合的方法有：
1.构造统计量特征，最大值，最小值，中位数，均值，标准差，计数，求和，比例；
2.时间特征，包括相对时间差，节假日和休息日；相对时间差也可以进行分组；统计时间可按照白天/晚上、淡旺季进行分组；
3.地理特征，分箱编码；
4.非线性变化，取log/平方/开方
5.特征组合，特征转换

在本项目中通过：
汽车上架时间（creatDate)和汽车注册车牌时间（regDate)之间的差值可以构造汽车使用时间
data[‘creatDate’] - data[‘regDate’]，反应汽车使用时间，一般来说价格与使用时间成反比

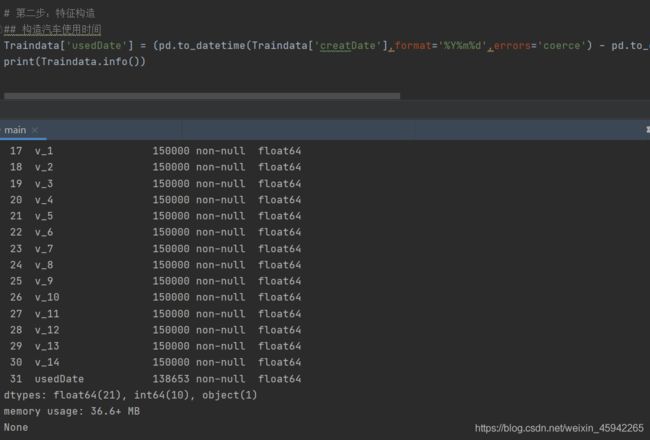
新构造的特征非空值有138653个
新构造的特征有空值11347个

我们可以选择删除，也可以选择放着。
但是这里不建议删除，因为删除缺失数据占总样本量过大，7.5%
我们可以先放着，因为如果我们 XGBoost 之类的决策树，其本身就能处理缺失值，所以可以不用管；

第三步：数据分桶

数据分桶，把数据分段离散化，相当于放在一个个桶里。

以 power 为例，时候我们的缺失值也进桶了。
为什么要做数据分桶呢，原因有很多：
1.离散后稀疏向量内积乘法运算速度更快，计算结果也方便存储，容易扩展；
2.离散后的特征对异常值更具鲁棒性，如 age>30 为 1 否则为 0，对于年龄为 200 的也不会对模型造成很大的干扰；
3.LR 属于广义线性模型，表达能力有限，经过离散化后，每个变量有单独的权重，这相当于引入了非线性，能够提升模型的表达能力，加大拟合；
4.特征离散后模型更稳定，如用户年龄区间，不会因为用户年龄长了一岁就变化
5.离散后特征可以进行特征交叉，提升表达能力，由 M+N 个变量编程 M*N 个变量，进一步引入非线形，提升了表达能力；
当然还有很多原因，LightGBM 在改进 XGBoost 时就增加了数据分桶，增强了模型的泛化性。

常用的有等频分桶，等距分桶。
分桶可以用pandas.cut()函数，根据指定分界点对连续数据进行分箱处理
pd.cut 可以指定区间将数字进行划分，以下三个值将数据划分成两个区间（及格或者不及格）：
其中的labels值得注意一下，有三种取值，默认是none,返回的区间，bool值，如果是false，则返回索引，即如果分成30个桶，则返回0，1,2,3，这样的区间对应的桶的序号，还可以是数组，为每一个区间命名，方便理解，比如给每个分数段的分数命名为A,B,C,D等(参考文档)

默认返回的是区间分桶，分成了30个筒，如第一个桶装的是（0，10】区间的数，第二个筒是（10：20】。。。。共30个筒。

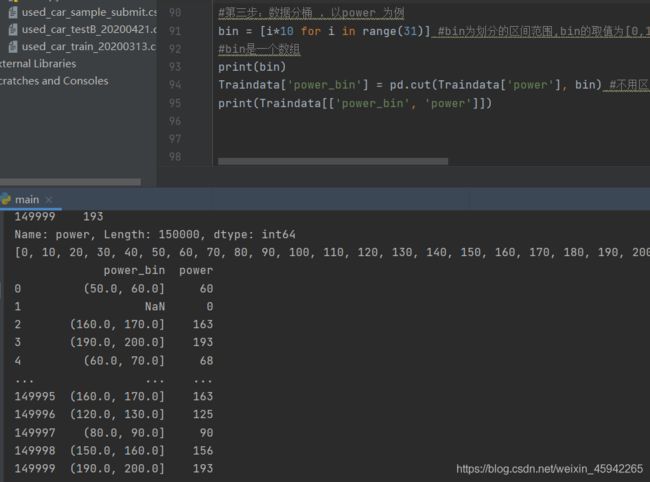
当标签=false时，返回的是筒子的索引号。如第一个筒子索引号为0，第二个为1.。

数据分桶详解

一般在建立分类模型时，需要对连续变量离散化，特征离散化后，模型会更稳定，降低了模型过拟合的风险。比如在建立申请评分卡模型时用logistic作为基模型就需要对连续变量进行离散化，离散化通常采用分桶法。

数据分桶是一种数据预处理技术，用于减少次要观察误差的影响，是一种将多个连续值分组为较少数量的“桶”的方法。
例如，例如我们有一组关于人年龄的数据，如下图所示：

现在我们希望将他们的年龄分组到更少的间隔中，可以通过设置一些条件来实现：

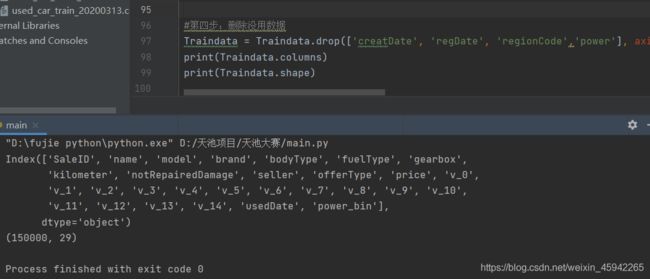
删除不需要的数据

把之前用来构造新特征的数据可以删除掉。以及没用的也可以删除掉。
此时新构造的加上删除没用的，共29列特征。

特征归一化

这一步主要是针对会涉及距离计算的模型如线性回归，SVM等，如果入模的特征在量纲上不相等，在计算距离时量纲大的特征会决定模型的结果。

总结——特征

特征工程主要涉及数据的处理、特征的构造和特征筛选。

1.特征构造：

我们可以看到bodyType、 fuelType等为取几个值的离散变量。可以看到这几个变量的值，只是代表类别，并不代表实际的大小，根据值大小的分裂并不能代表实际的意义。所以我们准备把每一个类别切分出来，形成非0即1的二分变量。

当我们采用基于树模型（XGBoost，LightGBM)来解决回归问题时，针对每一棵树，需要做的是确定分裂的变量，以及分裂点。

这些属性值种，还包含着NAN的类别（如bodytype类别有0，1，2，3，4，5，6，7，nan，共9种不同的取值/九种类别）

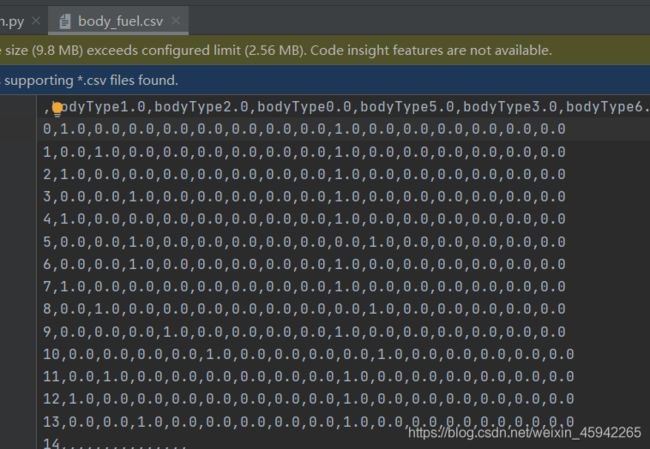
这里将nan类别填充为-1,获得除nan外的所有属性值列表,将bodyType和fuelType所有的属性值切分出来，用1和0表示是否属于该属性，并保留nan值。最后将处理后的结果保存为csv文件。

把每一个类别切分出来，形成非0即1的二分变量。

2.异常类型处理

我们在探索数据集时，看到notRepairedDamage列为object类型，也从它的数值分布，看到它实质上为二分类变量，只是数据中出现了缺失值，使得为字符串类型，这里我们把缺失值设为nan，将数据类型转化为整型

3.构造新特征

在探索数据时，看到creatDate为汽车上线日期，regDate为汽车注册日期，我们可以用这两个日期来构造汽车使用时间，这很可能是影响汽车价格的重要变量。

4.特征筛选

在特征构造中，我们引入了很多变量，但并不是所有变量对最终构建回归模型都是有用的。
如果将所有变量都放入模型中，一方面会耗费更多时间，另一方面也达不到很好的效果。所有这里将进行特征筛选。
不必要的特征会降低训练速度、降低模型可解释性，并且最重要的是还会降低其在测试集上的泛化表现。

具体步骤为：先通过相关性分析，删除掉与交易价格相关性很弱的变量（因为构建的许多变量和交易价格都是非常弱的相关，所以先进行这一步可以排除掉大量的变量，这可以减少后面根据模型来做特征帅选的时间），接着再根据 lightGBM模型中的变量重要性来去除掉低重要性的变量。

先根据相关性进行初步筛选

前面EDA总结中分析过了。

根据lightGBM模型进行筛选

我们可以基于树模型的机器学习模型，求取特征重要度，来进行特征筛选。这里选用lightGBM。

5.缺失值处理：

一般处理缺失值的方式为：
删除有缺失值的行
删除有缺失值的列
将缺失值设置为某个值
对于user_time、notRepairedDamage_new两列的缺失值比例较大，删除有缺失值的行将会损失掉比较多的数据。
所以这里，采用将缺失值设置为某个值的方法。
我在这里把缺失值设置为均值数。

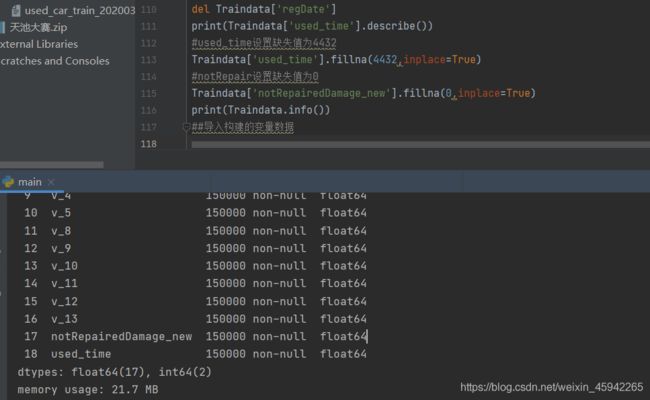
总结——模型选择

首先，我们先训练一个线性模型，来对数据进行初探：

为了评判模型的拟合优度，这里先定义一计算模型拟合效果的指标（包括MAR、MSE、RMSE)函数：
除了模型的拟合效果外，模型的泛化能力也是评判模型的重要指标，甚至是更重要的指标。我们采用交叉验证的方法来验证模型的泛化能力，这里也先定义一个模型泛化能力的指标计算函数:

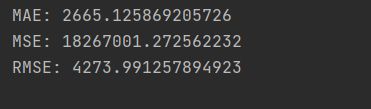
可以看到MAE的值很大，说明线性回归不是一个好模型。

试用随机森林：
MAE有了非常大的改进，但是该模性可能存在过拟合，我们来利用10折交叉验证来验证模型的泛化性能，这里我们采用负的MAE作为得分：

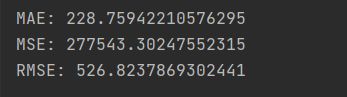
10次平均的MAE为655，虽然比构造的模型MAE大，但其值较小，是一个不错的模型。为了选择好的模型，我们进一步构建GBDT、XGBoost和LightGBM模型。
GBDT：

GBDT整体上不如随机森林模型，但是GBDT模型的10次交叉验证的平均MAE得分和模型的MAE很相近，模型的泛化能力较强。

XGBoost：

XGBoost模型整体好于GBDT 模型，并且泛化能力也很好。XGBoost是对GBDT的改进，其性能一般较GBDT更优，

LightGBM：

总结——模型调优

在模型选择部分，我们对比了不同的模型，发现随机森林、XGBoost和LightGBM三个模型较优，因此我们选择这几个模型来构建预测模型，并进一步进行模型调优，也就是超参数选择。

超参数调整的方法优很多，有手动，有自动。这里我们采用自动调参的方法，
自动调参法在一般有网格搜索、随机搜索和贝叶斯方法。
网格搜索是对所以的参数空间进行搜索，速度一般很慢，但能得到参数空间中的最优参数。
随机搜索速度较快，但可能会错过最优参数。
贝叶斯方法是利用贝叶斯观点来进行参数调优，具体可以参考Python 环境下的自动化机器学习超参数调优，它可以保证速度的情况下，尽可能搜索到最优超参数组合。由于网格搜索实在是太慢了，这里我采用随机搜索方法和贝叶斯方法两种来进行超参数搜索。

由于网格搜索实在是太慢了，这里我采用随机搜索方法和贝叶斯方法两种来进行超参数搜索。

利用随机搜索对随机森林来进行调优

我们利用sklearn.model_selection模块中的RandomizedSearchCV来进行随机搜索，搜索的超参数包括bootstrap，最大特征数max_features，树的最大深度max_depth，n_estimators。
利用5折交叉验证得分来作为模型优劣的判断标准

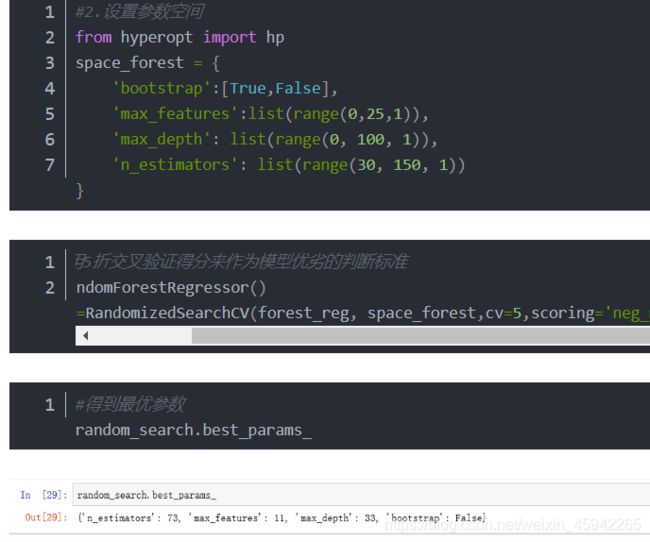
总结——模型融合

模型融合是对调优后的模型的结果进行融合，以提高预测效果。模型融合的方式有：
简单加权融合
stacking/blending
boosting/bagging（在xgboost，Adaboost,GBDT中已经用到）
这里我们采用简单加权融合。

模型融合的结果好于单个模型的效果。接下来，我们可以将上面过程中确定的最优模型和模型的融合方式应用到测试集，完成整个的项目。