第十二届蓝桥杯试题E 最短路径 Python 狄克斯特拉解法 超详细
导语:
距离蓝桥杯比赛还有75天 和小郑一起加油
问题描述:
考察知识点:狄克斯特拉算法+最小公倍数
不妨先看看如何求最小公倍数:
def lcm(a,b):#求最小公倍数
s=a*b
while b:
a,b=b,a%b
return int(s/a)对于自然数a,b 最小公倍数*最大公倍数=ab 因此求出最大公倍数即可 而求最大公倍数可以使用辗转相除法
来到狄克斯特拉算法: 算法用于解决最短带权路径问题 如果你不会使用字典,建议先去掌握一下字典的基本用法再来读下面的文字~
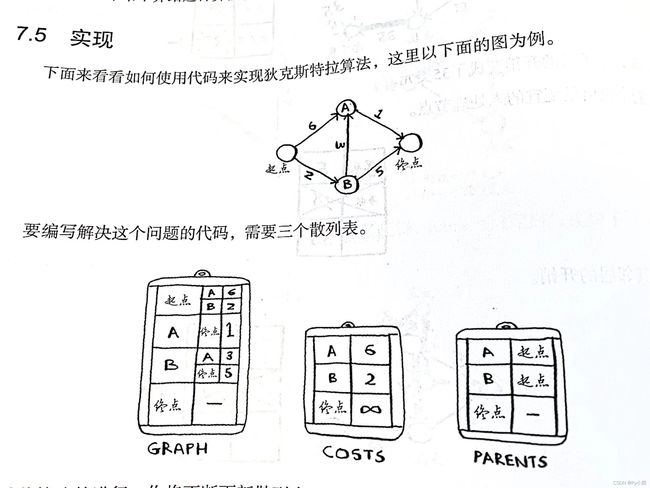
以上面这副图为例子 从起点到终点一共有三种路径
起点>>A>>终点 路径长度6+1=7
起点>>B>>终点 路径长度2+5=7
起点>>B>>A>>终点 路径长度2+3+1=6
显然 最短路径是6 因而 如果我们知道了所有节点的关系 就可把所有的路径长度列出来 取最小即可
但是这样 太过复杂 所以我们引入了狄克斯特拉算法
狄克斯特拉算法包括四个步骤:
(1)找出最便宜的节点P (这么说有点抽象 其实是可以这样想 把连接节点的边 对应的权值比作需要花费的金钱,也就是找出一个花最少的钱能够去的节点)
(2)对于节点P,研究它的邻居,检查是否有前往他们更短的路径,有就更新 (更新除了要更新路径 还要更新父节点,父节点这里不理解没事,后面会在提到)没有就不变
(3)记录这一轮的节点P(作为处理过的节点),对未处理过的节点重复(1)(2),直至所有节点都被处理过
(4)计算最终路径
以上面这幅图为例 我们需要创建字典graph,costs,parent,以及准备一个保存已处理的列表
用途:graph用来保存 每个节点和每个节点邻居以及节点到节点邻居的费用
graph={} graph['start']={'A':6,'B':2} graph['A']={'end':1} graph['B']={'A':3,'end':5} graph['end']={} #结果:{'start': {'A': 6, 'B': 2}, 'A': {'end': 1}, 'B': {'A': 3, 'end': 5}, 'end': {}}
cost用来保存前往某个节点花费的钱(最少),由于我们并不知道前往终点最少要花费多少钱,假设为正无穷
cost={}
cost['A']=6
cost['B']=2
cost['end']=float('inf')#表示无穷大parent用来保存父节点,由于我们并不知道终点的父节点是谁,假设为None(你可能会问 图上不是很明显父节点是A B吗?是的没错,但是你回到前面的四步骤看看,父节点的更新是需要伴随着最短路径的更新,由于我们并不知道前往终点的最短路径,所以暂且假设为None)
parent={}
parent['A']='start'
parent['B']='start'
parent['end']=None下面呈现代码:
graph={}
graph['start']={'A':6,'B':2}
graph['A']={'end':1}
graph['B']={'A':3,'end':5}
graph['end']={}
cost={}
cost['A']=6
cost['B']=2
cost['end']=float('inf')#表示无穷大
parent={}
parent['A']='start'
parent['B']='start'
parent['end']=None
already=[]
def most_cheap(cost):
most_cheap,most_cheap_node=float('inf'),None
for node in cost.keys():
costs=cost[node]
if costs输出结果 符合预期
>>> cost
{'A': 5, 'B': 2, 'end': 6}如果懂了上面这个例题的你再来处理蓝桥杯这道题就不会那么难了
根据题目意思 给出一个数字a 与他连接的数字包括[a+1,a+21] 与上面例题不同在于:邻居变多了
其次题目说是无向边 无向图意味着两个节点彼此指着对方 双向互通 而狄克斯特拉算法只适用于有向无环图 但是 本题依然可以使用狄克斯特拉算法 原因在于 要求最短路径势必每条边至多走一次 如果最短路径中存在有条边走了两次 意味着第二次行走的时候回到了还未走之前的节点 然后继续行走 那完全可以直接不走在一开始!因而每条边最多只能走一次
下面用狄克斯特拉算法解决本题:小郑自己写的 并且答案对了 (标准答案是10266837)
def lcm(a,b):#求最小公倍数
s=a*b
while b:
a,b=b,a%b
return int(s/a)
graph={}
for i in range(1,2021):
graph[i]={}
if i<=2000:
for j in range(i+1,i+22):
graph[i][j]=lcm(i,j)
else:
for j in range(i+1,2022):
graph[i][j]=lcm(i,j)
graph[2021]={}#终点
cost={}
#初始化 start的邻居
for i in graph[1]:
cost[i]=graph[1][i]
#start的邻居之外初始化为无穷大
for i in range(23,2022):
cost[i]=float('inf')
parent={}
#初始化 [2,23]的父节点为1
for i in range(2,24):
parent[i]=1
#余下的父节点初始化为None
for i in range(24,2022):
parent[i]=None
already=[]
def most_cheap(cost):
most_cheap,most_cheap_node=float('inf'),None
for node in cost.keys():
costs=cost[node]
if costs本题具有一定难度 需要反复斟酌 我是小郑 在备战蓝桥杯的路上 希望和你一起加油!
对于本题还有动态规划解法 小郑还没想过 ~不过很快就会再出一篇啦