蒟蒻的ACM数据结构(一)-线段树
浅谈线段树的指针写法
-
- 一、基本概念
- 二、代码实现与基本操作
-
- 0.基础数据结构
- 1.建树 built函数
- 2. 单点查询
- 3.单点修改
- 4.区间查询
- 5.区间修改
- 三.优化
-
- (一). Lazy-Tag懒标记
-
- 思想实现
- 代码实现
-
- 0.核心代码 pushdown
- 1.树本体
- 2.建树
- 3.单点查询和单点修改无改变
- 4.区间查询
- 5.区间修改
- (二). 离散化
- (三).子树收缩
- 数组实现
- 练习题目
欢迎各大佬,大牛对本文指正,也希望本文能对各位有所帮助
%%%
一、基本概念
- 线段树是一棵二叉搜索树,它储存的是一个区间的信息。
- 每个节点以结构体的方式存储,结构体包含以下几个信息:每个节点以结构体的方式存储,结构体包含以下几个信息:
- 区间左端点、右端点
- 区间所代表的值
- 该节点的子节点
每个节点的左孩子区间范围为[left,mid],右孩子为[mid+1,right]
二、代码实现与基本操作
0.基础数据结构
#ifndef NULL //防报错
#define NULL 0
#endif
typedef struct Segment_Tree* Node;
struct Segment_Tree {
int d;
int left, right;
Node lson, rson;
}*root;
1.建树 built函数
Node built(int left, int right)
{
Node p = new(Segment_Tree);//Node p=(Node) malloc(sizeof(Segment_Tree));,c用法
//申请一个新内存,并令p指向该处
p->left = left; //储存区间信息
p->right = right;
if (left == right) {
p->d = a[left]; //scanf("%d",&p->d),cin>>p->d,皆可,及储存数据
p->lson = NULL; //令左儿子和右儿子指向NULL
p->rson = NULL;
}
else {
int mid = (left + right) / 2; //二分
p->lson = built(left, mid); //左儿子
p->rson = built(mid + 1, right); //右儿子
p->d=p->lson->d+p->rson->d; //存储左儿子和右儿子的和
}
return p; //返回指向该处的指针
}
除了建树,相应关闭树的函数为:
void close(Node p)
{
if (p != NULL) {
close(p->lson);
close(p->rson);
delete(p); //free(p);c用法
}
return;
}
非常需要注意的一件事,每次用指针建立树的时候,请务必写一个关闭清理申请的内存的函数
2. 单点查询
(1).查找k位置的数据
int find(Node p, int k)
{
if (p->left == p->right&&p->left == k)
return p->d;
int mid = (p->left + p->right) / 2;
if (k <= mid)
return find(p->lson, k);
return find(p->rson, k);
}
3.单点修改
(1).知道点所在位置,修改该点处值
int update(Node p, int x,int k) //对x位置的值,进行k值的变动
{
if (p->left == p->right&&p->left == x) //如过找到了k位置
return p->d +=k; //对该点值进行操作,可以为+-*/等
int mid = (p->left + p->right) / 2; //判断该点在左区间还是右区间
if (x <= mid) //如果是左区间,只对左区间进行递归查询
return p->d = update(p->lson, x, k)+p->rson->d; //查找完后对父节点存储值进行修改
return p->d = p->lson->d+update(p->rson, x, k); //不是该点,也不在左区间,只能是右区间
}
4.区间查询
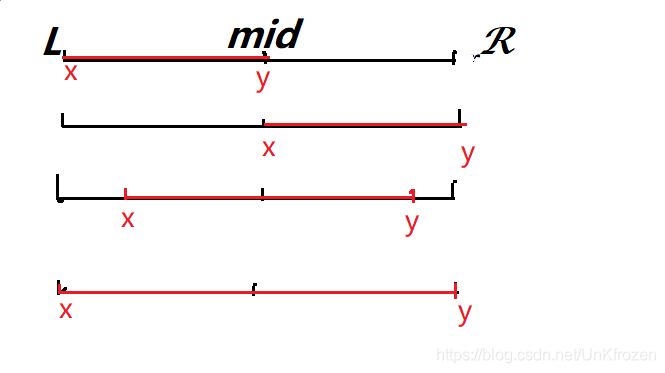
所给区间仅可能为上图四种情况。
通过一定操作,我们都可以将上三种,全部转换为最后一种直接输出。
闲话少说,代码实现
int find(Node p, int x,int y) //注,这里假设任意x,y,都有x
{
if (p->left == x && p->right == y) //如果是第四种情况,直接返回
return p->d;
int mid = (p->left + p->right) / 2; //求中间值
if (y <= mid) //如果查询区间在mid左边,因为x
return find(p->lson, x, y); //那么直接递归左儿子
if (x > mid) //如果查询区间在mid右边,因为mid
return find(p->rson, x, y); //那么直接递归右儿子
return find(p->lson, x, mid)+find(p->rson, mid + 1, y); //两式都不符合,及x<=mid
//则从mid为中间值分开
//左儿子查询[x,mid],右儿子查询[mid+1,y]
}
5.区间修改
int update(Node p, int x, int y, int k) //设区间为[x,y],修改的值为k
{
if (p->left == p->right && p->left == x) //如果是这个区间内的元素,就让它+k
return p->d+=k;
int mid = (p->left + p->right) / 2; //二分
if (y <= mid) //如果区间在中值的左侧
return p->d=update(p->lson, x, y,k)+p->rson->d; //仅需更新左儿子的值,并更新父亲的值
if (x > mid) //如果区间在中值的左侧
return p->d=p->lson->d+update(p->rson, x, y,k); //同上
return p->d=update(p->lson, x, mid,k) + update(p->rson, mid + 1, y,k); //如果区间被中值分开
}
三.优化
(一). Lazy-Tag懒标记
我们考虑一下区间改值的过程:当更改某个区间的值的时候,子区间也跟着更改。显然,在大数据下,这样操作会导致TLE。
怎么办?
这时我们就引入一个优化方法,叫做Lazy-Tag懒标记。
何为懒标记呢?顾名思义,就是用来偷懒的减少修改时消耗时间的。即:
当我想要对某一区间的所有元素都+k时,在修改该区间节点时,对其打上标记lazy,并记lazy为k,修改该节点的值为+区间长度*k,立刻return,而不将该节点下面的所有子节点一一修改。
思想实现
如图示:1~4的值分别为1,2,3,4

我们选择对[1,2]区间进行修改,要求改区间所有值+2,则:在区间[1,2],打上标记lazy=2,并修改其值为3+(2-1+1)*2,直接返回,并不对其子节点进行修改

当我们再次对[1,2]区间修改时,并要求区间内所有的值+1,则:由于[1,2]有标记lazy=2,于是我们将lazy标记向其子节点传导,并修改其子节点的值。再在[1,2]区间打上lazy=1,修改值为(2-1+1)*1,返回。

代码实现
0.核心代码 pushdown
void pushdown(Node p)
{
if (p->lson != NULL) { //如果该节点还有后续节点
p->lson->lazy += p->lazy; //令子节点lazy继承父节点lazy,下同
p->lson->d += (p->lson->right - p->lson->left + 1)*p->lazy; //修改子节点的值,下同
p->rson->lazy += p->lazy;
p->rson->d += (p->rson->right - p->rson->left + 1)*p->lazy;
}
p->lazy = 0; //令该节点的lazy清零
}
1.树本体
#ifndef NULL
#define NULL 0
#endif
typedef struct Segment_Tree* Node;
struct Segment_Tree {
int d,lazy; //仅仅多了一个lazy标记
int left, right;
Node lson, rson;
}*root;
2.建树
Node built(int left, int right)
{
Node p = new(Segment_Tree);
p->left = left;
p->right = right;
p->lazy = 0; //只是对lazy标记进行初始化
if (left == right) {
p->d = a[left];
p->lson = NULL;
p->rson = NULL;
}
else {
int mid = (left + right) / 2;
p->lson = built(left, mid);
p->rson = built(mid + 1, right);
p->d = p->lson->d+p->rson->d;
}
return p;
}
void close(Node p)
{
if (p != NULL) {
close(p->lson);
close(p->rson);
delete(p); //free(p);c用法
}
return;
}
3.单点查询和单点修改无改变
4.区间查询
long long find(Node p, int x, int y) //区间查询
{
if (p->lazy != 0) //解决一下历史遗留问题再查询
pushdown(p);
if (p->left == x && p->right == y) //其他未变
return p->d;
int mid = (p->left + p->right) / 2;
if (y <= mid)
return find(p->lson, x, y);
if (x > mid)
return find(p->rson, x, y);
return find(p->lson, x, mid)+find(p->rson, mid + 1, y);
}
5.区间修改
int update(Node p, int x, int y, int k) //区间修改
{
if (p->lazy!=0) //如果该节点的lazy不为零,就处理一下
pushdown(p);
if (p->left == x && p->right==y) { //如果是要进行修改的节点,便让该节点的lazy为k,并修改值
p->lazy = k;
return p->d += k*(y - x + 1);
}
int mid = (p->left + p->right) / 2;
if (y <= mid)
return p->d = p->rson->d+update(p->lson, x, y, k);
if (x > mid)
return p->d = p->lson->d+ update(p->rson, x, y, k);
return p->d = update(p->lson, x, mid, k) + update(p->rson, mid + 1, y, k);
}
(二). 离散化
蒟蒻还没学会嘤嘤嘤
所谓离散化就是将无限的个体映射到有限的个体中,从而提高算法效率。
举个简单的例子,一个实数数组,我想很快的得到某个数在整个数组里是第几大的,并且询问数很多,不允许每次都遍历数组进行比较。
那么,最直观的想法就是对原数组先进行一个排序,询问的时候只需要通过二分查找就能在O( log(n))的时间内得出这个数是第几大的了,离散化就是做了这一步映射。 对于一个数组[1.6, 7.8, 5.5, 11.1111,99999, 5.5],离散化就是将原来的实数映射成整数(下标),如图所示:
这样就可以将原来的实数保存在一个有序数组中,询问第K大的是什么称为正查,可以利用下标索引在O(1)的时间内得到答案;询问某个数是第几大的称为反查,可以利用二分查找或者Hash得到答案,复杂度取决于具体算法,一般为O(log(n))。
--------------------- 作者:英雄哪里出来
来源:CSDN 原文:https://blog.csdn.net/WhereIsHeroFrom/article/details/78969718
版权声明:本文为博主原创文章,转载请附上博文链接!
(三).子树收缩
蒟蒻还没学会嘤嘤嘤
子树收缩是子树继承的逆过程,子树继承是为了两棵子树获得父结点的信息;而子树收缩则是在回溯的时候,如果两棵子树拥有相同数据的时候在将数据传递给父结点,子树的数据清空,这样下次在访问的时候就可以减少访问的结点数。
--------------------- 作者:英雄哪里出来
来源:CSDN 原文:https://blog.csdn.net/WhereIsHeroFrom/article/details/78969718
数组实现
#include练习题目
洛谷P2251
裸的RMQ问题,数据量小.
洛谷P3372
洛谷P3373
洛谷线段树模板题
