数据结构----线段树(区间树)

1. 概述

1. 解决的问题：

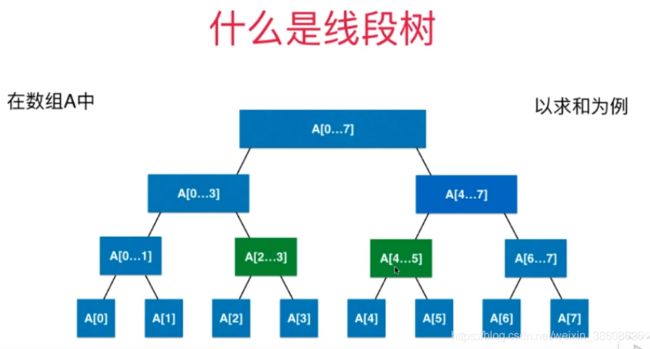
   1. 主要解决“区间”相关操作的问题。对区间的数据，需要进行更新和查询操作。
   2. 对于给定的区间。
   3. 更新：更新区间中一个元素或者一个区间的元素。
   4. 查询：查询一个区间的最大值、最小值或者区间数字和。

2. 解决方式：

   1. 数组：通过索引可以进行进行区间操作；但是，更新和查询的时间复杂度都是O(n)，性能较低。
   2. 线段树：更新和查询的时间复杂度都是O(log n)，性能较高。

3. 线段树形式
   

4. 线段树规则

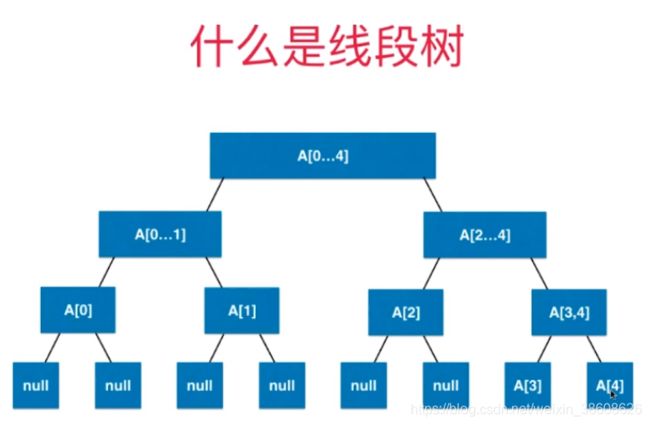
   1. 线段树不是完全二叉树，是平衡二叉树(树的最高层数和最低层数，相差为1)。

5. 使用数组构建线段树

   1. 需要多少个节点，才能构建成线段树？
      1. 按照满二叉树算，若n=2^k，则需要2N的空间。
      2. 最坏情况，若n=2^k+1，则需要4N的空间。
      3. 图示
         

2. 源码

/**
 * 线段树操作接口
 */
public interface Merger<T> {
    // 对线段树的具体操作, 由用户指定.
    T merge(T a, T b);
}


/**
 * 线段树
 */
public class SegmentTree<T> {
    private T[] data;
    private T[] tree;
    private Merger<T> merger;

    public SegmentTree(T[] source, Merger<T> merger) {        
    	this.merger = merger;

        data = (T[]) new Object[source.length];
        System.arraycopy(source, 0, data, 0, source.length);

        // 数组存储在线段树中需要(4 * n)个空间.
        tree = (T[]) new Object[4 * source.length];
        buildSegmentTree(0, 0, data.length - 1);
    }
    
    /**
     * 在treeIndex位置创建表示区间[l...r]的线段树.
     *
     * @param treeIndex
     * @param left:     左边界
     * @param right：有边界
     */
    private void buildSegmentTree(int treeIndex, int left, int right) {        
    	if (left == right) {
            tree[treeIndex] = data[left];
            return;
        }
        
        int leftChild = leftChild(treeIndex);
        int rightChild = rightChild(treeIndex);

        // 这样进行加法, 可以有效保证整型溢出.
        // mid = 小 + ((大 - 小) / 2)
        int mid = left + (right - left) / 2;

        // 构建左子树[left...mid]
        buildSegmentTree(leftChild, left, mid);

        // 构建右子树[mid + 1...right]
        buildSegmentTree(rightChild, mid + 1, right);

        // 通过暴露Merger接口, 提供给用户自己定制操作.
        tree[treeIndex] = merger.merge(tree[leftChild], tree[rightChild]);
    }
    
    public int getSize() {
        return data.length;
    }
    
    public T get(int index) {
        if (index < 0 || index >= data.length) {
            throw new IllegalArgumentException("Index is not exist!");
        }
        
        return data[index];
    }
    
    public T query(int queryLeft, int queryRight) {
        if (queryLeft < 0 || queryRight < 0 || queryLeft >= data.length 
        	|| queryRight >= data.length || queryLeft > queryRight) {
            throw new IllegalArgumentException("Index is not exist!");
        }
        
        return query()
    }

    /**
	 * 在treeIndex为根的线段树中[left...right]的范围中,
	 * 搜索[queryLeft, queryRight]区间内的值.
	 *
	 * @return : 查询的返回值.
	 */
    private T query(int treeIndex, int left, int right, int queryLeft, int queryRight) {
	    if (left == queryLeft && right == queryRight) {
	        return tree[treeIndex];
	    }
	
	    int mid = left + (right - left) / 2;
	    int leftChild = leftChild(treeIndex);
	    int rightChild = rightChild(treeIndex);
	
	    if (queryLeft >= mid + 1) {
	        return query(rightChild, mid + 1, right, queryLeft, queryRight);
	    } else if (queryRight <= mid) {
	        return query(leftChild, left, mid, queryLeft, queryRight);
	    }
	
	    T leftResult = query(leftChild, left, mid, queryLeft, mid);
	    T rightResult = query(rightChild, mid + 1, right, mid + 1, queryRight);
	    return merger.merge(leftResult, rightResult);
	}

	// 更新index位置的值.
	public T set(int index, T element) {
		if (index < 0 || index >= data.length) {
			throw new IllegalArgumentException("Index isn't exist!");
		}
		
		T oldData = data[index];
		data[index] = element;
		set(0, 0, data.length - 1, index, element);
		return oldData;
		}
	
	private void set(int treeIndex, int left, int right, int index, T element) {
		if (left == right) {
		System.out.println("OLD: " + tree[treeIndex]);
		tree[treeIndex] = element;
		return;
		}
		
		int mid = left + (right - left) / 2;
		int leftChild = leftChild(treeIndex);
		int rightChild = rightChild(treeIndex);
		
		if (index >= mid + 1) { // 肯定在右子树
		set(rightChild, mid + 1, right, index, element);
		} else { // 肯定在左子树
		set(leftChild, left, mid, index, element);
		}
		
		// 更新完成节点数据, 相应的父节点的数据也需要更新.
		tree[treeIndex] = merger.merge(tree[leftChild], tree[rightChild]);
	}

    /**
     * 返回父节点对应的左孩子节点索引.
     *
     * @param parentIndex: 父节点索引.
     * @return : 左孩子节点索引.
     */
    private int leftChild(int parentIndex) {        
    	return parentIndex * 2 + 1;
    }
    
    /**
     * 返回父节点对应的右孩子节点索引.
     *
     * @param parentIndex: 父节点索引.
     * @return : 右孩子节点索引.
     */
    private int rightChild(int parentIndex) {        
    	return parentIndex * 2 + 2;
    }
    
    @Override
    public String toString() {        
    	StringBuilder result = new StringBuilder();
        result.append("[");
        for (int i = 0; i < tree.length; i++) {            
        	if (tree[i] != null) {
                result.append(tree[i]);
            } else {                
            	result.append("Null");
            }
            
            if (i != tree.length - 1) {
                result.append("->");
            }        
		}

        result.append("]");
        return result.toString();
    }
    
    public static void main(String[] args) {
        Integer[] nums = {-2, 0, 3, -5, 2, -1};
        // 第二个参数，决定了线段树的功能是求和、最大值、最小值等等。
        SegmentTree<Integer> tree = new SegmentTree<>(nums, (a, b) -> a + b);
        System.out.println(tree);
    }
}