递归专项-数据结构-线段树
线段树
比如我们有一个大小为6的数组,其索引为0,1,2,3,4,5,那么我们就可以构建出如下的一颗线段树,下图所示:
考虑到一棵完全二叉树,假设右k层,则其总数为2^0 + 2 ^1 +… + 2 ^k
= 2^(k + 1) - 1,
所以针对一棵线段树,其最好情况下是一棵满二叉树,这时候线段是的大小为2 * n即可,但是往往由于数据因素可能会变成一课完全二叉树,而不是恰好就是满二叉树,这时候如果需要涵盖所有的数据,就需要开辟2 * (2 * n) 才行【即多开一层空间】
所以根据上面的阐述,假设我们有一个数组data[n], 那么开辟的tree数组大小就是4n。构造函数如下:
private E[] tree;
private E[] data;
private Merger merger;
public SegmentTree(E[] value, Merger merger) {
this.data = (E[])new Object[value.length];
for (int i = 0; i < value.length; i++) {
data[i] = value[i];
}
this.tree = (E[])new Object[4 * value.length];
this.merger = merger;
buildSegmentTree(0,0,this.data.length - 1);
}
首先我们可以通过递归方式插入数据:针对每一个区间,都为分裂成两个区块,直到不可分裂为止(递归终止条件是单独的index成为区块)
/**
*
* @param index: 该段的索引
* @param left: 线段树的左段,对应data 里面的索引
* @param right: 线段树的右段,对应data 里面的索引
* @return: 该段存储的值
*/
public E buildSegmentTree(int index, int left, int right) {
if (left == right) {
tree[index] = data[left];
return tree[index];
}
int mid = left + (right-left) / 2;
// 分裂成2个段
// 左段
E leftValue = buildSegmentTree(2 * index + 1, left, mid);
// 右段
E rightValue =buildSegmentTree(2 * index + 2, mid + 1, right);
// 聚合左段和右段的值
tree[index] = this.merger.merge(leftValue, rightValue);
return tree[index];
}
根据区间查询结果值:本质上还是查query的范围对应线段树的哪些区间组合。
public E queryByRange(int index, int treeL, int treeR, int left, int right) {
if (left == treeL && right == treeR) {
return tree[index];
}
int mid = treeL + (treeR - treeL) / 2;
if (right <= mid) {
return queryByRange(2 * index + 1, treeL, mid, left, right);
}
if (left >= mid + 1) {
return queryByRange(2 * index + 2, mid + 1, treeR, left, right);
}
// 即在左边又在右边
return merger.merge(queryByRange(2 * index + 1, treeL, mid, left, mid) , queryByRange(2 * index + 2,mid + 1, treeR, mid + 1, right));
}
更新原始数组索引的值:
public void update(int index, E e) {
updateDg(0, 0, data.length - 1, index , e);
}
private void updateDg(int treeIndex, int l, int r, int dataIndex, E e) {
if (l == r) {
tree[treeIndex] = e;
return;
}
int mid = l + (r - l) / 2;
if (dataIndex > mid) {
updateDg(2 * treeIndex + 2, mid + 1, r, dataIndex, e);
} else {
updateDg(2 * treeIndex + 1, l, mid, dataIndex, e);
}
tree[treeIndex] = merger.merge(tree[2 * treeIndex + 1], tree[2 * treeIndex + 2]);
}
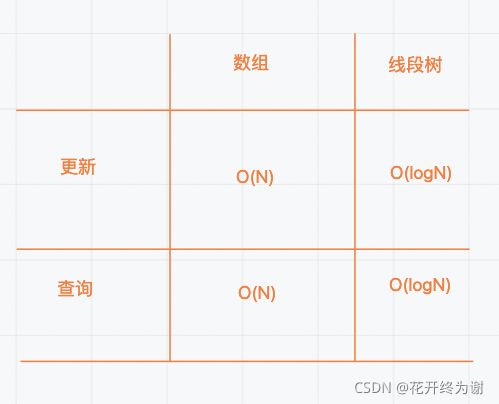
线段树比较适合针对一批数组,需要频繁得出查询范围区间的值得情况。其与数组之间的对比如下:
其完整代码如下:
package data.structure.segmenttree;
import com.google.common.base.Preconditions;
public class SegmentTree {
private E[] tree;
private E[] data;
private Merger merger;
public SegmentTree(E[] value, Merger merger) {
this.data = (E[])new Object[value.length];
for (int i = 0; i < value.length; i++) {
data[i] = value[i];
}
this.tree = (E[])new Object[4 * value.length];
this.merger = merger;
buildSegmentTree(0,0,this.data.length - 1);
}
public int getSize() {
return data.length;
}
public E get(int index) {
Preconditions.checkArgument(index >= 0 && index < data.length, "index not valid");
return data[index];
}
/**
*
* @param index: 该段的索引
* @param left: 线段树的左段,对应data 里面的索引
* @param right: 线段树的右段,对应data 里面的索引
* @return: 该段存储的值
*/
public E buildSegmentTree(int index, int left, int right) {
if (left == right) {
tree[index] = data[left];
return tree[index];
}
int mid = left + (right-left) / 2;
// 分裂成2个段
// 左段
E leftValue = buildSegmentTree(2 * index + 1, left, mid);
// 右段
E rightValue =buildSegmentTree(2 * index + 2, mid + 1, right);
// 聚合左段和右段的值
tree[index] = this.merger.merge(leftValue, rightValue);
return tree[index];
}
public E queryByRange(int index, int treeL, int treeR, int left, int right) {
if (left == treeL && right == treeR) {
return tree[index];
}
int mid = treeL + (treeR - treeL) / 2;
if (right <= mid) {
return queryByRange(2 * index + 1, treeL, mid, left, right);
}
if (left >= mid + 1) {
return queryByRange(2 * index + 2, mid + 1, treeR, left, right);
}
// 即在左边又在右边
return merger.merge(queryByRange(2 * index + 1, treeL, mid, left, mid) , queryByRange(2 * index + 2,mid + 1, treeR, mid + 1, right));
}
public void update(int index, E e) {
updateDg(0, 0, data.length - 1, index , e);
}
private void updateDg(int treeIndex, int l, int r, int dataIndex, E e) {
if (l == r) {
tree[treeIndex] = e;
return;
}
int mid = l + (r - l) / 2;
if (dataIndex > mid) {
updateDg(2 * treeIndex + 2, mid + 1, r, dataIndex, e);
} else {
updateDg(2 * treeIndex + 1, l, mid, dataIndex, e);
}
tree[treeIndex] = merger.merge(tree[2 * treeIndex + 1], tree[2 * treeIndex + 2]);
}
public void display(int index) {
if (index > tree.length - 1) {
return;
}
System.out.println(tree[index]);
display(2 * index + 1);
display(2 * index + 2);
}
public static void main(String[] args) {
SegmentTree segmentTree = new SegmentTree<>(new Integer[]{1,2,3,4,5}, Integer::sum);
segmentTree.display(0);
Integer integer = segmentTree.queryByRange(0, 0, segmentTree.getSize() - 1, 1, 3);
System.out.println("range 1:3 sum = " + integer);
segmentTree.update(2, 10);
integer = segmentTree.queryByRange(0, 0, segmentTree.getSize() - 1, 1, 3);
System.out.println("range 1:3 sum = " + integer);
}
}