scikit-learn-分类模型评价标准

0 模型指标

---

  本篇博客记录主要的模型评价标准的含义和用法。先看一个我常用的评价指标图（二分类）：

---

1 TP ，FP ，TN ，FN

---

TP：实际正例；预测正例；
FP：实际反例；预测正例；
TN：实际反例；预测反例；
FN；实际正例；预测反例；

---

2 Recall ，Precision ，FPR ， Specificity ，F1-score ，MCC

---

Recall (True Postive Rate):
$$\mathbf{r}\mathbf{e}\mathbf{c}\mathbf{a}\mathbf{l}\mathbf{l}=\mathbf{s}\mathbf{e}\mathbf{n}\mathbf{s}\mathbf{i}\mathbf{t}\mathbf{i}\mathbf{v}\mathbf{i}\mathbf{t}\mathbf{y}=\mathbf{T}\mathbf{P}\mathbf{R}=\frac{\mathbf{T}\mathbf{P}}{(\mathbf{T}\mathbf{P}+\mathbf{F}\mathbf{N})}\text{\hspace{1em}(1)}$$
称呼：查全率/召回率/真正类率
含义：实际为正例中，被预测为正例的比例。

Precision:
$$\mathbf{p}\mathbf{r}\mathbf{e}\mathbf{c}\mathbf{i}\mathbf{s}\mathbf{i}\mathbf{o}\mathbf{n}=\frac{\mathbf{T}\mathbf{P}}{(\mathbf{T}\mathbf{P}+\mathbf{F}\mathbf{P})}\text{\hspace{1em}(2)}$$
称呼：精确率
含义：预测为正例中，实际也为正例的比例。

FPR (False Postive Rate):
$$\mathbf{F}\mathbf{P}\mathbf{R}=\frac{\mathbf{F}\mathbf{P}}{(\mathbf{F}\mathbf{P}+\mathbf{T}\mathbf{N})}\text{\hspace{1em}(3)}$$
称呼：负正类率
含义：实际为负例中，被预测为正例的负例的比例。

TNR (True Negative Rate):
$$\mathbf{S}\mathbf{p}\mathbf{e}\mathbf{c}\mathbf{i}\mathbf{f}\mathbf{i}\mathbf{c}\mathbf{i}\mathbf{t}\mathbf{y}=\mathbf{T}\mathbf{N}\mathbf{R}=\frac{\mathbf{T}\mathbf{N}}{(\mathbf{F}\mathbf{P}+\mathbf{T}\mathbf{N})}\text{\hspace{1em}(4)}$$
称呼：真负类率
含义：实际为负例中，被预测为负例的比例。

F1-score:
$${\mathbf{F}}_1\mathbf{s}\mathbf{c}\mathbf{o}\mathbf{r}\mathbf{e}=\frac{2\ast \mathbf{r}\mathbf{e}\mathbf{c}\mathbf{a}\mathbf{l}\mathbf{l}\ast \mathbf{p}\mathbf{r}\mathbf{e}\mathbf{c}\mathbf{i}\mathbf{s}\mathbf{i}\mathbf{o}\mathbf{n}}{\mathbf{r}\mathbf{e}\mathbf{c}\mathbf{a}\mathbf{l}\mathbf{l}+\mathbf{p}\mathbf{r}\mathbf{e}\mathbf{c}\mathbf{i}\mathbf{s}\mathbf{i}\mathbf{o}\mathbf{n}}\text{\hspace{1em}(5)}$$
称呼：F1-score
含义：是一个兼顾考虑了Precision 和 Recall 的评估指标。通常， F-measure 就是指 Precision 和 Recall 的调和平均数（Harmonic mean）

MCC（Matthews correlation coefficient）:
$$\mathbf{M}\mathbf{C}\mathbf{C}=\frac{(\mathbf{T}\mathbf{P}\ast \mathbf{T}\mathbf{N}-\mathbf{F}\mathbf{P}\ast \mathbf{F}\mathbf{N})}{\sqrt{((\mathbf{T}\mathbf{P}+\mathbf{F}\mathbf{P})\ast (\mathbf{T}\mathbf{P}+\mathbf{F}\mathbf{N})\ast (\mathbf{T}\mathbf{N}+\mathbf{F}\mathbf{P})\ast (\mathbf{T}\mathbf{N}+\mathbf{F}\mathbf{N}))}}\text{\hspace{1em}(6)}$$
称呼：马修斯相关系数
含义：MCC本质上是一个描述实际分类与预测分类之间的相关系数，它的取值范围为[-1,1]，取值为1时表示对受试对象的完美预测，取值为0时表示预测的结果还不如随机预测的结果，-1是指预测分类和实际分类完全不一致。

---

3 macro avg ，micro avg ，weighted avg

---

  这里我们以precision，recall为例进行分析。
  我们首先清楚一点是，我们在计算recall或者precision的时候,是根据某一类别进行计算的，什么意思呢？比如：我们做二分类，0代表正例，1代表反例。根据这样的定义我们可以计算出 TP FP TN FN 以及precision 和recall 。反过来，我们以1 代表正例，0代表反例，同样可以计算出刚才那一堆。这里的avg 嗯就是对刚才的那一堆进行avg。首先我们来看 macro avg。
  macro avg的意思是宏平均，从字面意思我们应该明白大概了。就是对类1的recall值和类0的recall值进行平均，权重是0.5.这个明白了，weighted avg 也差不多啦，weighted avg就是用样本的比例充当权重来计算的。macro avg公式如下
$$\mathbf{r}\mathbf{e}\mathbf{c}\mathbf{a}\mathbf{l}\mathbf{l}=\frac{\mathbf{r}\mathbf{e}\mathbf{c}\mathbf{a}\mathbf{l}{\mathbf{l}}_1+\mathbf{r}\mathbf{e}\mathbf{c}\mathbf{a}\mathbf{l}{\mathbf{l}}_2}{2}\text{\hspace{1em}(7)}$$
我们再来看micro avg公式：
$$\mathbf{r}\mathbf{e}\mathbf{c}\mathbf{a}\mathbf{l}\mathbf{l}=\frac{\mathbf{T}{\mathbf{P}}_1+\mathbf{T}{\mathbf{P}}_2}{(\mathbf{T}{\mathbf{P}}_1+\mathbf{F}{\mathbf{N}}_1+\mathbf{T}{\mathbf{P}}_2+\mathbf{F}{\mathbf{N}}_2)}\text{\hspace{1em}(8)}$$
从公式也可以看出微平均和宏平均的计算层面不一样。precision和recall类似这里就不多说了。
另外，还有就是 f1-score 的宏平均和微平均
macro avg：
$$\mathbf{m}\mathbf{a}\mathbf{c}\mathbf{r}{\mathbf{o}}_{\mathbf{f}}=\frac{\mathbf{f}1+\mathbf{f}2}{2}\text{\hspace{1em}(9)}$$
micro avg：
$$\mathbf{m}\mathbf{i}\mathbf{c}\mathbf{r}{\mathbf{o}}_{\mathbf{f}}=\frac{2\ast \mathbf{m}\mathbf{i}\mathbf{c}\mathbf{r}{\mathbf{o}}_{\mathbf{p}}\ast \mathbf{m}\mathbf{i}\mathbf{c}\mathbf{r}{\mathbf{o}}_{\mathbf{r}}}{\mathbf{m}\mathbf{i}\mathbf{c}\mathbf{r}{\mathbf{o}}_{\mathbf{p}}+\mathbf{m}\mathbf{i}\mathbf{c}\mathbf{r}{\mathbf{o}}_{\mathbf{r}}}\text{\hspace{1em}(10)}$$

---

4 ROC曲线和AUC

---

FPR和TPR
FPR（False Positive Rate）和TPR（True Positive Rate）分别对应着ROC曲线的横纵坐标，其定义如下 ：
$$\mathbf{T}\mathbf{P}\mathbf{R}=\frac{\mathbf{T}\mathbf{P}}{(\mathbf{T}\mathbf{P}+\mathbf{F}\mathbf{N})}\text{\hspace{1em}(11)}$$
$$\mathbf{F}\mathbf{P}\mathbf{R}=\frac{\mathbf{F}\mathbf{P}}{(\mathbf{F}\mathbf{P}+\mathbf{T}\mathbf{N})}\text{\hspace{1em}(12)}$$

对于一个学习器它的预测结果只能产生一对（FPR，TPR），这只能绘制一个点，不足以绘制出一条曲线。实际上对于许多学习器在判定二分类问题时是预测出一个对于真值的范围在[0.0, 1.0]之间的概率值，而判定是否为真值则看该概率值是否大于设定的阈值（Threshold）。例如如果阈值设定为0.5则所有概率值大于0.5的均为正例，其余为反例。因此对于不同的阈值我们可以得到一系列相应的FPR和TPR，从而绘制出ROC曲线。
以下列数据举例：

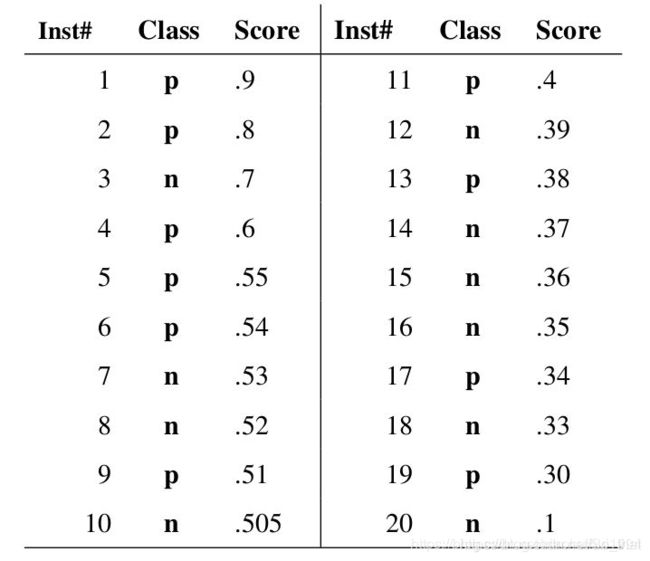
如果我们将他的score值做阈值，也就是说，只有score大于等于0.9时，我们才把样本归类到正样本，这么一来， 在ROC曲线图中，样本1对应的混淆矩阵（confusion matrix）为:

*	预测	*
真实	正例	反例
正例	1	9
反例	0	10

第一个样本score=0.9，所以预测为正样本，其本身也为正样本，其他样本score都<0.9，所以都预测为负样本，从混淆矩阵中，我们可以算出X轴坐标（false positive rate）= 0/（0+10）= 0 和Y轴坐标（true positive rate）= 1/（1+9）= 0.1，所以第一个点为(0,0.1)
依次按照不同的阈值来计算最终得到的图如下：

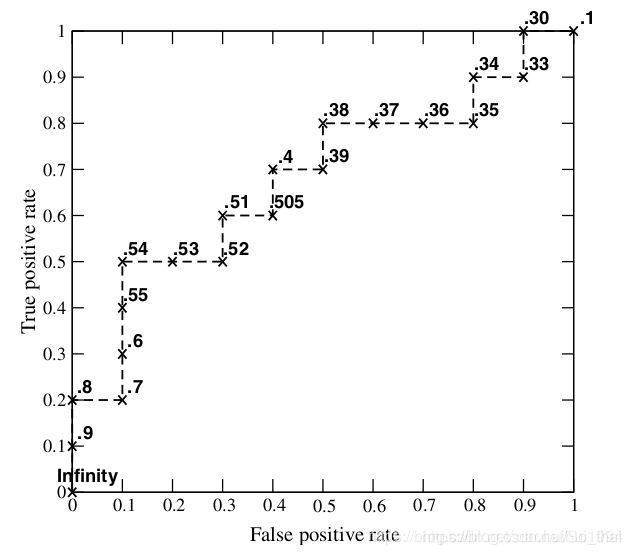
• AUC绘制说明以及图片来源：https://blog.csdn.net/xiaohuihui1994/article/details/87987836

• 关于多分类AUC的原理参看：https://blog.csdn.net/YE1215172385/article/details/79443552

• 同时这里给出一个例子：

from sklearn import datasets
from sklearn import metrics
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import label_binarize
import numpy as np
from xgboost import XGBClassifier
import pandas as pd

iris = datasets.load_iris()
iris_X = iris.data
iris_y = iris.target

y = pd.Categorical(iris_y).codes  # 将标签转换0,1,...
X_train, X_test, y_train, y_test = train_test_split(iris_X, iris_y, test_size=0.3)
y_one_hot = label_binarize(y_test, np.arange(3))

clf=XGBClassifier(random_state=2020)
clf.fit(X_train,y_train)
y_pro=clf.predict_proba(X_test)
y_pre=clf.predict(X_test)

print("AUC:",metrics.roc_auc_score(y_one_hot,y_pro,average='micro'))

#  2、混淆矩阵
metrics.confusion_matrix(y_test, y_pre)

# 4、模型报告
print(metrics.classification_report(y_test, y_pre))

---

5 使用

---

下面是sklearn的部分代码：

 predicted = cross_val_predict(classifier, X, y, cv=cv, n_jobs=cpu_num)
 predict_prob = cross_val_predict(classifier, X, y, cv=cv, n_jobs=cpu_num, method='predict_proba')
 AUC = metrics.roc_auc_score(y, predict_prob[:, 1])
 print("AUC:{}".format(AUC))
 print("ACC:{}".format(metrics.accuracy_score(y, predicted)))
 print("MCC:{}".format(metrics.matthews_corrcoef(y, predicted)))
 print(classification_report(y, predicted, labels=label))
 print("confusion matrix\n")
 print(pd.crosstab(pd.Series(y, name='Actual'), pd.Series(predicted, name='Predicted')))

---

参考

---

https://blog.csdn.net/xiaohuihui1994/article/details/87987836