数据可视化小结
目录
前言
数据分布
箱线图(Box Plot)
直方图(Histogram)
密度图(Density Plot)
小提琴图(Violin Plot)
数据组成
饼图(Pie Chart)
环状图
旭日图
树形图(Tree Map)
华夫饼图(Waffle Chart)
柱状图(Bar Chart)
棒棒糖图(Lollipop Chart)
南丁格尔玫瑰图
堆积柱状图(Stack Bar Chart)
绝对值堆积图
百分比堆积图
堆积面积图(Stack Area Chart)
百分比堆积面积图
分组柱状图(Grouped Bar Chart)
双向柱状图(Bidirectional Bar Chart)
漏斗图(Funnel Chart)
词云(Word Cloud)
地图
热力地图
轨迹地图
数据比较
折线图(Line Chart)
瀑布图(Waterfall Chart)
K线图(Waterfall Chart)
雷达图(Radar Chart)
坡度图(Slope Chart)
桑基图(Sankey diagram)
数据关系
散点图(Scatter Plot)
散点气泡图
相关性热图(Correlogram)
成对比较图(Pairwise Plot)
和弦图(Chord Diagram)
数据可视化之道
前言
俗话说得好,“一图胜千言”,很多时候一组很复杂的数字通过一张图片往往更容易让人理解,甚至还可以更容易使人发现数据之间内在的联系。
对于数据分析,首先要确定分析的是什么类型的数据,离散的?还是连续的?其次数据有什么样的特点,普通的线性数据?还是指数型的?之后就要判断数据随时间的变化、不同数据之间的关系、数据中不同组成部分的占比等。
对于数据展示,则一定要注意确定展示的主题。之后根据主题来设计图表,让数据具有“解释力”,从而讲出自己的“故事”。
数据分布
对于一个连续型数据,首先想要了解这个数据的分布情况,比如成都房价大概在什么区间、平均房价多少等。常常需要一些图表来概览某个数据的分布情况,有时也需要同时展示多个数据的分布进行对比。
箱线图(Box Plot)
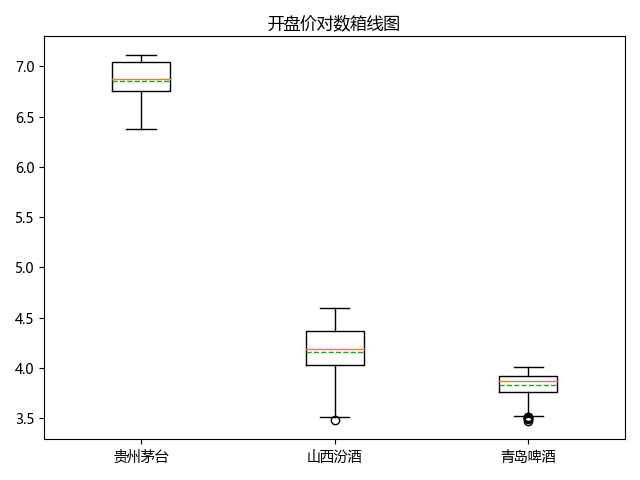
箱线图展示了数据最基本的几个统计学特征:平均值、中位数、最大值、最小值、第一分位数(前25%)、第三分位数(前75%)。箱线图往往是进行数据分析时第一个使用的图像,来简单了解数据的统计学概况。数据如果可以分类,往往还用于比较不同分类下数据的统计学信息。下图就展示了贵州茅台、山西汾酒和青岛啤酒三家企业在2019年的开盘价的箱线图:
箱线图十分简单清晰,但也仅能展示出数据的基本统计学信息,信息量较少。往往用于对数据进行一个基本的统计学展示,以及对多个类别的数据进行比较。
直方图(Histogram)
箱线图仅能看出数据的基本统计学特性,但看不出数据分布的具体细节,比如数据的具体数值在哪个区间更多、哪个区间更少。直方图就展示了数据在各个区间上的详细分布情况,如下图展示了贵州茅台在2019年开盘价取对数后的分布情况:
直方图可以较为清晰地观察到数据的分布情况。但往往只能一次观察一个数据,多个数据同时观察的话,区间重叠的部分就难以展示清楚。
密度图(Density Plot)
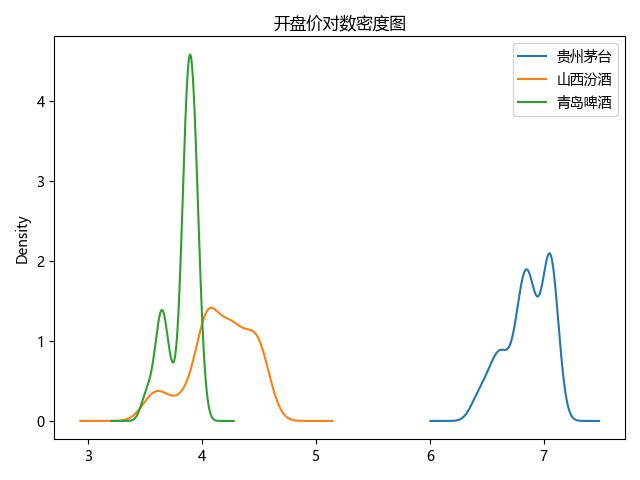
直方图表现了数据的数量分布,但其精密程度往往受到区间数量和缺失值的影响。即使区分了足够多的区间,有可能有部分数据缺失会导致对数据的分布不能得到较完整的观察。图形表现也就较差,很凹凸不平,较难看。可以用各种算法(如核密度估计)估算数据的密度分布,用线条绘制密度图。下图就展示了贵州茅台、山西汾酒和青岛啤酒2019年的开盘价取对数后的密度图:
由于用线条绘制,密度图适合在一张图上绘制多个数据的密度,从而可以比较多个数据的分布情况。但密度图仅仅能展示密度估计,不能得到精确的信息,因此往往也仅用于概览数据分布。
小提琴图(Violin Plot)
箱线图清晰简单,密度图又不那么精确,最重要的是二者的外观并不那么新颖。那么将两者组合起来就是小提琴图了。正如其名,小提琴图就是将箱线图中矩形的“箱子”变成了“小提琴”,小提琴的边缘实际上就是数据的密度分布。如下图就展示了不同型号的车辆在高速公路上的单位油耗:
小提琴图就既可以像箱线图一样展示数据的最大值、最小值、平均值等基本统计学数值,也可以像密度图一样看出数据在各个区间上的实际分布。并且如果配色得当,自然是非常亮眼的。
数据组成
很多时候一个数据中包含多个组成部分,比如成都市包含了锦江区、金牛区、高新区等各个行政区域,因此除了整个成都市的房价,往往也想观察和对比各个区域的房价。
饼图(Pie Chart)
想要查看一个数据中各个组成部分的占比,饼图是最常见的图形:
饼图可以清晰直观地展示数据中各个组成的比例,也可以像上图一样将某个类型突出展示。但如果类型过多,或者某些类型的占比过少则较难展示,不过也可以通过合并这些占比过少的类型来暂时解决。
环状图
为了让人眼前一亮,目前也有改进版的饼状图,即环状图。也就是把饼图的中间挖空,将比例展示在外面的环形,这样中间也就留出位置可以添加一些图形元素。
旭日图
除了把中间挖空,环状图还有一个优势就是可以“环环相套”,而这种嵌套结构又十分适合展示层级关系,这种环环相套并展示层级关系的环状图实际上就叫旭日图:
旭日图不仅可以比较同一层级下各个组成部分的占比,也可以比较不同层级下某个部分的占比,但一样会在种类的数量占比过少时较难展示清楚。
树形图(Tree Map)
饼图通过扇形面积表示组成的比例,环状图通过环形面积表示组成的比例,那么同样也可以使用矩形面积来表示组成的比例,这时就是树形图了。如下图就展示了某人在某月的支出在各个方面的占比情况:
华夫饼图(Waffle Chart)
上面几个通过面积大小来表示组成的比例的图都很类似,大家可能也都看腻了。华夫饼图则剑走偏锋,通过同样大小的矩形的数量来表示组成的比例。如下图就展示了某一年不同类型的汽车的销量:
柱状图(Bar Chart)
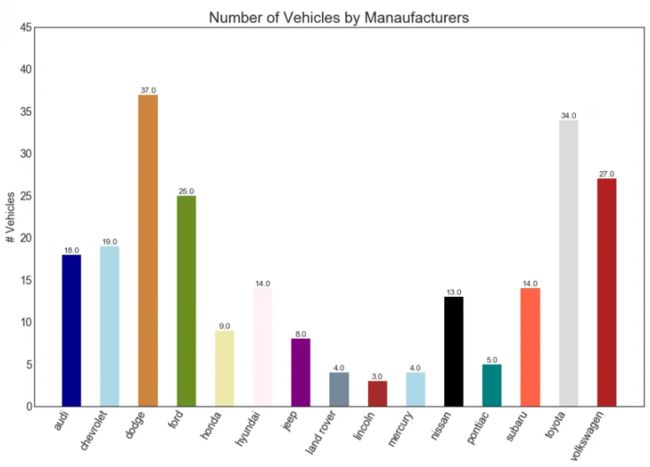
想要查看一组数据的大小,一个最简单的方式也就是柱状图,柱子的高度也就体现了数据的大小。如下图就展示了不同汽车生产商生产的汽车数量:
柱状图能很简单直观地比较数据之间的大小,但明显几根柱子还是没那么吸引眼球。
棒棒糖图(Lollipop Chart)
棒棒糖图就是一种改善了视觉效果的柱状图。正如其名,不过就是把柱子变成了“棒棒糖”。如下图就展示了不同汽车生产商的汽车油耗量:
南丁格尔玫瑰图
棒棒糖图也并不是那么引人注意,还有一种更具有视觉冲击力的图形称为南丁格尔玫瑰图,也称为鸡冠花图,实际上就是一种圆形的柱状图,相当于结合了饼图和柱状图。这种类型的图就常用于医学数据统计方面,在疫情期间就经常被各大媒体采用。如下图就展示了多个省市连续无确诊病例的天数:
堆积柱状图(Stack Bar Chart)
饼图和柱状图只能展示数据在某一种分类方式下的组成,往往一个数据还有多种不同的分类方式,因此还想比较数据在不同分类方式下组成的变化情况,这时就需要用到堆积柱状图。顾名思义,堆积柱状图本质上也是一种柱状图,即通过柱状图展示数据在一种分类方式下不同部分的数量。之后每个柱子也分成多份,体现在另一种分类方式下各部分的数量。
绝对值堆积图
绝对值堆积图中每个柱子及其不同部分的高度实际上就反映了数据的绝对数量:
上图就展示了不同汽车生产商生产各种型号的汽车的数量。由于数据往往不是平均分布,如上图中不同汽车生产商生产的汽车总量都有很大差别,因此很难直接通过肉眼比较不同汽车生产商之间,生产某一种类型的汽车的比例。
百分比堆积图
为了展示和对比数据在不同分类方式下不同组成的比例,就要依赖百分比堆积图。百分比堆积图中柱子的高度体现的就是百分比,即不同部分占据的比例。也就是将数据在一种分类方式下的数据总量归一化到100%,之后就好比较在另一种分类方式下某个组分的比例:
如上图,尽管不同业务员的销售总量不一致,但经过归一化为百分比后,就可以比较不同业务员销售饮料和点心的比例的差别。
堆积面积图(Stack Area Chart)
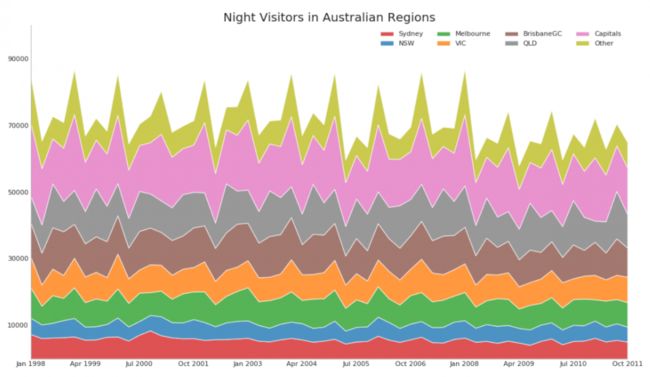
往往很想了解数据中各个组分随着时间的变化,也就是说时间也常常是数据分类的一种方式。如果想比较的也就只是少数几个时间段的数据,即分类较少时,柱状图就很够用了。但若比较的时间范围很长,柱状图就很难更清晰地展示出数据组分的变化,此外一张图上数十个柱子也挺难看的,这时就要用到堆积面积图了。堆积面积图实际上相当于折线图和堆叠柱状图的组合:
堆积面积图看起来就像多个堆叠起来的折线图,因此每个点的值就是两条折线之间的面积(或直接就是Y值的差值)。该图可以比较清晰地对比多个部分在很长的时间段内的变化。
百分比堆积面积图
类似百分比柱状图,堆积面积图一样也可以将总量归一化到100%,比较各个部分比例随时间的变化:
分组柱状图(Grouped Bar Chart)
与堆积柱状图类似,一个柱子的不同类别也可以左右“堆积”起来,那也就是分组柱状图了:
显然分组柱状图可以更方便地比较不同类别之间的绝对数量。
双向柱状图(Bidirectional Bar Chart)
对于性别这种典型的二分类,或分类很明显具有相对性(如收入和支出),也可以通过双向柱状图来进行比较。如下图就展示了2002年香港不同年龄、男性和女性的人口图:
漏斗图(Funnel Chart)
数据的组成往往是具有层级结构的,而为了展示出数据中每一层最被人关心的部分,那就要用到漏斗图了。下图就展示了“复仇者联盟3”在豆瓣上的评分情况:
漏斗图展示出了每一层结构中最被人关注的那一部分,并且垂直比较不同层之间的数量,可以对比出数据在哪一层减少的最多。
词云(Word Cloud)
即使是文字,也都可以展示出很多东西,词云就是目前经常使用的一种表示方式,主要就通过文字的大小,来体现出占比或重要性。比如下图就展示出中国少数民族的人口比例:
词云图目前常用于进行用户画像,即通过分析某个用户的行为和资料,通过词云图展示与该用户相关的关键词,查看分析该用户的主要特征。
地图
凡是涉及到地理的数据,与实际的地图进行组合当然是最真实和最有表现力的。
热力地图
地图上各区域添加不同的颜色,就能展示某种数据在不同区域的大小,如下图就展示了截止2020年12月18日中国新冠的累积确诊病例:
轨迹地图
一个很重要的涉及到地理的数据就是路线,因此经常在地图上通过各种线条来体现从A地到B地的路线,也就是轨迹地图。如下图就展示了春运期间,从北京出发的路线分别都去了何处:
数据比较
在展示数据分布、查看数据组成时,其实很多时候就已经在对数据进行比较了。一张图片上展示多个箱线、多条密度曲线、多组条柱时,就可以同时观察几个数据的分布或组成情况。但简单堆积和叠加这些图像并不能比较数据之间的很多细节,下面就是一些常用于数据比较的图形。
折线图(Line Chart)
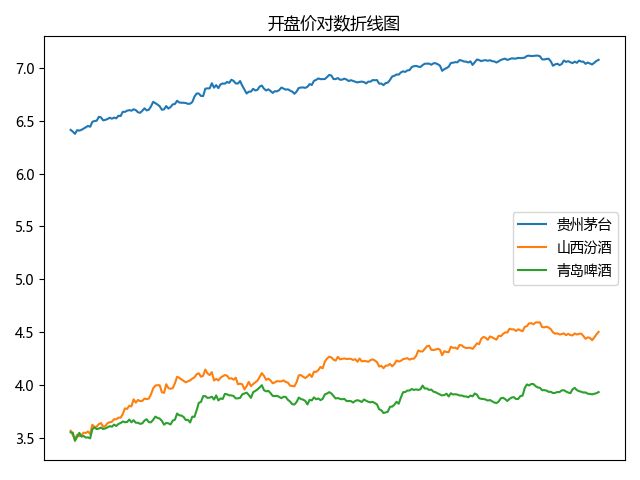
一种最常见的数据分类方式就是时间,也就是经常需要查看数据随时间的变化。折线图就是最常见的查看数据随时间变化的图形,如下图就展示了贵州茅台、山西汾酒和青岛啤酒2019年的开盘价取对数后的折线图:
折线图可以很清晰地看出数据随时间的走势,但当时间节点很多的时候,也就难以展示出每个时间点具体的数值了。
瀑布图(Waterfall Chart)
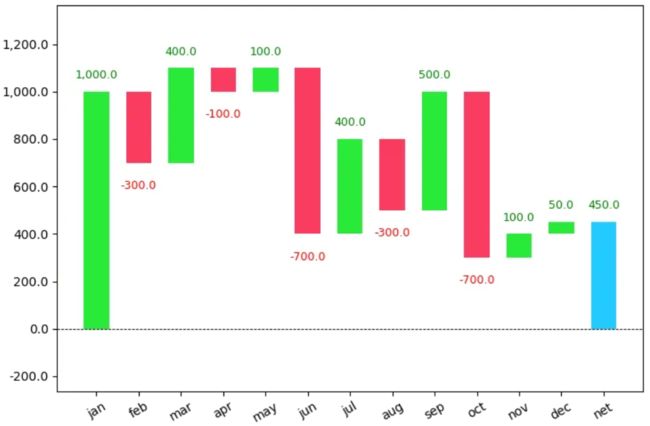
当想要查看金额类的数据随时间的变化时,比如股票价格,最常见的图反而是瀑布图:
瀑布图不仅展示了数据的值,还展示了每一个时刻的数据与上一时刻相比的变化(上涨或下跌),并通过颜色强调了变化的种类
K线图(Waterfall Chart)
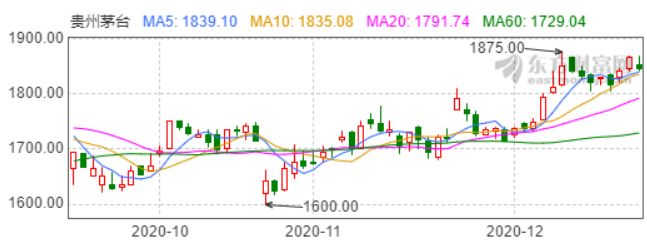
一张瀑布图也就仅可以展示一类数据,比如股票的开盘价,因此K线图就出现了。K线图就相当于瀑布图和箱线图的组合。首先同样以瀑布图思路通过颜色(阳线阴线)强调出数据的变化方向,此外也像箱线图一样再添加一些元素(伸出的触须),展示出股价的最高价、最低价等信息。如下图就是一段时间内贵州茅台的K线图:
雷达图(Radar Chart)
之前提到的各种柱状图可以通过堆叠、分组等比较数据在不同分类方式下各个组分的区别。但柱状图往往不那么亮眼,雷达图则一样可以达到类似的目的。如下图就展示了预算和实际开销在各个方面的数值:
雷达图一样可以很清晰地体现某个数据的不同组成部分的占比。
坡度图(Slope Chart)
很多时候仅仅想要比较和强调两个时间点上某个数据的变化,比如改革开放30年前后中国GDP总量的变化等。这时常用的就是坡度图,如下图就展示了1952年到1957年,各个大洲人均GDP的变化:
坡度图强调并比较了数据在两个时间点上变化的方向和幅度,实际上也是一种简化版的折线图。
桑基图(Sankey diagram)
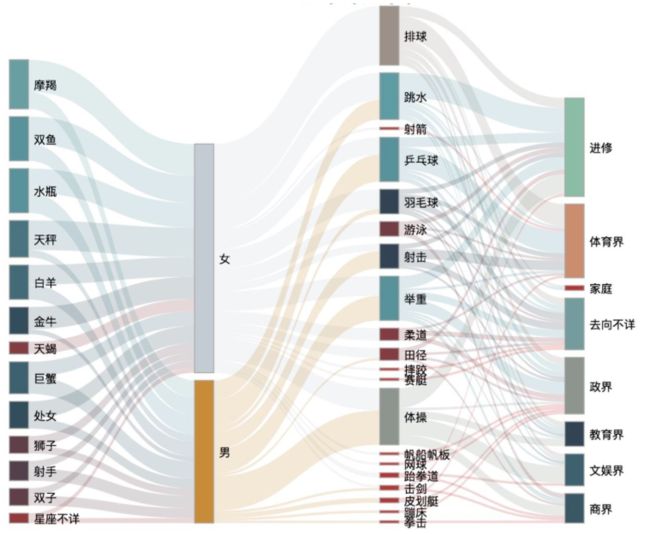
数据往往也都是有去向的,比如总想知道把产品添加到购物车中的客户,有多少最后真正下单了,又有多少下了单的客户最后真正购买了。这种展示数据流向的最佳图表也就非桑基图莫属了。如下图就展示了各个星座男生女生分别是多少,之后不同星座的人又去干了什么:
桑基图就是流程图的一种量化表示形式,能够很清晰地看出数据的流向。
数据关系
很多时候得到的数据并不只是一个维度上的,往往想要比较数据在不同维度上的关系,进而去推断和预测一些东西,比如年龄和身高、性别和收入等。时间就往往就是一个很重要的维度,因此之前的数据比较中就提到了通过折线图反映数据随时间的变化。能表现数据在不同维度上的关系的图表还有很多。
散点图(Scatter Plot)
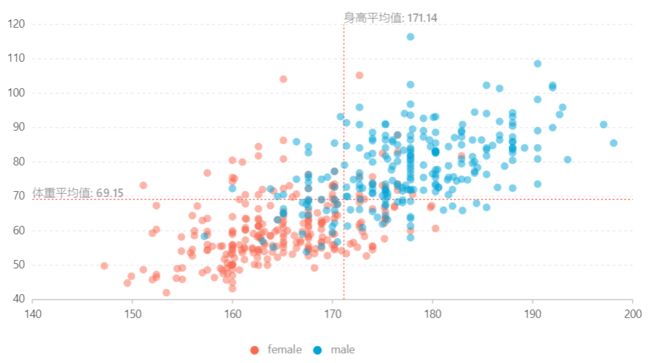
若想查看数据在两个维度上的关系,最经典也最常见的也就是散点图了。如下图就以身高为X轴、体重为Y轴,绘制了身高和体重的散点图,并通过颜色对男女进行了区分:
散点图能够比较快速直观地展示数据两个维度上的数值,并能大致观察出数据在这两个维度上是否具有相关性。但散点图仅能展示两个维度上的数据,最多再通过点的颜色、形状等,添加上第三个离散维度的信息。并且当数据点过多、过密时,也较难区分。
散点气泡图
散点图仅能展示数据在两个维度上的数据,但点也是有大小的,因此目前一个经常应用的组合就是散点图+气泡图。就是在散点图的基础上,通过点(气泡)的大小来体现第三个维度上的信息。如下图就是澎湃网展示的“侵犯公民个人信息案件”的量刑数据:
图片中每个点代表一个案件,案件分为3大类分布在X轴上,点在y轴的位置体现了案件的罚金,点的大小则体现了案件的获刑时间。
相关性热图(Correlogram)
散点图和气泡图的目的往往就是观察数据在两、三个维度上的相关性,无法同时反映数据所有维度之间的相关性,并且在数据过多时也都较难展示。而数学上还有很多可以衡量数据相关性的统计量,比如皮尔逊相关系数等。相关性热图就是通过彩色色块来表示数据相关系数的图表。如下图就展示了mtcars数据集中,汽车各种参数之间的相关系数:
相关性热图就是将数据的各个维度进行成对比较,而斜对角线上就是两个相同的维度,相关性系数也就一定为1,表示完全正相关;同时该图也是对称的,第i行第j列的数值和颜色与第j行第i列一定是相同的。
成对比较图(Pairwise Plot)
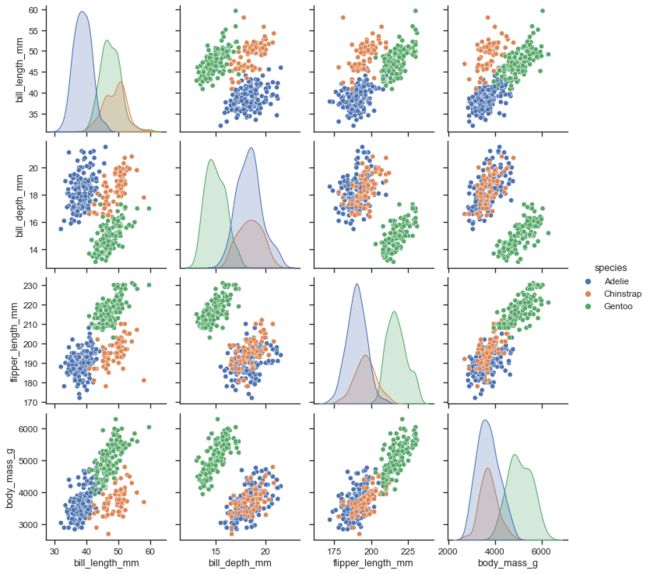
相关性热图仅展示了计算出来的数据各个维度之间的相关系数,也并不能体现数据的很多细节。成对比较图则展示了数据各个维度之间更加详细的信息。对于n维数据,成对比较图实际上是n*n个散点图的组合,第i行第j列上的图就是分别以数据第i个维度和第j个维度作为X轴和Y轴的散点图,可以查看数据在这两个维度上的相关性。而对角线上是数据的同一个维度,散点图也没有任何意义,因此对角线上的图片就更换为数据在该维度的密度分布图。如下图就展示了三种鸟类喙长、喙深、蹼长、体重四种数据之间的关系:
成对比较图比较复杂,但几乎对数据的各个维度都进行了展示,既可以成对比较数据的相关性,也可以查看数据在某个维度上的密度分布。
和弦图(Chord Diagram)
相关性热图仅仅通过不同的颜色展示了数据之间的相关性,看起来比较单调。而和弦图则将数据围成一圈,数据之间通过条带两两连接起来,条带的宽度体现数据的关联程度,关联程度越大条带越宽。比如下图就展示了Uber用户在各个地区之间进行通勤的情况:
图中每个城市弧形的大小表示了该城市的交通流量,每两个城市之间都有一条边连接,边的宽度则表示了这两个城市之间的交通流量。有些城市还有连向自己的边,则表示交通的起点和终点都在该城市内。可以看出和弦图就相当于环状图和桑基图的组合,也就是环形桑基图,既可以体现数据每个部分的大小,也可以看出数据不同部分之间的关联程度。
数据可视化之道
上面已经展示并简单描述了很多数据展示的方式,但个人认为这些都只是数据可视化之术,任何图形大家看习惯之后也都不那么容易引起注意了。因此更重要的还是要体会数据可视化之道,之后能够自己尝试组合创造出更新颖的图表,也许更容易吸引眼球。下面简单记录一些自己的体会。
图表往往也就是各种元素的组合。这一点在使用各种编程语言绘图时更加明显,比如使用Python中各种包(matplotlib、ploty、seaborn等)进行绘图时,一定要正确设置图标的各种属性。那么对数据进行可视化,本质上就是要将数据通过图表的各种元素表现出来。因此第一件事就是要明确数据的各种特性与图表的各种元素的对应关系。
首先数据就有连续和离散两种形式,那么对应地图表的元素也往往有这两种形式。图表中各种形状的位置(上下、前后、左右等)、大小(点和圆的半径、线条的粗细、扇形的弧度、各种形状的面积等)就都可以是连续的,对应地也就可以用来表现连续数值,比如GDP、收入等。其次图表中也有离散的元素,比如形状(圆形、扇形、方形、叉形等)、颜色(红、黄、蓝等),对应也可以体现离散的数据,比如不同来源、不同分类的数据。
值得注意的是,无论是数据还是图表的元素,离散和连续都是可以互相转换的。比如可以通过自定义数据区间将连续的数据离散化;也可以通过合适的过渡色,将不同的颜色也连续化。
较为传统的表示方式都是在正交坐标系中展示各种图形,而目前看来一个比较新颖的转换点就在将正交坐标系转换为极坐标。比如曾经的直方图转换到极坐标下就是南丁格尔玫瑰图。矩形的图片经过转换后变为圆形,往往能够让人眼前一亮。
此外,一种图表能展示的数据往往并不足以说明全部问题,常常还可以将多种图表的思路进行组合,从而达到同时在多个方面展示数据的目的。比如上文中提到的小提琴图(箱线图+密度图)、旭日图(环状图+树形图)等。也可以对多张图表进行合适的分组、堆叠,从而达到比较多组数据的目的。因此多尝试图表的组合也是一种创新思路。不过这时需要注意,如果一张图片的信息量过大,也是很难让人抓住重点的。
最近发现蚂蚁金服开发了一系列数据可视化的工具(AntV),其中G2就包含很多数据可视化图标的示例,可以随时查阅:http://antv-2018.alipay.com/zh-cn/g2/3.x/demo/index.html
AntV也一样对图表进行了分类,并进行了简单描述,记录一下以备查阅:http://antv-2018.alipay.com/zh-cn/vis/chart/index.html