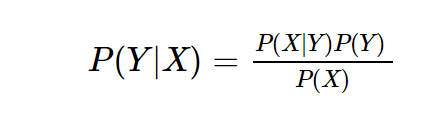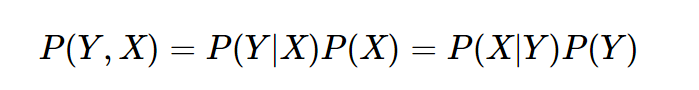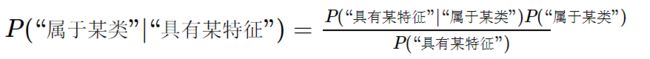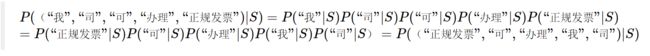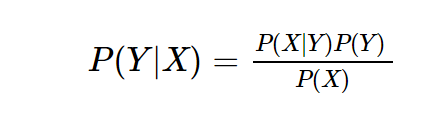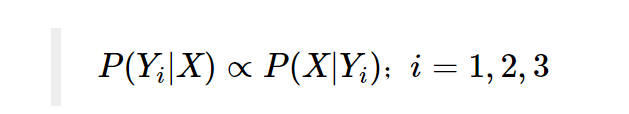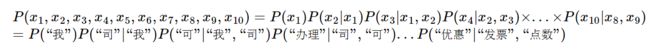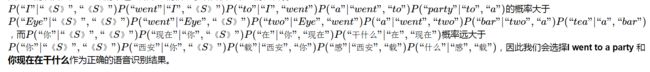一、 贝叶斯公式
1、引言
贝叶斯方法是一个历史悠久,朴素贝叶斯中的朴素一词的来源就是假设各特征之间相互独立。这一假设使得朴素贝叶斯算法变得简单,但有时会牺牲一定的分类准确率。当然有着坚实的理论基础的方法,同时处理很多问题时直接而又高效,很多高级自然语言处理模型也可以从它演化而来。因此,学习贝叶斯方法,是研究自然语言处理问题的一个非常好的切入口。
2、贝叶斯公式
贝叶斯公式其实很简单,但是很常用,就一行:
而它其实是由以下的联合概率公式推导出来:
其中 P(Y)叫做先验概率, P(Y|X)叫做后验概率, P(Y,X)叫做联合概率。这就是有关贝叶斯的所有核心公式。
3、用机器学习的视角理解贝叶斯公式
在机器学习的视角下,我们把 X 理解成“具有某特征”,把 Y理解成“类别标签”(一般机器学习为题中都是X=>特征, Y=>结果对吧)。在最简单的二分类问题(是与否判定)下,我们将 Y理解成“属于某类”的标签。于是贝叶斯公式就变形成了下面的样子:
我们简化解释一下上述公式:
P(“属于某类”|“具有某特征”)=在已知某样本“具有某特征”的条件下,该样本“属于某类”的概率。所以叫做『后验概率』。
P(“具有某特征”|“属于某类”)= 在已知某样本“属于某类”的条件下,该样本“具有某特征”的概率。
P(“属于某类”)=(在未知某样本具有该“具有某特征”的条件下,)该样本“属于某类”的概率。所以叫做『先验概率』。
P(“具有某特征”)=(在未知某样本“属于某类”的条件下,)该样本“具有某特征”的概率。
而我们二分类问题的最终目的就是要判断 P(“属于某类”|“具有某特征”) 是否大于1/2就够了。贝叶斯方法把计算“具有某特征的条件下属于某类”的概率转换成需要计算“属于某类的条件下具有某特征”的概率,而后者获取方法就简单多了,我们只需要找到一些包含已知特征标签的样本,即可进行训练。而样本的类别标签都是明确的,所以贝叶斯方法在机器学习里属于有监督学习方法。
这里再补充一下,一般『先验概率』、『后验概率』是相对出现的,比如 P(Y)与 P(Y|X) 是关于 Y的先验概率与后验概率, P(X)与 P(X|Y)是关于 X的先验概率与后验概率。
4、垃圾邮件识别
我们可以通过一个例子来对邮件进行分类,识别垃圾邮件和普通邮件,如果我们选择使用朴素贝叶斯分类器,那目标就是判断 P(“垃圾邮件”|“具有某特征”) 是否大于1/2。现在假设我们有垃圾邮件和正常邮件各1万封作为训练集。需要判断以下这个邮件是否属于垃圾邮件:
例如: “我司可办理正规发票(保真)17%增值税发票点数优惠!”
也就是判断概率 P(“垃圾邮件”|“我司可办理正规发票(保真)17%增值税发票点数优惠!”)是否大于1/2。我们不难发现:通过上述的理解,也就是将其转换成的这个概率,计算的方法:就是写个计数器,然后+1 +1 +1统计出所有垃圾邮件和正常邮件中出现这句话的次数啊。也就是:
5、分词
我们在做机器学习时,不难发现训练集是有限的,而句子的可能性则是无限的。所以覆盖所有句子可能性的训练集是不存在的。因此按我们正常的经验理解,两句话意思相近并不强求非得每个字、词语都一样。比如“我司可办理正规发票,17%增值税发票点数优惠!”,这句话就比之前那句话少了“(保真)”这个词,但是意思基本一样。如果把这些情况也考虑进来,那样本数量就会增加,这就方便我们计算了。于是,我们可以不拿句子作为特征,而是拿句子里面的词语(组合)作为特征去考虑。比如“正规发票”可以作为一个单独的词语,“增值税”也可以作为一个单独的词语等等。
句子 “我司可办理正规发票,17%增值税发票点数优惠!”就可以变成( “我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”))。
于是当我们接触到了中文NLP中,其中最为重要的技术之一:分词!!!也就是把一整句话拆分成更细粒度的词语来进行表示。另外,分词之后去除标点符号、数字甚至无关成分(停用词)是特征预处理中的一项技术。我们观察(“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”),这可以理解成一个向量:向量的每一维度都表示着该特征词在文本中的特定位置存在。这种将特征拆分成更小的单元,依据这些更灵活、更细粒度的特征进行判断的思维方式,在自然语言处理与机器学习中都是非常常见又有效的。因此贝叶斯公式就变成了:
6、 条件独立假设
我们还是以前面的垃圾邮件分类为例,概率 P((“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)|“垃圾邮件”) 依旧比较难求,我们于是引进一个很朴素的近似。为了让公式显得更加紧凑,我们令字母S表示“垃圾邮件”,令字母H表示“正常邮件”。近似公式如下:
这就是经常讲的条件独立假设。基于“正常邮件”的条件独立假设的式子与上式类似,接着,将条件独立假设代入上面两个相反事件的贝叶斯公式。于是我们就只需要比较以下两个式子的大小:
接下来,我们只需要分别统计各类邮件中该关键词出现的概率就可以了。
统计次数非常方便,而且样本数量足够大,算出来的概率比较接近真实。于是垃圾邮件识别的问题就可解了。
二、朴素贝叶斯
1、朴素贝叶斯(Naive Bayes),“Naive”在何处?
加上条件独立假设的贝叶斯方法就是朴素贝叶斯方法(Naive Bayes)。将句子(“我”,“司”,“可”,“办理”,“正规发票”) 中的 (“我”,“司”)与(“正规发票”)调换一下顺序,就变成了一个新的句子(“正规发票”,“可”,“办理”, “我”, “司”)。新句子与旧句子的意思完全不同。但由于乘法交换律,朴素贝叶斯方法中算出来二者的条件概率完全一样!计算过程如下:
也就是说,正如朴素贝叶斯,“我司可办理正规发票”与“正规发票可办理我司”完全相同。朴素贝叶斯失去了词语之间的顺序信息。这就相当于把所有的词汇扔进到一个袋子里随便搅和,贝叶斯都认为它们一样。因此这种情况也称作词袋子模型(bag of words)。
2、 简单高效
我们之前的垃圾邮件向量(“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”),其中每个词都不重复。而这在现实中其实很少见。因为如果文本长度增加,或者分词方法改变,必然会有许多词重复出现,因此需要对这种情况进行进一步探讨。比如以下这段邮件:
“代开发票。增值税发票,正规发票。” 分词后为向量: (“代开”,“发票”,“增值税”,“发票”,“正规”,“发票”)
其中“发票”重复了三次。
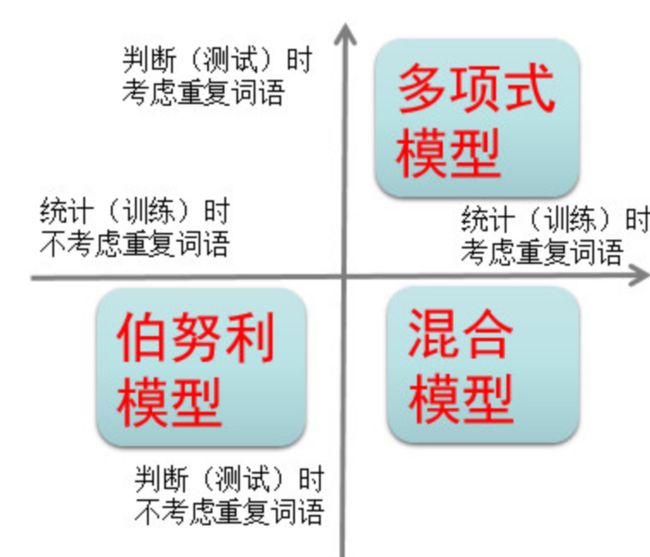
3、处理重复词语的三种方式
(1)、多项式模型:
如果我们考虑重复词语的情况,也就是说,重复的词语我们视为其出现多次,直接按条件独立假设的方式推导,则有:
在统计计算P(“发票”|S)时,每个被统计的垃圾邮件样本中重复的词语也统计多次。
我们不难发现:这个多次出现的结果,出现在概率的指数/次方上,因此这样的模型叫作多项式模型。
(2)、伯努利模型
另一种更加简化的方法是将重复的词语都视为其只出现1次,
P((“代开”,“发票”,“增值税”,“发票”,“正规”,“发票”)|S)=P(“发票”|S)P(“代开””|S)P(“增值税”|S)P(“正规”|S)
统计计算 P(“词语”|S)时也是如此。
我们把这样的模型叫作伯努利模型(又称为二项独立模型)。这种方式更加简化与方便。当然它丢失了词频的信息,因此效果可能会差一些。
(3)、 混合模型
第三种方式是在计算句子概率时,不考虑重复词语出现的次数,但是在统计计算词语的概率P(“词语”|S)时,却考虑重复词语的出现次数,这样的模型可以叫作混合模型。接下来我们通过下图展示三种模型的关系。
这三种模型的具体实践中采用哪种模型,关键看具体的业务场景,一个简单经验是,对于垃圾邮件识别,混合模型更好些。
4、去除停用词与选择关键词
我们继续观察(“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”) 这句话。其实,像“我”、“可”之类词其实非常中性,无论其是否出现在垃圾邮件中都无法帮助判断的有用信息。所以可以直接不考虑这些典型的词。这些无助于我们分类的词语叫作“停用词”(Stop Words)。这样可以减少我们训练模型、判断分类的时间。 于是之前的句子就变成了(“司”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”) 。
我们进一步分析。以人类的经验,其实“正规发票”、“发票”这类的词如果出现的话,邮件作为垃圾邮件的概率非常大,可以作为我们区分垃圾邮件的“关键词”。而像“司”、“办理”、“优惠”这类的词则有点鸡肋,可能有助于分类,但又不那么强烈。如果想省事做个简单的分类器的话,则可以直接采用“关键词”进行统计与判断,剩下的词就可以先不管了。于是之前的垃圾邮件句子就变成了(“正规发票”,“发票”) 。这样就更加减少了我们训练模型、判断分类的时间,速度非常快。“停用词”和“关键词”一般都可以提前靠人工经验指定。不同的“停用词”和“关键词”训练出来的分类器的效果也会有些差异。
5、平滑技术
我们来说个问题(中文NLP里问题超级多,哭瞎T_T),比如在计算以下独立条件假设的概率:
P((“我”,“司”,“可”,“办理”,“正规发票”)|S) =P(“我”|S)P(“司”|S)P(“可”|S)P(“办理”|S)P(“正规发票”|S)
我们扫描一下训练集,发现“正规发票”这个词从出现过!!!,于是 P(“正规发票”|S)=0 …问题严重了,整个概率都变成0了!!!朴素贝叶斯方法面对一堆0,很凄惨地失效了…更残酷的是这种情况其实很常见,因为哪怕训练集再大,也可能有覆盖不到的词语。本质上还是样本数量太少,不满足大数定律,计算出来的概率失真*。为了解决这样的问题,一种分析思路就是直接不考虑这样的词语,但这种方法就相当于默认给P(“正规发票”|S)赋值为1。其实效果不太好,大量的统计信息给浪费掉了。我们进一步分析,既然可以默认赋值为1,为什么不能默认赋值为一个很小的数?这就是平滑技术的基本思路,依旧保持着一贯的作风,朴实/土但是直接而有效。对于伯努利模型,P(“正规发票”|S)的一种平滑算法是:
对于多项式模型,P(“正规发票”| S)的一种平滑算法是:
其实平滑技术的种类其实非常多,只不过所有的平滑技术都是给未出现在训练集中的词语一个估计的概率,而相应地调低其他已经出现的词语的概率。另外,平滑技术是因为数据集太小而产生的现实需求。如果数据集足够大,平滑技术对结果的影响将会变小。
6、为什么不直接匹配关键词来识别垃圾邮件?
谈到这里,有很多学习NLP的同学肯定会有一些疑惑:“何必费这么大劲算那么多词的概率?直接看邮件中有没有‘代开发票’、‘转售发票’之类的关键词难道行不通吗?如果关键词比较多就可以默认为垃圾邮箱。”其实关键词匹配的方法如果有效的话真不必用朴素贝叶斯。毕竟这种方法简单嘛,就是一个字符串匹配。从历史来看,之前没有贝叶斯方法的时候主要也是用关键词匹配。但是这种方法准确率太低。我们在工作项目中也尝试过用关键词匹配的方法去进行文本分类,发现大量误报。感觉就像扔到垃圾箱的邮件99%都是正常的!这样的效果不忍直视。而加一个朴素贝叶斯方法就可能把误报率拉低近一个数量级,体验好得不要不要的。另一个原因是词语会随着时间不断变化。发垃圾邮件的人也不傻,当他们发现自己的邮件被大量屏蔽之后,也会考虑采用新的方式,如变换文字、词语、句式、颜色等方式来绕过反垃圾邮件系统。而朴素贝叶斯方法却显示出无比的优势。因为它是基于统计方法的,只要训练样本中有更新的垃圾邮件的新词语,哪怕它们是火星文,都能自动地把哪些更敏感的词语(如“髮”、“㊣”等)给凸显出来,并根据统计意义上的敏感性给他们分配适当的权重 ,这样就不需要什么人工了,非常省事。你只需要时不时地拿一些最新的样本扔到训练集中,重新训练一次即可。
7、在实际工程的一些技巧
(1)、取对数
还是我们之前提到的用来识别垃圾邮件的方法是比较以下两个概率的大小(字母S表示“垃圾邮件”,字母H表示“正常邮件”):
但这里进行了很多乘法运算,计算的时间开销比较大。尤其是对于篇幅比较长的邮件,几万个数相乘起来还是非常花时间的。如果能把这些乘法变成加法则方便得多。刚好数学中的对数函数log就可以实现这样的功能。两边同时取对数(本文统一取底数为2),则上面的公式变为:
或许有同学会说:“做对数运算岂不会也很花时间?”的确如此,但是可以在训练阶段直接计算 logP,然后把他们存在一张大的hash表里。在判断的时候直接提取hash表中已经计算好的对数概率,然后相加即可。这样使得判断所需要的计算时间被转移到了训练阶段,实时运行的时候速度就比之前快得多,这可不止几个数量级的提升。
(2)、转换为权重
对于二分类,我们还可以继续提高判断的速度。既然要比较 logC和 logC¯¯¯¯ 的大小,那就可以直接将上下两式相减,并继续化简:
logC/C¯¯¯¯如果大于0则属于垃圾邮件。我们可以把其中每一项作为其对应词语的权重,比如logP(“发票”|S)P(“发票”|H)就可以作为词语“发票”的权重,权重越大就越说明“发票”更可能是与“垃圾邮件”相关的特征。这样可以根据权重的大小来评估和筛选显著的特征,比如关键词。而这些权重值可以直接提前计算好而存在hash表中 。判断的时候直接将权重求和即可。关键词hash表的样子如下,左列是权重,右列是其对应的词语,权重越高的说明越“关键”:
(3)、选取topk的关键词
前文说过可以通过提前选取关键词来提高判断的速度。有一种方法可以省略提前选取关键词的步骤,就是直接选取一段文本中权重最高的K个词语,将其权重进行加和。比如Paul Graham 在《黑客与画家》中是选取邮件中权重最高的15个词语计算的。通过权重hash表可知,如果是所有词语的权重,则权重有正有负。如果只选择权重最高的K个词语,则它们的权重基本都是正的。所以就不能像之前那样判断 logC/C¯¯¯¯是否大于0来区分邮件了。而这需要依靠经验选定一个正数的阈值(门槛值) ,依据 logC/C¯¯¯¯与该门槛值的大小来识别垃圾邮件。如下图所示,蓝色点代表垃圾邮件,绿色点代表正常邮件,横坐标为计算出来的 logC/C¯¯¯¯值,中间的红线代表阈值。
(4)、分割样本
选取topk个词语的方法对于篇幅变动不大的邮件样本比较有效。但是对篇幅过大或者过小的邮件则会有判断误差。比如这个垃圾邮件的例子:(“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)。分词出了10个词语,其中有“正规发票”、“发票”2个关键词。关键词的密度还是蛮大的,应该算是敏感邮件。但因为采用最高15个词语的权重求和,并且相应的阈值是基于15个词的情况有效,可能算出来的结果还小于之前的阈值,这就造成漏判了。类似的,如果一封税务主题的邮件有1000个词语,其中只有“正规发票”、“发票”、“避税方法”3个权重比较大的词语,它们只是在正文表述中顺带提到的内容。关键词的密度被较长的篇幅稀释了,应该算是正常邮件。但是却被阈值判断成敏感邮件,造成误判了。这两种情况都说明topk关键词的方法需要考虑篇幅的影响。这里有许多种处理方式,它们的基本思想都是选取词语的个数及对应的阈值要与篇幅的大小成正比,本文只介绍其中一种方方法:
1、对于长篇幅邮件,按一定的大小,比如每500字,将其分割成小的文本段落,再对小文本段落采用topk关键词的方法。只要其中有一个小文本段落超过阈值就判断整封邮件是垃圾邮件。
2、对于超短篇幅邮件,比如50字,可以按篇幅与标准比较篇幅的比例来选取topk,以确定应该匹配关键词语的个数。比如选取 50/500×15≈2个词语进行匹配,相应的阈值可以是之前阈值的 2/15 。以此来判断则更合理。
(5)、位置权重
到目前为止:我们对词语权重求和的过程都没有考虑邮件篇章结构的因素。比如“正规发票”如果出现在标题中应该比它出现在正文中对判断整个邮件的影响更大;而出现在段首句中又比其出现在段落正文中对判断整个邮件的影响更大。所以可以根据词语出现的位置,对其权重再乘以一个放大系数,以扩大其对整封邮件的影响,提高识别准确度。比如一封邮件其标题是“正规发票”(假设标题的放大系数为2),段首句是“发票”,“点数”,“优惠”(假设段首的放大系数为1.5),剩下的句子是(“我”,“司”,“可”,“办理”,“保真”)。则计算 logC/C¯¯¯¯时的公式就可以调整为:
8、贝叶斯方法的思维方式
(1)、逆概问题
我们重新看一眼贝叶斯公式:
先不考虑先验概率 P(Y)与P(X),观察两个后验概率 P(Y|X)与P(X|Y),可见贝叶斯公式能够揭示两个相反方向的条件概率之间的转换关系。从贝叶斯公式的发现历史来看,其就是为了处理所谓“逆概”问题而诞生的。比如 P(Y|X)不能通过直接观测来得到结果,而 P(X|Y) 却容易通过直接观测得到结果,就可以通过贝叶斯公式从间接地观测对象去推断不可直接观测的对象的情况。也就是说基于邮件的文本内容判断其属于垃圾邮件的概率不好求(不可通过直接观测、统计得到),但是基于已经搜集好的垃圾邮件样本,去统计(直接观测)其文本内部各个词语的概率却非常方便。这就可以用贝叶斯方法。另外,基于样本特征去判断其所属标签的概率不好求,但是基于已经搜集好的打上标签的样本(有监督),却可以直接统计属于同一标签的样本内部各个特征的概率分布。因此贝叶斯方法的理论视角适用于一切分类问题的求解。
(2)、处理多分类问题
前面我们一直在探讨二分类(判断题)问题,现在可以引申到多分类(单选题)问题了。还是用邮件分类的例子,这是现在不只要判断垃圾邮件,还要将正常邮件细分为私人邮件、工作邮件。现在有这3类邮件各1万封作为样本。需要训练出一个贝叶斯分类器。这里依次用 Y1,Y2,Y3表示这三类邮件,用 X表示被判断的邮件。套用贝叶斯公式有:
通过比较3个概率值的大小即可得到 X所属的分类。发现三个式子的分母 P(X)一样,比较大小时可以忽略不计,于是就可以用下面这一个式子表达上面3式:
其中 ∝表示“正比于”。而 P(X|Yi)则有个特别高逼格的名字叫做“似然函数”。我们上大学的时候也被这个名字搞得晕晕乎乎的,其实它也是个概率,直接理解成“ P(Yi|X)的逆反条件概率” 就方便了。这里只是以垃圾邮件3分类问题举了个例子,对于任意多分类的问题都可以用这样的思路去理解。比如新闻分类、情感喜怒哀乐分类等等。
(3)、先验概率的问题
在垃圾邮件的例子中,先验概率都相等, P(Y1)=P(Y2)=P(Y3)=10000/30000=1/3,所以上面是式子又可以进一步化简:
只需比较右边式子(也就是“似然函数”)的大小就可以了。这种方法就是传说中的最大似然法:不考虑先验概率而直接比较似然函数。关于选出最佳分类 Yi是否要考虑先验概率 P(Yi)的问题,曾经在频率学派和贝叶斯学派之间产生了激烈的教派冲突。统计学家(频率学派)说:我们让数据自己说话。言下之意就是要摒弃先验概率。而贝叶斯学派支持者则说:数据会有各种各样的偏差,而一个靠谱的先验概率则可以对这些随机噪音做到健壮。如果还用贝叶斯方法,就要在似然函数后面乘上先验概率。比如之前用最大似然法算出 Y1垃圾邮件的概率大,但是因为 P(Y1)特别小,用贝叶斯方法得出的结果是 Y2私人邮件的概率大。那相信哪个呢?其实,我们删掉了部分带标签的样本,从计算结果看 P(Y1),P(Y2),P(Y3)的概率分布变化了,但实际上这三个类别的真实分布应该是一个客观的状态,不应该因为我们的计算方法而发生变化。所以是我们计算出来的先验概率失真,应该放弃这样计算出来的先验概率,而用最大似然法。但即便我们不删掉一半垃圾邮件,这三类邮件的分布就真的是1:1:1那样平均吗?那也未必。我们只是按1:1:1这样的方式进行了抽样而已,真正在邮箱里收到的这三类邮件的分布可能并不是这样。也就是说,在我们对于先验概率一无所知时,只能假设每种猜测的先验概率是均等的(其实这也是人类经验的结果),这个时候就只有用最大似然了。在现实运用过程中如果发现最大似然法有偏差,可以考虑对不同的似然函数设定一些系数或者阈值,使其接近真实情况。但是,如果我们有足够的自信,训练集中这三类的样本分布的确很接近真实的情况,这时就应该用贝叶斯方法。难怪前面的贝叶斯学派强调的是“靠谱的先验概率”。所以说贝叶斯学派的适用范围更广,关键要先验概率靠谱,而频率学派有效的前提也是他们的先验概率同样是经验统计的结果。
9、(朴素)贝叶斯方法的常见应用
我们讲了这么多理论的问题,咱们就可以探讨一下(朴素)贝叶斯方法在自然语言处理中的一些常见应用了。以下只是从原理上进行探讨,对于具体的技术细节顾及不多。
(1)、褒贬分析
一个比较常见的应用场景是情感褒贬分析。比如你要统计微博上人们对一个新上映电影的褒贬程度评价:好片还是烂片。但是一条一条地看微博是根本看不过来,只能用自动化的方法。我们可以有一个很粗略的思路:
1、 首先是用爬虫将微博上提到这个电影名字的微博全都抓取下来,比如有10万条。
2、然后用训练好的朴素贝叶斯分类器分别判断这些微博对电影是好评还是差评。
3、最后统计出这些好评的影评占所有样本中的比例,就能形成微博网友对这个电影综合评价的大致估计。
接下来的核心问题就是训练出一个靠谱的分类器。首先需要有打好标签的文本。这个好找,豆瓣影评上就有大量网友对之前电影的评价,并且对电影进行1星到5星的评价。我们可以认为3星以上的评论都是好评,3星以下的评论都是差评。这样就分别得到了好评差评两类的语料样本。剩下就可以用朴素贝叶斯方法进行训练了。基本思路如下:
1、训练与测试样本:豆瓣影评的网友评论,用爬虫抓取下100万条。
2、标签:3星以上的是好评,3星以下的是差评。
3、特征:豆瓣评论分词后的词语。一个简单的方法是只选择其中的形容词,网上有大量的情绪词库可以为我们所用。
4、然后再用常规的朴素贝叶斯方法进行训练。
但是由于自然语言的特点,在提取特征的过程当中,有一些tricks需要注意:
1、 对否定句进行特别的处理。比如这句话“我不是很喜欢部电影,因为它让我开心不起来。”其中两个形容词“喜欢”、“开心”都是褒义词,但是因为句子的否定句,所以整体是贬义的。有一种比较简单粗暴的处理方式,就是“对否定词(“不”、“非”、“没”等)与句尾标点之间的所有形容词都采用其否定形式”。则这句话中提取出来的形容词就应该是“不喜欢”和“不开心”。
2、 一般说来,最相关的情感词在一些文本片段中仅仅出现一次,词频模型起得作用有限,甚至是负作用,则使用伯努利模型代替多项式模型。这种情况在微博这样的小篇幅文本中似乎不太明显,但是在博客、空间、论坛之类允许长篇幅文本出现的平台中需要注意。
3、其实,副词对情感的评价有一定影响。“不很喜欢”与“很不喜欢”的程度就有很大差异。但如果是朴素贝叶斯方法的话比较难处理这样的情况。我们可以考虑用语言模型或者加入词性标注的信息进行综合判断。这些内容我们将在之后的文章进行探讨。
当然经过以上的处理,情感分析还是会有一部分误判。这里涉及到许多问题,都是情感分析的难点:
1、情绪表达的含蓄微妙:“导演你出来,我保证不打死你。”你让机器怎么判断是褒还是贬?
2、转折性表达:“我非常喜欢这些大牌演员,非常崇拜这个导演,非常赞赏这个剧本,非常欣赏他们的预告片,我甚至为了这部影片整整期待了一年,最后进了电影院发现这是个噩梦。” 五个褒义的形容词、副词对一个不那么贬义的词。机器自然判断成褒义,但这句话是妥妥的贬义。
(2)、拼写纠错
拼写纠错本质上也是一个分类问题。但按照错误类型不同,又分为两种情况:
非词错误(Non-word Errors):指那些拼写错误后的词本身就不合法,如将“wifi”写成“wify”;
真词错误(Real-word Errors):指那些拼写错误后的词仍然是合法的情况,如将“wifi”写成“wife”。
真词错误复杂一些,我们将在接下来的文章中进行探讨。而对于非词错误,就可以直接采用贝叶斯方法,其基本思路如下:
标签:通过计算错误词语的最小编辑距离(之前咱们提到过的),获取最相似的候选词,每个候选词作为一个分类。
特征:拼写错误的词本身。因为它就一个特征,所以没有什么条件独立性假设、朴素贝叶斯啥的。它就是纯而又纯的贝叶斯方法。
判别公式:
训练样本1:该场景下的正常用词语料库,用于计算 P(候选词i)。
训练样本2:该场景下错误词与正确词对应关系的语料库,用于计算 P(错误词|候选词i)
由于自然语言的特点,有一些小技巧需要注意:
1、 据统计,80%的拼写错误编辑距离为1,几乎所有的拼写错误编辑距离小于等于2。我们只选择编辑距离为1或2的词作为候选词,这样就可以减少大量不必要的计算。
2、由于我们只选择编辑距离为1或2的词,其差别只是一两个字母级别差别。因此计算似然函数的时候,可以只统计字母层面的编辑错误,这样搜集的样本更多,更满足大数定律,也更简单。对于编辑距离为1的似然函数计算公式可以进化为:
当然,朴素贝叶斯也是有缺陷的。比如我们知道朴素贝叶斯的局限性来源于其条件独立假设,它将文本看成是词袋子模型,不考虑词语之间的顺序信息,例如:朴素贝叶斯会把“武松打死了老虎”与“老虎打死了武松”认作是一个意思。那么有没有一种方法提高其对词语顺序的识别能力呢?当然有,就是这里要提到的N-gram语言模型。接下来详细给大家介绍N-gram语言模型。
三、N-gram语言模型
1、从假设性独立到联合概率链规则
与我们之前我们垃圾邮件识别中的条件独立假设是一样的:
为了简化起见,我们以字母 xi表示每一个词语,并且先不考虑条件“S”。于是上式就变成了下面的独立性公式。
上面的公式要求满足独立性假设,如果去掉独立性假设,我们应该有下面这个恒等式,即联合概率链规则(chain rule) :
2、从联合概率链规则到n-gram语言模型
上面的联合概率链规则公式考虑到词和词之间的依赖关系,但是比较复杂,在实际生活中几乎没办法使用,于是我们就想了很多办法去近似这个公式,比如我们要讲到的语言模型n-gram就是它的一个简化。如果我们考虑一个词语对上一个词语的依赖关系,公式就简化了如下形式,我们把它叫做二元语法(bigram,2-gram):
如果我们再考虑长一点,考虑n个词语之间的关系,这就是n-gram的由来。其实以上几个简化后的公式,就是著名的马尔科夫假设(Markov Assumption):下一个词的出现仅依赖于它前面的一个或几个词。这相对于联合概率链规则,其实是一个有点粗糙的简化,不过很好地体现了就近思路,离得较远和关系比较弱的词语就被简化和省略了。实际应用中,这些简化后的n-gram语法比独立性假设还是强很多的。
3、怎样选择依赖词的个数"n"?
选择依赖词的个数"n"主要与计算条件概率有关。理论上,只要有足够大的语料,n越大越好,毕竟这样考虑的信息更多嘛。条件概率很好算,统计一下各个元组出现的次数就可以,比如:
但我们实际情况往往是训练语料很有限,很容易产生数据稀疏,不满足大数定律,算出来的概率失真。比如(“发票”,“点数”,“优惠”)在训练集中竟没有出现,就会导致零概率问题。又比如在英文语料库IBM, Brown中,三四百兆的语料,其测试语料14.7%的trigram和2.2%的bigram在训练语料中竟未出现!另一方面,如果n很大,参数空间过大,也无法实用。假设词表的大小为 100,000,那么n-gram模型的参数数量为 100,000n。这么多的参数,估计内存就不够放了。那么,如何选择依赖词的个数n呢?从前人的经验来看:
1、经验上,trigram用的最多。尽管如此,原则上,能用bigram解决,绝不使用trigram。n取≥4的情况较少。
2、更大的n:对下一个词出现的约束信息更多,具有更大的辨别力;
3、更小的n:在训练语料库中出现的次数更多,具有更可靠的统计信息,具有更高的可靠性、实用性。
4、N-gram实际应用举例
(1)、词性标注
词性标注是一个典型的多分类问题。常见的词性包括名词、动词、形容词、副词等。而一个词可能属于多种词性。如“爱”,可能是动词,可能是形容词,也可能是名词。但是一般来说,“爱”作为动词还是比较常见的。所以统一给“爱”分配为动词准确率也还足够高。这种最简单粗暴的思想非常好实现,如果准确率要求不高则也比较常用。它只需要基于词性标注语料库做一个统计就够了,连贝叶斯方法、最大似然法都不要用。词性标注语料库一般是由专业人员搜集好了的,长下面这个样子。其中斜线后面的字母表示一种词性,词性越多说明语料库分得越细;需要比较以下各概率的大小,选择概率最大的词性即可:
但这种方法没有考虑上下文的信息。而一般来说,形容词后面接名词居多,而不接动词,副词后面才接动词,而不接名词。 考虑到词性会受前面一两个词的词性的影响,可以引入2-gram模型提升匹配的精确度。 我们匹配以下这句话(已被空格分好词)中“爱”的词性:
“真诚的 学王玉 很 爱 共产党”
将公式进行以下改造,比较各概率的大小,选择概率最大的词性:
(2)、垃圾邮件识别
1、先对邮件文本进行断句,以句尾标点符号(“。” “!” “?”等)为分隔符将邮件内容拆分成不同的句子。
2、用N-gram分类器(马上提到)判断每个句子是否为垃圾邮件中的敏感句子。
3、当被判断为敏感句子的数量超过一定数量(比如3个)的时候,认为整个邮件就是垃圾邮件。
N-gram分类器是结合贝叶斯方法和语言模型的分类器。这里用 Y1,Y2分别表示这垃圾邮件和正常邮件,用 X表示被判断的邮件的句子。根据贝叶斯公式有:
P(Yi|X)∝P(X|Yi)P(Yi);i=1,2
比较i=1和2时两个概率值的大小即可得到 X所属的分类。对于句子(“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)用字母 X 代表,每一个词语用字母 xi 表示。 X就可以写成一个 xi组成的向量, xi就是这向量中某个维度的特征。对 P(X|Yi)套用2-gram模型。 则上式化简为:
公式中的条件概率也比较好求,举个例子:
剩下的就需要在语料库中间做一个的统计就是了。因为这种方法考虑到了词语前面的一个词语的信息,同时也考虑到了部分语序信息,因此区分效果会比单纯用朴素贝叶斯方法更好。多提几句,N-gram方法在实际应用中有一些tricks需要注意:
3-gram方法的公式与上面类似。此处省略。从区分度来看,3-gram方法更好些。
句子开头的词,比如本例中的“我”,因为要考虑其本身作为开头的特征,可以考虑在其前面再添加一个句子起始符号如"《S》",这样我们就不必单独计算 P(“我”|Yi),而是替换为计算 P(“我”|"《S》",Yi) 。形式上与2-gram统一。 这样统计和预测起来都比较方便。
一般地,如果采用N-gram模型,可以在文本开头加入n-1个虚拟的开始符号,这样在所有情况下预测下一个词的可依赖词数都是一致的。与朴素贝叶斯方法一样,N-gram模型也会发生零概率问题,也需要平滑技术。
(3)、中文分词
之前说过,中文分词技术是“中文NLP中,最最最重要的技术之一”,重要到某搜索引擎厂有专门的team在集中精力优化这一项工作,重要到能影响双语翻译10%的准确度,能影响某些query下搜索引擎几分之一的广告收入。不过简单的分词实现方式中,包含的原理其实也非常易懂。说起来,中文分词也可以理解成一个多分类的问题。 这里用 X表示被分词的句子“我司可办理正规发票”, 用 Yi 表示该句子的一个分词方案。咱们继续套用贝叶斯公式:
P(Yi|X)∝P(X|Yi)P(Yi);i=1,2,3…
比较这些概率的大小,找出使得 P(Yi|X)最大的 Yi即可得到 X 所属的分类(分词方案)了。Yi作为分词方案,其实就是个词串,比如(“我司”,“可”,“办理”,“正规发票”)(“我”,“司可办”,“理正规”,“发票”),也就是一个向量了。而上面贝叶斯公式中 P(X|Yi)项的意思就是在分类方案 Yi的前提下,其对应句子为 X的概率。而无论分词方案是(“我司”,“可”,“办理”,“正规发票”)还是(“我”,“司可办”,“理正规”,“发票”),或者其他什么方案,其对应的句子都是“我司可办理正规发票”。也就是说任意假想的一种分词方式之下生成的句子总是唯一的(只需把分词之间的分界符号扔掉剩下的内容都一样)。于是可以将 P(X|Yi)看作是恒等于1的。这样贝叶斯公式又进一步化简成为:
P(Yi|X)∝P(Yi);i=1,2,3…
也就是说我们只要取最大化的 P(Yi)就成了。而 Yi就是一个词串,也就是一个向量,可以直接套用我们上面的N-gram语言模型。这里采用2-gram。于是有:
P(Y1)=P(“我司”,“可”,“办理”,“正规发票”)=P(“我司”)P(“可”|“我司”)P(“办理”|“可”)P(“正规发票”|“办理”)
第二种分词方案的概率为:
P(Y2)=P(“我”,“司可办”,“理正规”,“发票”)=P(“我”)P(“司可办”|“我”)P(“理正规”|“司可办”)P(“发票”|“理正规”)
由于在语料库中“司可办”与“理正规”一起连续出现的概率为0,于是 P(Y2)=0, P(Y1)的概率更高,优先选择 Y1的分词方案。
(4)、机器翻译与语音识别
除了上述说到的应用,N-gram语言模型在机器翻译和语音识别等顶级NLP应用中也有很大的用途。 当然,机器翻译和语音识别是非常复杂的过程,N-gram语言模型只是其中的一部分,但是缺少它整个过程却进行不下去。对于这两个应用我们不打算罗列大量的公式,而只是举些例子,让大家了解一下语言模型是怎么发挥作用的。 对于机器翻译而言,比如中译英,我们对于同一句话『李雷出现在电视上』,得到的三个译文:
LiLei appeared in TV
In LiLei appeared TV
LiLei appeared on TV
其对应短语的翻译概率是一致的,从短语翻译的角度我们无法评定哪句才是正确的翻译结果。这时候,如果我们再使用语言模型(比如机器翻译里面最常见的是3-gram),我们计算会得到最后一句话:
对应到语音识别问题中,我们也会遇到相同的问题,对于以下的2个句子:
I went to a party
Eye went two a bar tea
或者对应下述2个句子:
你现在在干什么?
你西安载感什么?
其对应的发音是完全一致的,这时如果我们借助于语言模型,我们会发现
上面只是简单的举例,但是大家应该看出来了,在机器翻译和语音识别中,N-gram语言模型有着至关重要的地位。同样在现在最顶级的计算机视觉任务『图片内容表述』中,语言模型也发挥着至关重要的作用。语言模型的重要性可见一斑。
5、平滑技术
现在我们可以比较专门探讨平滑技术了。为了解决零概率问题呢,我们需要给 “未出现的n-gram条件概率分布一个非零估计值,相应得需要降低已出现n-gram条件概率分布,且经数据平滑后一定保证概率和为1”。这就是平滑技术的基本思想。
(1)、拉普拉斯平滑
这是最古老的一种平滑方法,又称加一平滑法,其保证每个n-gram在训练语料中至少出现1次。以计算概率 P(“优惠”|“发票”,“点数”) 为例,公式如下:
在所有不重复的三元组的个数远大于(“发票”,“点数”)出现的次数时,即训练语料库中绝大部分n-gram都是未出现的情况(一般都是如此),效果不佳。
(2)、古德图灵(Good Turing)平滑
通过对语料库的统计,我们能够知道出现 r次 (r>0)的n元组的个数为 Nr。 可以令从未出现的n元组的个数为 N0 。古德图灵平滑的思想是:
出现0次的n元组也不能认为其是0次,应该给它一个比较小的估计值,比如为 d0次。
为了保证总共的(出现和未出现的)n元组的次数不变,其他所有已出现的n元组的次数r应该打一个折扣,比如为 dr 次。
然后再用新的 dr去计算各个条件概率。
所以问题的关键是计算 dr。为了保证平滑前后n元组的总共出现次数不变,有:
所以干脆令:
dr×Nr=(r+1)×Nr+1;r=0,1,2…
这样就可以求出 dr了。但是,当 Nr>Nr+1 时,使得模型质量变差。直接的改进策略就是 “对出现次数超过某个阈值的n元组,不进行平滑,阈值一般取8~10”。
(3)、组合估计平滑
不管是拉普拉斯平滑,还是古德图灵平滑技术,对于未出现的n元组都一视同仁,而这难免存在不合理。 因为哪怕是未发生的事件,相互之间真实的概率也会存在差别。另一方面,一个n元组可能未出现,但是其(n-1)元组或者(n-2)元组是出现过的,这些信息如果不利用就直接浪费掉了。在没有足够的数据对高元n-gram模型进行概率估计时,低元n-gram模型通常可以提供有用的信息。 因此可以利用利用低元n-gram模型的信息对高元n-gram模型进行估计:
如果低元n-gram模型的概率本来就很低,那么就给高元n-gram模型一个较低的估计值;
如果低元n-gram模型有一个中等的概率,那么就给高元n-gram模型一个较高的估计值。常用的组合估计算法有线性差值法和Katz回退法。
6、从N-gram谈回贝叶斯方法
聊了这么多N-gram语言模型,我们再回到贝叶斯方法,从实际应用中看看他们的关联。 最原始的用贝叶斯方法进行分类的公式其实非常简单:
P(Yi|X)∝P(X|Yi)P(Yi);i=1,2,3…
具体到不同应用中,它就可以演化出多种玩法:
对于拼写纠错(非词错误) , X是错误的词语, Yi是候选的改正词语,二者都是标量。
对于垃圾邮件识别, X是邮件中的句子, Yi是备选的邮件类别。 X可以处理成向量, Yi 还是标量。
如果对向量 X采用条件独立假设,就是朴素贝叶斯方法。
如果对向量 X采用马尔科夫假设,就是N-gram语言模型。
对于中文分词, X是被分词的句子, Yi是备选的分词方案(词串)。这里把 X看成是一个整体,所以可以理解成标量。而 Yi则是向量。这里对向量 Yi采用马尔科夫假设,也是N-gram语言模型。
四、贝叶斯的实际应用
首先说明的是,本文的代码和上一篇文章的环境一样,python3.7.5,jupyter notebook。并且要对应的安装好第三方库(numpy、sklearn、jieba等库)。
1、利用贝叶斯进行新闻分类:
下面我们来看一个文本分类问题,经典的新闻主题分类,用朴素贝叶斯怎么做。在实验之前,首先进行数据集准备。我们数据集是Database文件夹(验证码:ozd2):把它放在与代码同一路径下:
另外我们看一下其文件内容以及相应的文本内容:
还有一个就是stop_words的停用词(验证码:kiql)的文本,具体内容如下:
我们的代码使用jupyter notebook编译器,具体的代码如下:
import os
import time
import random
import jieba
import sklearn
from sklearn.naive_bayes import MultinomialNB
import numpy as np
import pylab as pl
import matplotlib.pyplot as plt
def make_word_set(words_file):
words_set = set()
with open(words_file, 'rb') as fp:
for line in fp.readlines():
word = line.strip()
if len(word)>0 and word not in words_set: # 去重
words_set.add(word)
return words_set
def text_processing(folder_path, test_size = 0.2):
folder_list = os.listdir(folder_path)
data_list = []
class_list = []
for folder in folder_list:
new_folder_path = os.path.join(folder_path, folder)
files = os.listdir(new_folder_path)
j = 1
for file in files:
if j > 100:
break
with open(os.path.join(new_folder_path, file), 'rb') as fp:
raw = fp.read()
#jieba.enable_parallel(4)
word_cut = jieba.cut(raw, cut_all=False)
word_list = list(word_cut)
jieba.disable_parallel()
data_list.append(word_list)
class_list.append(folder)
j += 1
data_class_list = list(zip(data_list, class_list))
random.shuffle(data_class_list)
index = int(len(data_class_list)*test_size)+1
train_list = data_class_list[index:]
test_list = data_class_list[:index]
train_data_list, train_class_list = zip(*train_list)
test_data_list, test_class_list = zip(*test_list)
all_words_dict = {}
for word_list in train_data_list:
for word in word_list:
if word in all_words_dict:
all_words_dict[word] += 1
else:
all_words_dict[word] = 1
all_words_tuple_list = sorted(all_words_dict.items(), key = lambda f:f[1], reverse=True)
all_words_list = list(zip(*all_words_tuple_list))[0]
return all_words_list, train_data_list, test_data_list, train_class_list,test_class_list
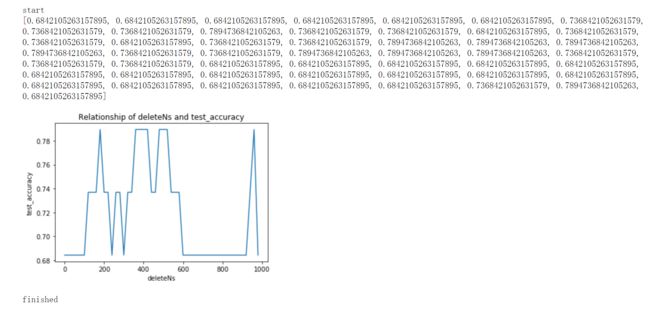
def words_dict(all_words_list, deleteN, stopwords_set = set()):
feature_words = []
n = 1
for t in range(deleteN, len(all_words_list), 1):
if n > 1000:
break
if not all_words_list[t].isdigit() and all_words_list[t] not in stopwords_set and 12、用朴素贝叶斯完成语种检测
其实我们进行另一个项目。试试用朴素贝叶斯完成一个语种检测的分类器,说起来,用朴素贝叶斯完成这个任务,其实准确度还不错。我们这里用的是data数据集(验证码:h7sh)。其数据集如下:
接下来我们将实现的过程详细介绍:
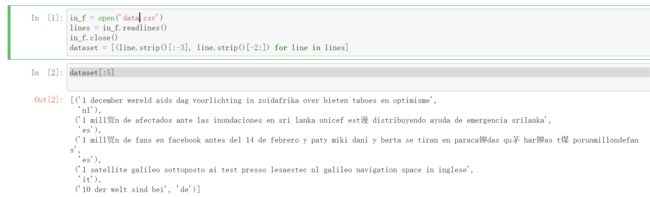
1、首先就是导入数据,查看数据格式:
in_f = open('data.csv')
lines = in_f.readlines()
in_f.close()
dataset = [(line.strip()[:-3], line.strip()[-2:]) for line in lines]
dataset[:5]
2、为了一会儿检测一下咱们的分类器效果怎么样,我们需要一份测试集。所以把原数据集分成训练集的测试集,咱们用sklearn自带的分割函数。
3、模型要有好效果,数据质量要保证。我们用正则表达式,去掉噪声数据。
import re
def remove_noise(document):
noise_pattern = re.compile("|".join(["http\S+", "\@\w+", "\#\w+"]))
clean_text = re.sub(noise_pattern, "", document)
return clean_text.strip()
remove_noise("Trump images are now more popular than cat gifs. @trump #trends http://www.trumptrends.html")
4、下一步要做的就是在降噪数据上抽取出来有用的特征啦,我们抽取1-gram和2-gram的统计特征,然后把分类器import进来并且训练。最后看看我们的准确率如何。
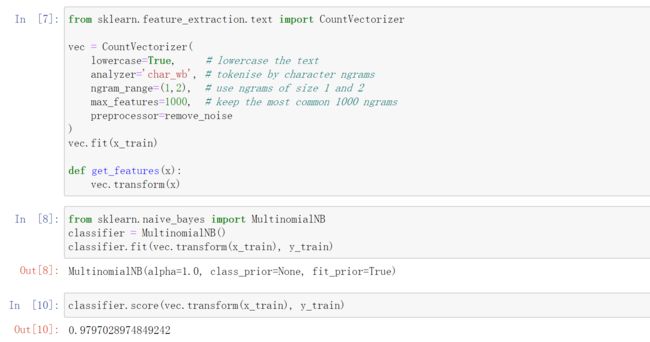
from sklearn.feature_extraction.text import CountVectorizer
vec = CountVectorizer(
lowercase=True, # lowercase the text
analyzer='char_wb', # tokenise by character ngrams
ngram_range=(1,2), # use ngrams of size 1 and 2
max_features=1000, # keep the most common 1000 ngrams
preprocessor=remove_noise
)
vec.fit(x_train)
def get_features(x):
vec.transform(x)
from sklearn.naive_bayes import MultinomialNB
classifier = MultinomialNB()
classifier.fit(vec.transform(x_train), y_train)
classifier.score(vec.transform(x_train), y_train)
能在1500句话上,训练得到准确率97.7%的分类器,效果还是不错的。如果大家加大语料,准确率会非常高。
5、最后,规范化,写成一个class。
import re
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
class LanguageDetector():
def __init__(self, classifier=MultinomialNB()):
self.classifier = classifier
self.vectorizer = CountVectorizer(ngram_range=(1,2), max_features=1000, preprocessor=self._remove_noise)
def _remove_noise(self, document):
noise_pattern = re.compile("|".join(["http\S+", "\@\w+", "\#\w+"]))
clean_text = re.sub(noise_pattern, "", document)
return clean_text
def features(self, X):
return self.vectorizer.transform(X)
def fit(self, X, y):
self.vectorizer.fit(X)
self.classifier.fit(self.features(X), y)
def predict(self, x):
return self.classifier.predict(self.features([x]))
def score(self, X, y):
return self.classifier.score(self.features(X), y)
in_f = open('data.csv')
lines = in_f.readlines()
in_f.close()
dataset = [(line.strip()[:-3], line.strip()[-2:]) for line in lines]
x, y = zip(*dataset)
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1)
language_detector = LanguageDetector()
language_detector.fit(x_train, y_train)
print(language_detector.predict('This is an English sentence'))
print(language_detector.score(x_test, y_test))
这就是我们这个项目的代码,感觉其效果还是不错的。
总结
本文给大家详细的介绍了朴素贝叶斯,这种算法是我们在自然语言处理中最为常用的算法。需要我们掌握其原理以及公式推导。并且本文通过两个案例让大家更好的去理解朴素贝叶斯在文本分类中的应用。并且还指出朴素贝叶斯的缺陷,又为大家介绍了N-gram模型。这也是自然语言处理中较为重要的模型,因此,需要我们认真去掌握以及消化。建议大家最好将案例在自己的电脑上跑一遍,加深对其原理的理解。