2022-02-06每日刷题打卡

2022-02-06每日刷题打卡

1748. 唯一元素的和

给你一个整数数组 nums 。数组中唯一元素是那些只出现 恰好一次 的元素。

请你返回 nums 中唯一元素的 和 。

示例 1：

输入：nums = [1,2,3,2]
输出：4
解释：唯一元素为 [1,3] ，和为 4 。

哈希表记录每个元素的出现次数，再遍历哈希表把出现次数为1的数加起来。

class Solution {
public:
    int sumOfUnique(vector& nums) {
        unordered_mapmymap;
        int sum=0;
        for(auto i:nums)
        {
            mymap[i]++;
        }
        for(auto i:mymap)
            if(i.second<2)sum+=i.first;
        return sum;
    }
};

6000. 对奇偶下标分别排序

给你一个下标从 0 开始的整数数组 nums 。根据下述规则重排 nums 中的值：

按 非递增 顺序排列 nums 奇数下标 上的所有值。
举个例子，如果排序前 nums = [4,1,2,3] ，对奇数下标的值排序后变为 [4,3,2,1] 。奇数下标 1 和 3 的值按照非递增顺序重排。
按 非递减 顺序排列 nums 偶数下标 上的所有值。
举个例子，如果排序前 nums = [4,1,2,3] ，对偶数下标的值排序后变为 [2,1,4,3] 。偶数下标 0 和 2 的值按照非递减顺序重排。
返回重排 nums 的值之后形成的数组。

示例 1：

输入：nums = [4,1,2,3]
输出：[2,3,4,1]
解释：
首先，按非递增顺序重排奇数下标（1 和 3）的值。
所以，nums 从 [4,1,2,3] 变为 [4,3,2,1] 。
然后，按非递减顺序重排偶数下标（0 和 2）的值。
所以，nums 从 [4,1,2,3] 变为 [2,3,4,1] 。
因此，重排之后形成的数组是 [2,3,4,1] 。

准备两个数组，一个存奇数位的，一个存偶数位的。然后遍历nums把数都存入这两个数组里，对奇数位数组递减排序，对偶数位数组递增排序，再把这两个数组合并起来。

class Solution {
public:
    static bool cmp(int a,int b)
    {
        return a>b;
    }
    vector sortEvenOdd(vector& nums) {
        vectorji,ou;
        int n=nums.size();
        for(int i=0;i

6001. 重排数字的最小值

给你一个整数 num 。重排 num 中的各位数字，使其值 最小化 且不含 任何 前导零。

返回不含前导零且值最小的重排数字。

注意，重排各位数字后，num 的符号不会改变。

示例 1：

输入：num = 310
输出：103
解释：310 中各位数字的可行排列有：013、031、103、130、301、310 。
不含任何前导零且值最小的重排数字是 103 。

先判断一下数字是正数还是负数，然后把数字转换成字符串后，对字符串排序，如果数字是正数，就递增排序，反之是递减。要注意的是，递增排序可能出现前缀0，但数字不能有前缀0，所以如果第一个元素是‘0’，就要遍历前面的字符，当遇到第一个非0字符时，交换两个字符。最后再把字符串转换回数字并返回（这里不知道为什么用stol会报错，而且报错消息也很诡异看不明白，所以自己写了一个字符串转化数字的函数，过了）。

class Solution {
public:
    static bool cmp(const char& a,const char& b)
    {
        return a>b;
    }
    long long mystol(string str)
    {
        long long ans=0;
        for(auto i:str)
        {
            ans*=10;
            ans+=i-'0';
        }
        return ans;
    }
    long long smallestNumber(long long num) {
        if(num==0)return 0;
        int ans=1;
        if(num<0)
        {
            ans=-1;
            num*=-1;
        }
        string str=to_string(num);
        if(ans==-1)sort(str.begin(),str.end(),cmp);
        else sort(str.begin(),str.end());
        int n=str.size(),l=0;
        if(str[0]=='0')
        {
            while(str[l]=='0')l++;
            if(l!=0)
            {
                swap(str[l],str[0]);
            }
        }
        long long res=mystol(str);
        return res*ans;
    }
};

6002. 设计位集

位集 Bitset 是一种能以紧凑形式存储位的数据结构。

请你实现 Bitset 类。

Bitset(int size) 用 size 个位初始化 Bitset ，所有位都是 0 。
void fix(int idx) 将下标为 idx 的位上的值更新为 1 。如果值已经是 1 ，则不会发生任何改变。
void unfix(int idx) 将下标为 idx 的位上的值更新为 0 。如果值已经是 0 ，则不会发生任何改变。
void flip() 翻转 Bitset 中每一位上的值。换句话说，所有值为 0 的位将会变成 1 ，反之亦然。
boolean all() 检查 Bitset 中 每一位 的值是否都是 1 。如果满足此条件，返回 true ；否则，返回 false 。
boolean one() 检查 Bitset 中 是否 至少一位 的值是 1 。如果满足此条件，返回 true ；否则，返回 false 。
int count() 返回 Bitset 中值为 1 的位的 总数 。
String toString() 返回 Bitset 的当前组成情况。注意，在结果字符串中，第 i 个下标处的字符应该与 Bitset 中的第 i 位一致。

示例：

输入
[“Bitset”, “fix”, “fix”, “flip”, “all”, “unfix”, “flip”, “one”, “unfix”, “count”, “toString”]
[[5], [3], [1], [], [], [0], [], [], [0], [], []]
输出
[null, null, null, null, false, null, null, true, null, 2, “01010”]

解释
Bitset bs = new Bitset(5); // bitset = “00000”.
bs.fix(3); // 将 idx = 3 处的值更新为 1 ，此时 bitset = “00010” 。
bs.fix(1); // 将 idx = 1 处的值更新为 1 ，此时 bitset = “01010” 。
bs.flip(); // 翻转每一位上的值，此时 bitset = “10101” 。
bs.all(); // 返回 False ，bitset 中的值不全为 1 。
bs.unfix(0); // 将 idx = 0 处的值更新为 0 ，此时 bitset = “00101” 。
bs.flip(); // 翻转每一位上的值，此时 bitset = “11010” 。
bs.one(); // 返回 True ，至少存在一位的值为 1 。
bs.unfix(0); // 将 idx = 0 处的值更新为 0 ，此时 bitset = “01010” 。
bs.count(); // 返回 2 ，当前有 2 位的值为 1 。
bs.toString(); // 返回 “01010” ，即 bitset 的当前组成情况。

不会吧不会吧不会真有人傻乎乎去一位位的翻转吧（欠打）。

这题最大的问题就在翻转上了，因为toString它只调用5次，所以哪怕Bitset的最大长度是2*10^5也不用担心会超时。

解法：

用的是数组模拟Bitset。除此之外还要准备一个记录0个数的计数器zero_num和记录1个数的计数器one_num和一个状态器flag。

先说容易实现的函数：

Bitset(int size)：用size来给数组v开辟空间即可，然后因为各个位置上都是0，所以0的个数就是size，1的个数是0。

boolean all()：判断一下zero_num是否为0，如果为0那肯定全是1了返回true；如果不为0那就返回false。

boolean one()：判断一下one_num是否为0，如果为0就说明一个1没有返回false，反之返回true。

int count()：直接返回one_num即可。

然后说一下翻转问题，因为后面的函数都是和这里有关：

虽然题目说要我们把每一位的元素变换一下，但其实我们不用真的去遍历一遍数组然后一步步去变换，我们可以用准备的flag来记录我们当前的情况（我写的时候用的是int，但啥数据都可以，字符都可以，只要能和另一个状态区分）。当我们调用 flip() 函数时，就把状态翻转过来，我这里flag初始化是1，翻转后我把它变成-1（如果翻转时它是-1那就把它变成1），这样就算完成一个状态的转变，同时还要交换一下zero_num和one_num，毕竟反转了吗，原来有多少0反转后就是多少1，反之一样。如此 filp() 函数就算完成了。

此时你可能有些不明白，为什么这样就算翻转了，待我细细说：

我们大多数时候是不需要知道具体的数组内部是什么样的，只有 fix() , unfix() 和 toString() 这三个函数需要我们知道数组内部的具体数值。那我们在读取数组的时候可以给它加上一层 “滤镜” 本来数组这个位置是0，但我们透过 “滤镜” 看到的它是1 ，也可以修改滤镜的作用，让数组里面是什么我们就看到什么。这个滤镜就是我们记录状态的flag。

void fix() 函数:我们先判断一下flag的状态再做操作：如果我们当前状态已经是翻转后了的，那数组里是0的话，就把它当作1，如果是1的话就当作0；如果没翻转就不做修改。

同理unfix（） 函数也是如此。

string toString() :也是要先判断flag的状态，如果是翻转状态，那数组里是0时我们给字符串接上1，反之接上0；如果不是翻转状态就不做多余操作。剩下的就是遍历数组，把数都转换成字符串存下来最后返回。

class Bitset {
public:
    int zero_num = 0, one_num = 0, flag = 1;
    vectorv;
    Bitset(int size) {
        zero_num = size;
        vectorv1(size, 0);
        swap(v, v1);
    }

    void fix(int idx) {
        if (flag == -1)
        {
            if (v[idx] == 1)
            {
                v[idx] = 0;
                zero_num--;
                one_num++;
            }
        }
        else
        {
            if (v[idx] == 0)
            {
                v[idx] = 1;
                zero_num--;
                one_num++;
            }
        }
    }

    void unfix(int idx) {
        if (flag == -1)
        {
            if (v[idx] == 0)
            {
                v[idx] = 1;
                zero_num++;
                one_num--;
            }
        }
        else
        {
            if (v[idx] == 1)
            {
                v[idx] = 0;
                zero_num++;
                one_num--;
            }
        }
    }

    void flip() {
        flag *= -1;
        swap(zero_num, one_num);
    }

    bool all() {
        if (zero_num == 0)return true;
        return false;
    }

    bool one() {
        if (one_num != 0)return true;
        return false;
    }

    int count() {
        return one_num;
    }

    string toString() {
        string str;
        if (flag == -1)
        {
            for (auto i : v)
            {
                if (i == 1)i = 0;
                else if (i == 0)i = 1;
                str += i + '0';
            }
            return str;
        }
        for (auto i : v)
        {
            str += i + '0';
        }
        return str;
    }
};

/**
 * Your Bitset object will be instantiated and called as such:
 * Bitset* obj = new Bitset(size);
 * obj->fix(idx);
 * obj->unfix(idx);
 * obj->flip();
 * bool param_4 = obj->all();
 * bool param_5 = obj->one();
 * int param_6 = obj->count();
 * string param_7 = obj->toString();
 */

5984. 拆分数位后四位数字的最小和

给你一个四位 正 整数 num 。请你使用 num 中的 数位 ，将 num 拆成两个新的整数 new1 和 new2 。new1 和 new2 中可以有 前导 0 ，且 num 中 所有 数位都必须使用。

比方说，给你 num = 2932 ，你拥有的数位包括：两个 2 ，一个 9 和一个 3 。一些可能的 [new1, new2] 数对为 [22, 93]，[23, 92]，[223, 9] 和 [2, 329] 。
请你返回可以得到的 new1 和 new2 的 最小 和。

示例 1：

输入：num = 2932
输出：52
解释：可行的 [new1, new2] 数对为 [29, 23] ，[223, 9] 等等。
最小和为数对 [29, 23] 的和：29 + 23 = 52 。

蠢比写法，既然这只有4位数要我们分，那就枚举出所有22分开的可能性，对分开的数各位排序后加在一起，然后从中取最小的。为什么不算1 3，因为既然要最小的，那都三位数了肯定不对，题目中13分是因为有0的存在，排序后0变成前缀0被消掉，这里的话对于22分也是一样的。

22分的三种可能性：第一位数和第二位数组合+第三位数和第四位数组合、第一位数和第三位数组合+第二位数和第四位数组合、第一位数和第四位数组合+第二位数和第三位数组合。

class Solution {
public:
    int minimumSum(int num) {
        string str=to_string(num);
        
            
            string s1,s2,s4,s3,s5,s6;
            s1+=str[0];
            s1+=str[1];
            sort(s1.begin(),s1.end());
            s2+=str[2];
            s2+=str[3];
            sort(s2.begin(),s2.end());
            s3+=str[0];
            s3+=str[2];
            sort(s3.begin(),s3.end());
            s4+=str[1];
            s4+=str[3];
            sort(s4.begin(),s4.end());
            s5+=str[0];
            s5+=str[3];
            sort(s5.begin(),s5.end());
            s6+=str[1];
            s6+=str[2];
            sort(s6.begin(),s6.end());
            int num1,num2,num3;
            num1=stoi(s1)+stoi(s2);
            num2=stoi(s3)+stoi(s4);
            num3=stoi(s5)+stoi(s6);
            return min(num1,min(num2,num3));
        
    }
};

5985. 根据给定数字划分数组

给你一个下标从 0 开始的整数数组 nums 和一个整数 pivot 。请你将 nums 重新排列，使得以下条件均成立：

所有小于 pivot 的元素都出现在所有大于 pivot 的元素 之前 。
所有等于 pivot 的元素都出现在小于和大于 pivot 的元素 中间 。
小于 pivot 的元素之间和大于 pivot 的元素之间的 相对顺序 不发生改变。
更正式的，考虑每一对 pi，pj ，pi 是初始时位置 i 元素的新位置，pj 是初始时位置 j 元素的新位置。对于小于 pivot 的元素，如果 i < j 且 nums[i] < pivot 和 nums[j] < pivot 都成立，那么 pi < pj 也成立。类似的，对于大于 pivot 的元素，如果 i < j 且 nums[i] > pivot 和 nums[j] > pivot 都成立，那么 pi < pj 。
请你返回重新排列 nums 数组后的结果数组。

示例 1：

输入：nums = [9,12,5,10,14,3,10], pivot = 10
输出：[9,5,3,10,10,12,14]
解释：
元素 9 ，5 和 3 小于 pivot ，所以它们在数组的最左边。
元素 12 和 14 大于 pivot ，所以它们在数组的最右边。
小于 pivot 的元素的相对位置和大于 pivot 的元素的相对位置分别为 [9, 5, 3] 和 [12, 14] ，它们在结果数组中的相对顺序需要保留。

逆归并排序+归并排序。准备两个数组，一个存大于pivot的，一个存小于pivot的，在准备一个计数器用来计算等于pivot的情况。遍历nums，把数都存入之前准备好的数组里，当遇到等于pivot的数时，计数器++。然后先把小于pivot的数插回nums里，再根据计数器的数量把pivot也插入nums里，最后再把大于pivot数组的数插回nums。（因为题目要求等于pivot的必须是在两者之间，所以我们先插小于pivot的，再插等于pivot的，再插大于pivot的）

class Solution {
public:
    vector pivotArray(vector& nums, int pivot) {
        int n=nums.size(),ans=0,res=0;
        vectorv(n);
        for(int i=0;ipivot)
                v[ans++]=nums[i];
        }
        return v;
    }
};

5986. 设置时间的最少代价

常见的微波炉可以设置加热时间，且加热时间满足以下条件：

至少为 1 秒钟。
至多为 99 分 99 秒。
你可以 最多 输入 4 个数字 来设置加热时间。如果你输入的位数不足 4 位，微波炉会自动加 前缀 0 来补足 4 位。微波炉会将设置好的四位数中，前 两位当作分钟数，后 两位当作秒数。它们所表示的总时间就是加热时间。比方说：

你输入 9 5 4 （三个数字），被自动补足为 0954 ，并表示 9 分 54 秒。
你输入 0 0 0 8 （四个数字），表示 0 分 8 秒。
你输入 8 0 9 0 ，表示 80 分 90 秒。
你输入 8 1 3 0 ，表示 81 分 30 秒。
给你整数 startAt ，moveCost ，pushCost 和 targetSeconds 。一开始，你的手指在数字 startAt 处。将手指移到 任何其他数字 ，需要花费 moveCost 的单位代价。每 输入你手指所在位置的数字一次，需要花费 pushCost 的单位代价。

要设置 targetSeconds 秒的加热时间，可能会有多种设置方法。你想要知道这些方法中，总代价最小为多少。

请你能返回设置 targetSeconds 秒钟加热时间需要花费的最少代价。

请记住，虽然微波炉的秒数最多可以设置到 99 秒，但一分钟等于 60 秒。

输入：startAt = 1, moveCost = 2, pushCost = 1, targetSeconds = 600
输出：6
解释：以下为设置加热时间的所有方法。

• 1 0 0 0 ，表示 10 分 0 秒。
  手指一开始就在数字 1 处，输入 1 （代价为 1），移到 0 处（代价为 2），输入 0（代价为 1），输入 0（代价为 1），输入 0（代价为 1）。
  总代价为：1 + 2 + 1 + 1 + 1 = 6 。这是所有方案中的最小代价。
• 0 9 6 0，表示 9 分 60 秒。它也表示 600 秒。
  手指移到 0 处（代价为 2），输入 0 （代价为 1），移到 9 处（代价为 2），输入 9（代价为 1），移到 6 处（代价为 2），输入 6（代价为 1），移到 0 处（代价为 2），输入 0（代价为 1）。
  总代价为：2 + 1 + 2 + 1 + 2 + 1 + 2 + 1 = 12 。
• 9 6 0，微波炉自动补全为 0960 ，表示 9 分 60 秒。
  手指移到 9 处（代价为 2），输入 9 （代价为 1），移到 6 处（代价为 2），输入 6（代价为 1），移到 0 处（代价为 2），输入 0（代价为 1）。
  总代价为：2 + 1 + 2 + 1 + 2 + 1 = 9 。

这题梦回高中语文阅读理解，光题我就看了半天。

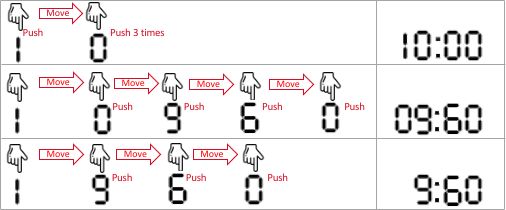
简单来说就是你可以选择输入的方式，每次你输入一个数之后就会跳到下一个数上，这个输入的过程是从左往右，不够四位数时自动补充前缀0，比如你要60秒，那就先输入6再输入0，然后自动补齐前缀0就是0060——00：60。注意的是同一个时间可能有不同表现，比如60秒也可以变成1分钟，即01:00，这题就是让我们求怎么样花费的时间最少。

首先，这里总计也就4位数，所以组合也是有限的，我们把目标时间的所有表示结果都存起来，然后一个个比较输入所花费的时间。我们不用考虑前缀0的花费时间，因为我们也不需要自己输入前缀0，960和0960，肯定是960更方便。

时间大致一共可变成这几种情况：

当目标时间小于99秒时就算一种情况，即只有秒数；如果大于60秒可以转换成分钟的形式，比如150就可以转换成2：30；当转化成分钟后判断秒数部分是否小于等于33，如果满足，可以分钟减一，然后秒数加60，即1：90也是150。

然后就开始模拟输入时间，当要输入一个数时判断当前startAt是否指向我们要输入的数，如果不是就给总时间上加上moveCost，并把startAt变成我们想要的数，再给总时间加上pushCost来输入一个数，如果一开始startAt就是我们要的数，就直接输入即可。

找出最小值并返回。（还有就是要注意，秒数转化分钟时，分钟数最大只能是99，不能是100，如果遇到分钟转化成100的，要自动-1，然后秒数+60。

class Solution {
public:
    int minCostSetTime(int startAt, int moveCost, int pushCost, int targetSeconds) {
    vectorv;
    if(targetSeconds<=99)v.push_back(to_string(targetSeconds));
    int num = targetSeconds / 60;
    targetSeconds %= 60;
    if (num >= 100)
    {
        num--;
        targetSeconds+=60;
    }
    int res = 100*num+targetSeconds;
    v.push_back(to_string(res));
    if (targetSeconds <= 39)v.push_back(to_string(num - 1) + to_string(targetSeconds + 60));
    int min_time = INT_MAX,m= startAt,len=v.size();
    for (int i = 0; i < len; i++)
    {
        int n = v[i].size(), ans = 0;
        for (int j = 0; j < n; j++)
        {
            if (startAt != v[i][j] - '0')
            {
                ans += moveCost;
                startAt = v[i][j] - '0';
            }
            ans += pushCost;
        }
        startAt = m;
        min_time = min(ans, min_time);
    }
    return min_time;
}
};