发自
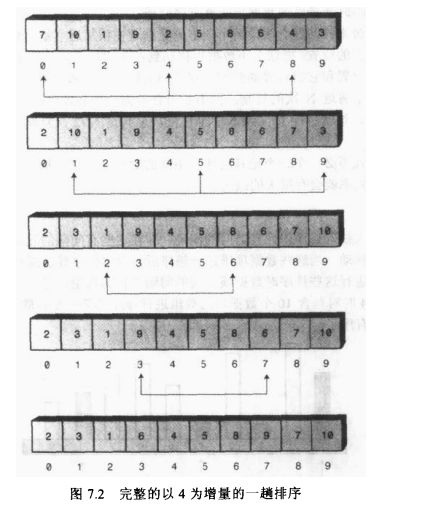
希尔排序
快速排序
划分数据就是把数据分为两组,使所有关键字大于特定值的数据项在一组,使所有关键字小于特定值的数据项在另一组。很容易想像划分数据的情况。比如可以将职员记录分为两组:家住距离办公地点15英里以内的雇员和住在15英里以外的雇员。或者学校管理者想要把学生分成年级平均成绩高于3.5和低于35的两组,以此来判定哪些学生应该在系主任掌握的名单里。
正如大家看到的一样,有三个基本的步骤
1.把数组或者子数组划分成左边(较小的关键字)的一组和右边(较大的关键字)的一组。
2.调用自身对左边的一组进行排序。
3.再次调用自身对右边的一组进行排序。
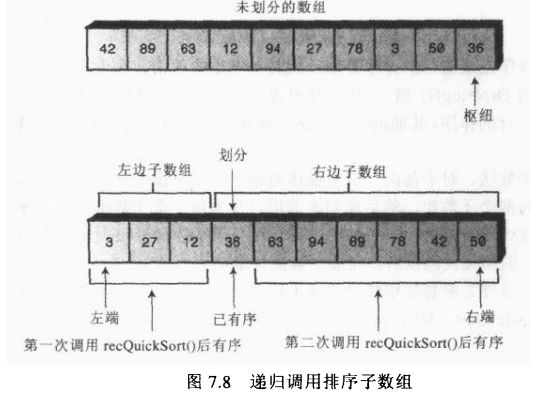
经过一次划分之后,所有在左边子数组的数据项都小于在右边子数组的数据项。只要对左边子数组和右边子数组分别进行排序,整个数组就是有序的了,如何对子数组进行排序呢?通过递归的调用排序算法自身就可以。
传递给 recQuick Sort(方法的参数决定了要排序数组(或者子数组)的左右两端的位置。这个方法首先检査数组是否只包含一个数据项。如果数组只包含一个数据项,那么就定义数组已经有序,方法立即返回。这是这个递归过程的基值(终止)条件。
如果数组包含两个或者更多的数据项,算法就调用在前面一节中讲过的 partitionIto方法对这个数组进行划分。方法返回分割边界的下标数值( partition),它指向右边(较大的关键字)子数组最左端的数据项。划分标记给出两个子数组的分界。如图7.8所示。
选择枢纽
partitionlto方法应该使用什么样的枢纽呢?以下是一些相关的思想:
应该选择具体的一个数据项的关键字的值作为枢组;称这个数据项为 pivot(枢纽)。
可以选择任意一个数据项作为枢纽。为了简便,我们假设总是选择待划分的子数组最右端的数据项作为枢纽。
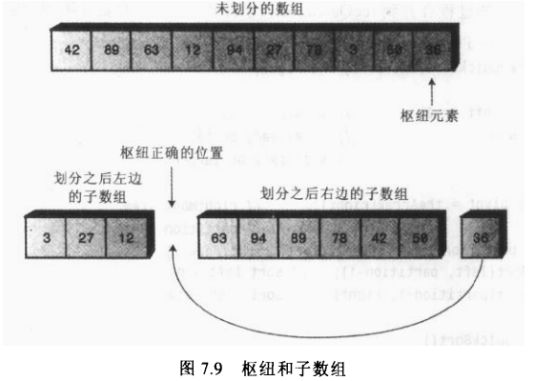
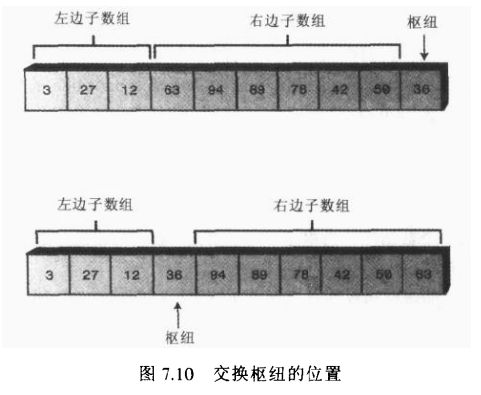
划分完成之后,如果枢纽被插入到左右子数组之间的分界处,那么枢纽就落在排序之后的最终位置上了。
基数排序算法
这里讨论的基数排序都是普通的以10为基数的运算,因为这样更易于讲解。但是,以2为基数实现的基数排序也是非常高效的,这可以利用计算机高速的位运算。这里只考察基数排序,而不考察与基数排序相似但更复杂一些的基数交换排序。基数这个词的意思是一个数字系统的基。10是十进制系统的基数,2是二进制系统的基数。排序包括分别检测关键字的每一个数字,检测从个位最低有效位)开始
1.根据数据项个位上的值,把所有的数据项分为10组。
2然后对这10组数据项重新排列:把所有关键字是以0结尾的数据项排在最前面,然后是关键字结尾是1的数据项,照此顺序直到以9结尾的数据项。这个步骤被称为第一趟子排序。
3.在第二趟子排序中,再次把所有的数据项分为10组,但是这一次是根据数据项十位上的值来分组的。这次分组不能改变先前的排序顺序。也就是说,第二趟排序之后,从每一组数据项的内部来看,数据项的顺序保持不变;这趟子排序必须是稳定的。
4.然后再把10组数据项重新合并,排在最前面的是十位上为0的数据项,然后是10位为1的数据项,如此排序直到十位上为9的数据项。
5.对剩余位重复这个过程。如果某些数据项的位数少于其他数据项,那么认为它们的高位为0。
下面是一个例子,有7个数据項,每个数据项都有三位。为了清晰起见显示第一位的0
小结
希尔排序将增量应用到插入排序,然后逐渐缩小增量。
n-增量排序表示每隔n个元素进行排序。
被称为间隔序列或者间距序列的数列决定了希尔排序的排序间隔。
常用的间隔序列是由递归表达式h=3*h+1生成的,h的初始值为1。
一个容纳了1000个数据项的数组,对它进行希尔排序可以是间隔序列为364,121,40,13,4,最后是1的增量排序。
希尔排序很难分析,但是它运行的时间复杂度大约为O(N(logN)。这比时间复杂度为O(N)的排序算法要快,例如比插入排序快,但是比时间复杂度为O(NlogN)的算法慢,例如比快速排序慢。
划分数组就是把数组分为两个子数组,在一组中所有的数据项关键字的值都小于指定的值,而在另一组中所有数据项关键字的值则大于或等于给定值。
枢纽是在划分的过程中确定数据项应该放在哪一组的值。小于枢纽的数据项都放在左边组;而大于枢纽的数据项都放在右边一组。
在划分算法中,在各自的 while循环中的两个数组下标的指针,分别从数组的两端开始,相向移动,查找需要交换的数据项。
当一个数组下标指针找到一个需要交换的数据项时,它的 while循环中止。
当两个 while循环都终止时,交换这两个数据项。
当两个 while循环都终止时,并且两个子数组的下标指针相遇或者交错,则划分过程结束。
划分操作有线性的时间复杂度ON),做N+1或N+2次的比较以及少于N2次的交换。
划分算法的内部 while循环需要额外的检测,以防止数组下标越界。
快速排序划分一个数组,然后递归调用自身,对划分得到的两个子数组进行快速排序。
只含有一个数据项的子数组定为已经有序,这一点可以作为快速排序算法的基值(终止)条件。
快速排序算法划分时的枢纽是一个特定数据项关键字的值,这个数据项称为 pivot(枢纽)。
在快速排序的简单版本中,总是由子数组的最右端的数据项作为枢纽。
划分的过程中枢纽总是放在被划分子数组的右界,它不包含在划分过程中。
划分之后枢纽也换位,被放在两个划分子数组之间。这就是枢纽的最终排序位置。
快速排序的简单版本,对已经有序(或者逆序)的数据项排序的执行效率只有O(N2)。
更高级的快速排序版本中,枢纽是子数组中第一个、最后一个以及中间一个数据项的中值。这称为“三数据项取中”( median- of-three)划分。
三数据项取中划分有效地解决了对已有序数据项排序时执行效率仅是O(N2)的问题。
在三数据项取中划分中,在对左端、中间以及右端的数据项取中值的同时对它们进行排序。
这个排序算法消除了划分算法内部 while循环中对数据越界的检测。
快速排序算法的时间复杂度为O(N*log2N)(除了用简单的快速排序版本对已有序数据项排序的情况)。
子数组小于一定的容量(切割界限, cutoff时用另一种方法来排序,而不用快速排序。
通常用插入排序对小于切割界限的子数组排序。
在快速排序已经对大于切割界限的子数组排完序之后,插入排序也可用于整个的数组。
基数排序的时间复杂度和快速排序相同,只是它需要两倍的存储空间。