密码学入门(4):公钥密码
密码学入门(4):公钥密码
文章目录
- 密码学入门(4):公钥密码
-
- 密钥配送问题
-
- 解决密钥配送问题的方法
- 公钥密码
- RSA
-
- 生成密钥对
- 对RSA的攻击
- 中间人攻击
- 其他公钥密码
- 混合密码系统
-
- 密码技术的组合
- 参考
公钥密码用公钥加密,私钥解密。
密钥配送问题
在对称密码中,由于加密和解密的密钥都是相同的,因此必须向接收者配送密钥。而在Alice将密钥发送给Bob时,会被Eve窃听,因此Eve就能像Bob一样完成密文的解密。
Alice感到一筹莫展。不发送密钥吧,接收者Bob无法解密;发送密钥吧,连窃听者Eve也可以解密了。密钥必须要发送,但又不能发送,这就是对称密码的密钥配送问题。
解决密钥配送问题的方法
- 通过事先共享密钥来解决:这是最简单的一种解决方法,就是事先用安全的方式将密钥交给对方,这称为密钥的事先共享。
- 问题:假设一个公司有 1000 1000 1000名员工需要彼此加密通信,因此每个人需要 999 999 999个通信密钥。所以整个公司需要的密钥数量为 1000 × 999 ÷ 2 = 499500 1000 \times 999 \div 2 = 499500 1000×999÷2=499500。全公司要生成 49 49 49万 9500 9500 9500个密钥,这是不现实的。
- 通过密钥分配中心来解决:在公司中配置一台充当密钥分配中心的计算机,其中保存了公司中每个员工的密钥。当Alice要与Bob通信时:
- Alice向密钥分配中心发出希望与Bob进行通信的请求。
- 密钥分配中心随机生成一个会话密钥,是本次通信中的临时密钥。
- 密钥分配中心将会话密钥分别加密后发送给Alice和Bob(密钥分配中心有Alice和Bob的密钥)。
- Alice得到会话密钥后,用它对消息进行加密,然后发送给Bob。
- Bob得到会话密钥后,用它对消息进行解密,得到Alice发送的消息原文。
- Alice和Bob删除会话密钥。
- 问题
- 随着员工数量的增加,密钥分配中心的负荷也回随之增加。
- 密钥分配中心如果发生故障,全公司的加密通信就会瘫痪。
- 主动攻击者Mallory可以直接对密钥分配中心下手。
- 通过Diffie-Hellman密钥交换来解决:在Diffie-Hellman密钥交换中,进行加密通信的双方需要交换一些信息,根据所交换的信息,双方可以各自生成相同的密钥。而这些信息即使被窃听者Eve窃听到,也无法生成相同的密钥。
- 通过公钥密码解决:公钥密码中加密密钥和解密密钥是不同的。接收者只需要事先将加密密钥发送给发送方,这个加密密钥即使被窃听者获取也没有问题。发送者使用加密密钥对通信内容进行加密并发送给接受者,而只有拥有解密密钥的人(即接收者本人)才能进行解密。
公钥密码
公钥密码(public-key cryptography)中,密钥分为加密密钥和解密密钥。发送者用加密密钥对消息进行加密,接收者用解密密钥对密文进行解密。
加密密钥和解密密钥的区别:
- 发送者只需要加密密钥。
- 接收者只需要解密密钥。
- 解密密钥不可以被窃听者获取。
- 加密密钥被窃听者获取也没问题。
由于加密密钥可以任意公开,因此该密钥被称为公钥(public key)。而解密密钥时绝对不能公开的,因此称为私钥(private key)。公钥和私钥是一一对应的,一对公钥和私钥统称为密钥对(key pair)。
公钥通信的流程:
在这个过程中,Alice和Bob之间传输的信息只有Bob的公钥和用Bob的公钥加密的密文。由于Bob的私钥没有出现在通信内容中,因此窃听者Eve无法对密文进行解密。
公钥密码无法解决的问题:
- 会受到中间人攻击。
- 处理速度慢,只有对成密码的几百分之一。
公钥密码除了能保证数据传输的机密性,还能用作数字签名,提供认证功能。例如,假设现在Alice希望把一个数字签署的信息 M ′ M' M′发送给Bob,那么:
- Alice可以用私钥加密信息 M ′ M' M′,得到数字签名 σ \sigma σ。
- Alice把消息/签名对 ( M ′ , σ ) (M', \sigma) (M′,σ)发送给Bob。
- Bob收到 ( M ′ , σ ) (M', \sigma) (M′,σ)后,他可以利用Alice的公钥解密 σ \sigma σ,如果解密后的数据与 M ′ M' M′相同,就能证实消息确实来自Alice。
RSA
RSA是一种公钥密码算法,它的名字是由它的三位开发者,即Ron Rivest、Adi Shamir和Leonard Adleman的姓氏首字母组成的(Rivest-Shamir-Adleman)。
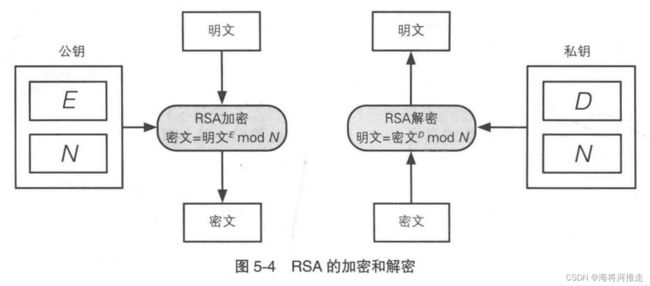
在这里,数 E E E和数 N N N共同组成了公钥 ( E , N ) (E, N) (E,N),数 D D D和数 N N N共同组成了私钥 ( D , N ) (D, N) (D,N)。其中 E E E是加密(Encryption)的首字母, D D D是解密(Decryption)的首字母, N N N是数字(Number)的首字母。同时,被加密的明文需要小于 N N N,否则就要将明文分解。
生成密钥对
那么,如何生成密钥对?通过上面可以知道, E E E和 N N N是公钥, D D D和 N N N是私钥,因此求 E E E、 D D D和 N N N这三个数就是生成密钥对(这里涉及到了一些数学问题,不感兴趣可以跳过):
-
求 N N N:选择两个很大的(例如 1024 1024 1024bit)质数 p p p和 q q q,那么:
N = p × q N = p \times q N=p×q -
求 L L L: L L L这个数在RSA加密和解密中都不出现,它只出现在生成密钥对的过程中。 L L L是 p − 1 p - 1 p−1和 q − 1 q - 1 q−1的最小公倍数(least common multiple,lcm):
L = l c m ( p − 1 , q − 1 ) L = lcm(p - 1, q - 1) L=lcm(p−1,q−1) -
求 E E E: E E E是一个比 1 1 1大、比 L L L小的数,并且 E E E与 L L L互质,即 E E E和 L L L的最大公约数为 1 1 1:
{ 1 < E < L g c d ( E , L ) = 1 \begin{cases} 1 < E < L \\ gcd(E, L) = 1 \end{cases} {1<E<Lgcd(E,L)=1 -
求 D D D:数 D D D是由数 E E E计算得到的。 D D D、 E E E和 L L L之间必须具备下列关系:
{ 1 < D < L E × D m o d L = 1 \begin{cases} 1 < D < L\\ E \times D\, mod\, L = 1 \end{cases} {1<D<LE×DmodL=1
要保证存在满足条件的 D D D,就需要保证 E E E和 L L L的最大公约数为 1 1 1,这也是 ( 3 ) (3) (3)中对 E E E所要求的条件。
这里面可能会有一些疑问,例如:
- 如何选两个很大的质数?
- 我们可以生成一个 1024 1024 1024bit的随机数 n n n,然后判断它是否是质数,如果不是则在 n n n附近随机选取大约 ln n \ln n lnn个整数,并进行质数检验。为什么是 ln n \ln n lnn个整数涉及到了质数的密度,具体可以参考《算法导论》。
- 如何选一个和 L L L互质的数?
- 我们可以在 1 < E < L 1 < E < L 1<E<L内随机选一个数,然后再判断它是否满足 g c d ( E , L ) = 1 gcd(E, L) = 1 gcd(E,L)=1,其中求 g c d gcd gcd可以使用辗转相除法,具体可以参考《算法导论》。
- 如何计算 22 5 29 m o d 323 225^{29} mod 323 22529mod323?
- 这是一个幂取模问题,可以使用反复平方法,具体可以参考《算法导论》。
对RSA的攻击
RSA的安全性主要来源于对大整数进行因式分解的困难性。如果破译者能对公钥中的 E × D m o d L = 1 E \times D\, mod\, L = 1 E×DmodL=1进行分解,就可以根据公钥推导出密钥。要由 E E E计算出 D D D,就需要数字 L L L,因此就需要知道 p p p和 q q q。
如果分解大整数是困难的,那么打破RSA也是困难的。经过20多年的研究,人们还没有发现比分解 E × D m o d L = 1 E \times D\, mod\, L = 1 E×DmodL=1更容易的方法来打破RSA加密系统。事实上,对大整数的分解是相当困难的。通过随机地选取两个 1024 1024 1024bit的质数并求出它们的积,就可以创建出一把无法用现行技术在可行的时间内“破解”的公钥。
中间人攻击
中间人攻击(man-in-the-middle attack)不仅是针对RSA,而是可以针对任何公钥密码。它虽然不能破译公钥密码,但却是一种针对机密性的有效攻击。
所谓中间人攻击,就是主动攻击者Mallory混入发送者和接收者的中间,对发送者伪装成接收者,对接收者伪装成发送者的攻击方式,在这里“Mallory”就是“中间人”。
在这个过程中,公钥密码并没有被破译,所有的密码算法也都正常工作并确保了机密性。然而,所谓的机密性并非在Alice和Bob之间,而是在Alice和Mallory之间,以及Mallory和Bob之间。仅靠公钥密码本身,是无法防御中间人攻击的。
其他公钥密码
- ELGamal方式:RSA利用了质因数分解的困难度,而ELGamal方式则利用了 m o d N mod\, N modN下求离散对数的困难度。但它的缺点是经过加密的密文长度会变成明文的两倍。
- Rabin方式:它利用了 m o d N mod\, N modN下求平方根的困难度。破译Rabin方式公钥密码的困难度与质因数分解的困难的相当。
- 椭圆曲线密码(Elliptic Curve Cryptography,ECC):它是通过将椭圆曲线上的特定点进行特殊的乘法运算来实现的,利用了这种乘法运算的逆运算非常困难的特性。它的特点是所需的密钥长度比RSA短。
混合密码系统
公钥密码可以避免密钥配送问题,但它的处理速度远远低于对称密码。而混合密码系统可以解决对称密码的密钥配送问题,还能解决公钥密码速度慢的问题。
混合密码系统(hybrid cryptosystem)是将对称密码和公钥密码的优势相结合的方法。它用快速的对称密码来对消息进行加密,用公钥密码对加密消息时使用的对称密码的密钥进行加密。由于对称密码的密钥一般比消息本身要短,因此公钥密码速度慢的问题就可以忽略了。
混合密码系统的组成机制:
- 用对称密码加密消息。
- 通过伪随机数生成器生成对称密码加密中使用的会话密钥。
- 用公钥密码加密会话密钥。
- 从混合密码系统外部赋予公钥密码加密时使用的密钥。
混合密码系统的加密:
- 加密消息:消息的加密方式和对称密码的一般加密方法相同。
- 加密会话密钥:会话密钥(session key)是指为本次通信而生成的临时密钥,一般通过伪随机数生成器产生。
- 会话密钥是对称密码的密钥,同时也是公钥密码的明文。
混合密码系统的解密:
密码技术的组合
混合密码系统是将对称密码和公钥密码相结合,从而构建出一种同时发挥两者优势的系统。密码学中还有一些多种技术组合而成的技术,我们先做个简单的介绍:
- 数字签名:由单向散列函数和公钥密码组合而成。
- 证书:由公钥和数字签名组合而成。
- 消息认证码:由单向散列函数和密钥组合而成,也可以通过对称密码来生成。
- 伪随机数生成器:可以使用对称密码、单向散列函数或公钥密码来构建。
参考
- 《图解密码技术》
- 《算法导论》