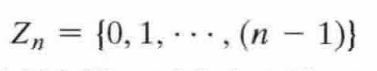密码学中数论和有限域基本概念

毕设学习过程中得学习笔记
参考书是密码编码学与网络安全

---

整除

b整除a，即是a/b没有余数，即为b|a，称b为a的因子

整数整除的性质

①若a|1，则 a = ±1.
②若a|b，且b|a，则 a = ±b。
③任意非零数b整除0.
④若a|b，b|c，则a|c
⑤若b|g，b|h，则对任意整数m，n，有b|(mg+nh)

欧几里得算法

欧几里得算法基于定理：

对于任意非负整数a和任意正整数b，

gcd (a，b) = gcd (b，a mod b)

定义1：两个整数称为互素的，如果它们唯一的正整数公因子是1。

最大公因子：对于整数a和b，能够同时整除a和b的最大整数是a和b的最大公因子，记为gcd(a，b)。定义gcd(0，0) = 0。

因此如果 gcd(a，b) = 1，那么a和b互素。

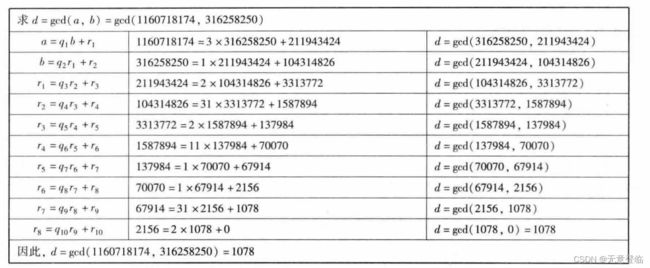
求最大公因子
设有整数a，b，使得 d = gcd(a，b)。因为要求的最大公因子是正整数，所以gcd(a，b)=gcd(|a|，|b|)，因此假设a≥b>0。
现在用b除a，则a= q₁ x b + r₁，0≤r₁ 若r₁=0，则b|a，d=gcd(a，b)=b。
若r₁≠0，由整除性质⑤，d|a，d|b，那么d|(a-q₁ x b)，因此d|r₁。
而对任意整数c，若c|b，c|r₁，那么c|(q₁ x b+r₁)=c|a，又d=gcd(a，b)，则有c≤b，因此d=gcd(b，r₁)。
因为b＞r₁，用r₁除b，则b= q₂ x r₁ + r₂，0≤r₂＜r₁。
和前面一样分为r₂=0和r₂≠0讨论，这样辗转相除直到除法过程中余数为0。

模运算

如果a是整数，n是正整数，则定义a模n是a除以n所得的余数。整数n称为模数。
如果(a mod n) = (b mod n)，则称整数a和b是模n同余的。表示为a≡b(mod n)

同余的性质

①如果n|(a - b)，那么a≡b(mod n)。
②a≡b(mod n)隐含b≡a(mod n)。
③a≡b(mod n)，b≡c(mod n)隐含a≡c(mod n)。

①证明：
如果n|(a - b)，那么存在某个k使得(a-b)=kn。于是有a=b+kn。
因此(a mod n) = (b + kn除以n的余数) = (b除以n的余数) = (b mod n)。

模算术运算

性质：

①[ (a mod n) + (b mod n) ] mod n = (a + b) mod n
②[ (a mod n) - (b mod n) ] mod n = (a - b) mod n
③[ (a mod n) x (b mod n) ] mod n = (a x b) mod n

和普通算术一样，幂运算可通过重复乘法实现

以模8运算为例

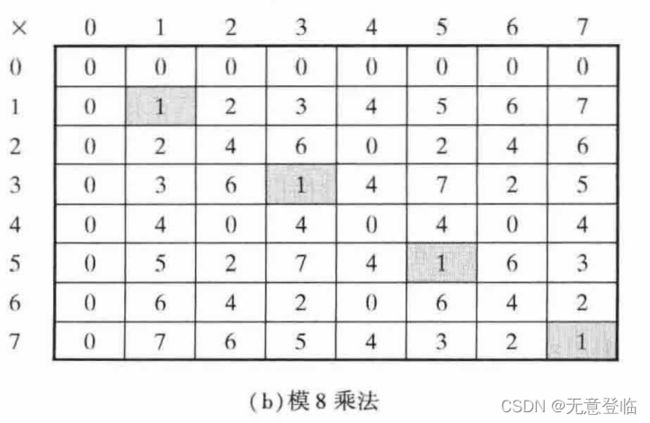
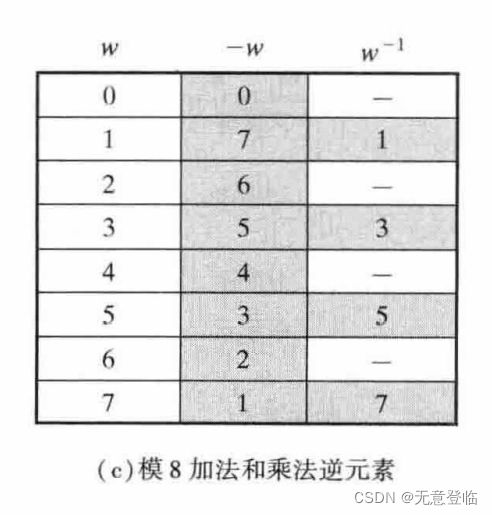
模运算中，整数x的加法逆元素是使(x + y)mod n = 0的y值，乘法逆元素是使(x * y)mod n = 1 mod n的y值

定义：比n小的非负整数集合：

称为剩余类集，或模n的剩余类。

可以将模n的剩余类表示为[0], [1], [2], … , [n-1]，其中[r]={a：a是一个整数，a≡r(mod n)}

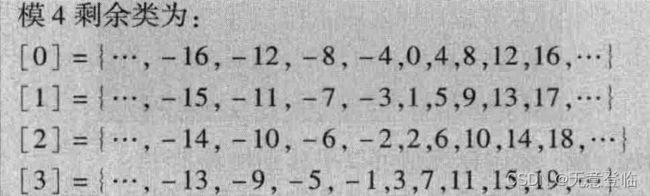
在剩余类的所有整数中，通常用最小非负整数代表这个剩余类。寻找与k是模n同余的最小非负整数的过程，称为模n的k约化。

剩余类集Z_n是有乘法单位元的交换环。

模运算的加法逆元存在性和普通运算是一致的，然而乘法逆元存在性与普通运算有所区别。一般来说，如果一个整数与n互素，那么它在Z_n中有一个乘法逆元。

扩展的欧几里得算法

对于给定的整数a和b，扩展的欧几里得算法不仅计算出最大公因子d，而且还有另外两个整数x和y，满足如下方程：

ax + by = d = gcd (a，b)

x和y有相反的正负号。一般地，可以证明对于两个给定的整数a和b，ax+by的最小正整数等于gcd(a，b)。

群、环、域

群

群G，是定义了一个二元运算的集合，记为{G，·}，G中每一个序偶(a，b)通过运算生成G中的元素(a，b)。
满足以下公理：

①封闭性：如果a和b都属于G，则a·b也属于G。
②结合律：对于G中任意元素a、b、c，都有a·(b·c)=(a·b)·c成立。
③单位元：G中存在一个元素e，对于G中任意元素a，都有a·e=e·a=a成立。
④逆元：对于G中任意元素a，G中都存在一个元素a‘，使得下式成立a·a’=a’·a=e。

如果一个群的元素是有限的，则该群称为有限群。并且群的阶就等于群中元素的个数。否则，称该群为无限群。

一个群若满足以下条件，则成为交换群，也叫阿贝尔群：

⑤交换律：对于G中任意元素a、b，都有a·b=b·a成立。

当群中的运算符是加法时，其单位元是0；a的逆元是-a；并且定义减法为：a-b=a+(-b)。

定义幂运算为重复运用群中的运算，如a³=a·a·a。并且定义a⁰=e作为单位元；a^-n=(a’)ⁿ,其中a’是a在群内的逆元。

循环群： 群中的每一个元素都是一个固定元素a(a∈G)的幂a^k(k为整数)。

元素a生成了群G，或者说a是群G的生成元。
循环群总是交换群，可能是有限群或无限群。

环

环R，记为{R，+，x}，是一个有两个二元运算的集合，对于R中任意元素a、b、c满足以下公理：

R关于加法是一个交换群；因此R满足从上述①-⑤的所有原则。
乘法的封闭性：如果a和b都属于R，则ab也属于R。
乘法的结合律：对于R中任意元素a、b、c，有 a(bc)=(ab)c成立。
分配律：对于R中的任意元素a、b、c，下面两个式子总成立 a (b+c) = ab + ac; (a+b) c = ac + bc

实数上所有n阶方阵的集合关于加法和乘法构成一个环。
环如果还满足以下条件，则被称为交换环：

乘法的交换律：对于R中任意元素a、b，有ab=ba成立。

偶整数集合记为S，在普通加法和乘法运算下是交换环。而矩阵运算不满足交换律，所以上面的n阶方阵集合就不是交换环。整数{0，1，…，n-1}的集合Z 加上模n的算术运算构成一个交换环。

满足以下公理的交换环，称为整环：

乘法单位元：在R中存在元素1，使得对于R中的任意元素a，有a1=1a=a成立。
无零因子：如果有R中元素a、b，且ab=0，则必有a=0或b=0。

将普通加法和乘法运算下的整数集合记为S，则S是一个整环。

域

域F，记为{F，+，x}，是有两个二元运算的集合，对于F中的任意元素a、b、c满足以下公理：

F是一个整环，因此F满足整环的所有原则。
乘法逆元：对于F中的任意元素a(除0以外)，F中都存在一个元素a^-1使得下式成立：aa^-1 = (a^-1)a = 1

有限域GF( p )(伽罗华域Galois Fields)

有限域的阶(元素的个数)必须是一个素数的幂pⁿ，n为正整数。(后面讨论为什么p必须是素数)
阶为pⁿ的有限域一般记为GF(pⁿ)，主要研究两种特殊情形：n=1时的有限域GF( p )，它和n>1的有限域相比有着不同的结构；另一种是GF(2ⁿ)形式的有限域。

阶为p的有限域

给定一个素数p，元素个数为p的有限域GF（p）被定义为整数{0，1，…，p-1}的集合Z，其运算为模p的算术运算。
在GF（p）中加法和乘法就是普通加法和乘法后再对结果取模p。
减法是根据加法来定义的，a-b=a+(-b)。（-b是b的逆元）
除法根据乘法来定义，a/b=a x (b^-1)。这里需要用到域的乘法逆元的原则，容易知道GF（p）的单位元e=1，那么乘法逆元就是对GF（p）的一个数a，
a x a^-1=1（mod p）。
因此对于GF（p）中a除以b就是a / b=a x (b^-1)=c，满足b x c=a（mod p）的这个数c就是a除以b的结果。
p为什么一定是素数。
因为根据之前的讨论，对于乘法逆元的存在性，模运算与普通运算是不同的，必须有一个附加条件，GF（p）定义的集合Z中的任一整数a有乘法逆元当且仅当a与p互素。所以当p为素数，GF（p）中的所有非零整数都有乘法逆元。从上面的模8运算可以看出，它并不是一个有限域，不是所有非零元素都有乘法逆元。

在GF（p）中求乘法逆元

对于数值较大的p，无法直接看出乘法逆元，可以通过扩展的欧几里得算法求出乘法逆元。
对于正整数b [(ax mod a) + (by mod a)] mod a=1 mod a
0 + (by mod a) = 1，通过扩展的欧几里得算法，求出y=b^-1就是b的乘法逆元。

多项式运算

可以把多项式运算分为3种：
使用代数基本规则的普通多项式运算。
系数运算是模p运算的多项式运算，即系数在GF（p）中。
系数在GF（p）中，且多项式被定义为模一个n次多项式m(x)的多项式运算。
其中第三种在之后讨论。

普通多项式运算

n次多项式的表达形式：

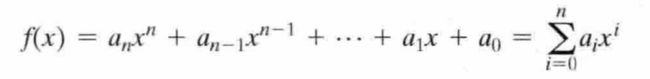
其中a_i是某个指定数集S中的元素，该数集叫做系数集，且a_n≠0。称f(x)是定义在系数集S上的多项式。
零次多项式称为常数多项式，仅仅是系数集中的一个元素。
如果a_n=1，那么对应的n次多项式称为首1多项式。
变元x称为不定元。
多项式运算包括加法，减法和乘法，当系数集S是域时，可以定义除法。注意整数集不是域，不支持多项式除法运算。

系数在Z_p中的多项式运算

系数是域F的元素的多项式称为域F的多项式，
对于域上的多项式，除法可以定义为：给定n次多项式f(x)和m次多项式
g(x)，(m≤n)，如果用g(x)除f(x)，我们得到一个商q(x)和一个余数r(x)，满足如下关系式：f(x)=q(x)g(x)+r(x)
其中f(x)是n次，g(x)m次，q(x)n-m次，r(x)≤m-1。如果r(x)=0，可以说g(x)整除f(x)，写为g(x)|f(x)；也可以说g(x)是f(x)的一个因式。
其中GF(2)上的多项式很有意义，在GF(2)上的多项式运算，加法等价于XOR运算，乘法等价于逻辑与运算，并且模2的加法与减法是等价的。

域F上的多项式称为不可约的，当且仅当f(x)不能表示为两个多项式的积。不可约多项式也被称为素多项式。

求最大公因式

如果c(x)能同时整除a(x)和b(x)，a(x)和b(x)的任何因式都是c(x)的因式，则称c(x)为a(x)和b(x)的最大公因式
通过改写欧几里得算法可以计算两个多项式的最大公因式
gcd[a(x)，b(x)]=gcd[b(x)，a(x) mod b(x)]。

有限域GF(2ⁿ)

动机

上面讨论了n=1时的有限域GF（p）上的运算，但这里p必须取素数，假设我们构造一个图像加密算法，需要在像素0~255这个范围上运算，但256并不是一个素数，小于256的最大素数是251，所以要使用以251为模的运算，但这样251-255就没法表示出了，可以将251-255分成两部分来表示，但会麻烦一些。
所以为了方便使用和提供效率，我们希望这个整数集中的数与给定的二进制位数所能表达的信息一一对应而不出现浪费。也就是希望整数集的范围是从0到2ⁿ-1，正好对应一个n位的字。但直接以2ⁿ（n＞1）为模是不行的，这样的整数集并不是一个域，即使我们只需要加密算法使用加法和乘法，以2ⁿ为模也存在问题。
我们需要借助多项式算术构造一个包含2ⁿ个元素的集合，其上定义了加法和乘法使之成为一个域。给集合的每一个元素赋值为0到2ⁿ-1之间的唯一整数。

多项式模运算

构造的多项式集合S包括以下定义：

①该运算遵循代数基本规则中的普通多项式运算规则及如下两条限制。
②系数运算以p为模，即遵循有限域Z_p上的运算规则。
③如果乘法运算的结果是次数大于n-1的多项式，那么必须将其除以某个次数为n的不可约多项式m(x)并取余式。对于多项式f(x)，这个余数可表示为r(x)=f(x)
mod m(x)。

所以有限域GF(2ⁿ)中加法就是按位做异或运算，乘法则需要选择一个不可约多项式，如果乘法运算的结果是次数大于n-1的多项式就除以这个不可约多项式取余式。

计算上的考虑

GF(2ⁿ)中的每个多项式
都可以表示成一个n位的二进制整数。

加法
多项式加法是将相应的系数分别相加，而对于Z₂上的多项式，加法就是异或运算。所以GF(2ⁿ)中的两个多项式加法等同于按位异或运算。

乘法
以AES中有限域为例，不可约多项式m(x)=x⁸+x⁴+x³+x+1，如果两个多项式相乘得到的结果是一个次数小于8的多项式，就不用继续运算，如果大于等于8，就进行模m(x)的约化。
这种乘法可以拆分成多次按位移和按位异或的运算来进行。

使用生成元

定义：

阶为q的有限域F的生成元是一个元素，记为 g , 该元素的前q-1个幂构成了F的所有非零元素，即域F的元素为0，g⁰，…，g^q-2。考虑由多项式f(x)定义的域F,如果F内的一个元素b满足f(b)=0，则称b为多项式的f(x)的根。最后，可以证明一个不可约多项式的根g是这个不可约多项式定义的有限域的生成元.

---