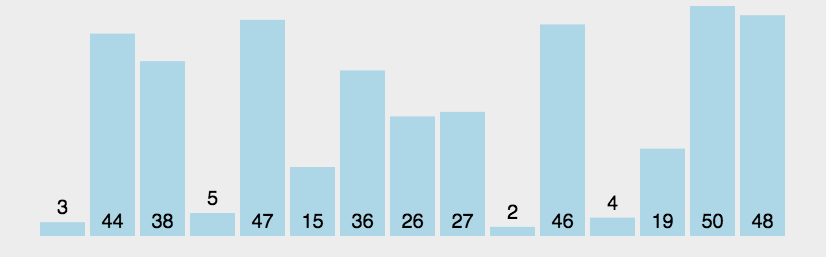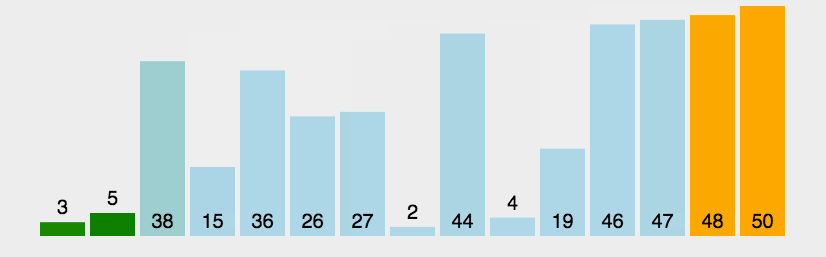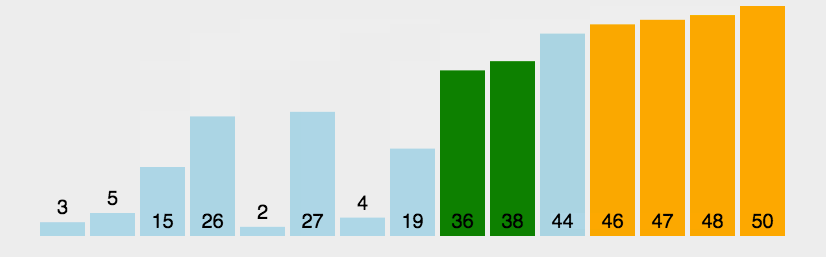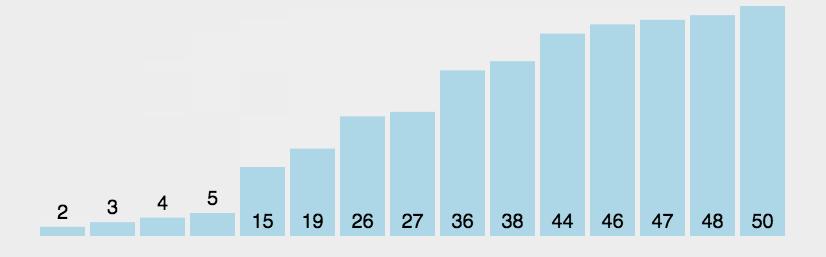在chapter0 中,我们设计了一个产品,叫私人衣橱。这个手机app帮助我们管理衣物,方便我们查找衣物的位置,也可以展示我们的衣服。
现在这个app要添加新功能:
- 找出过去一年中,自己最不常用的10件物品,看是否需要转卖或者扔掉。
怎么实现这个功能呢?方法有很多,我们先来介绍第一种方法:
“堆”
这个堆不是土堆、人堆,而是数据的堆。
特征
计算机语言里的描述:堆是指一个特定的基于树结构的数据结构。
我们先不管这个抽象的描述,我们只需要记住堆的特征:
一.任何一个节点不大于父亲节点(大根堆)
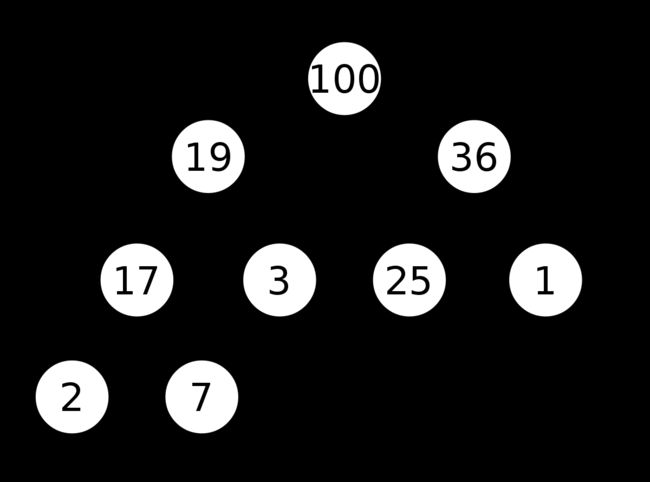
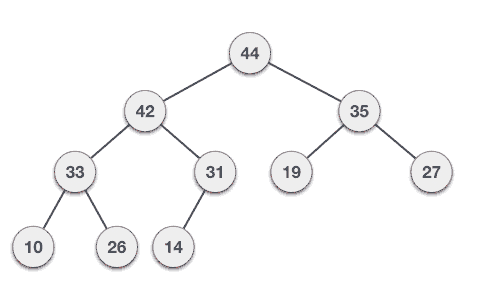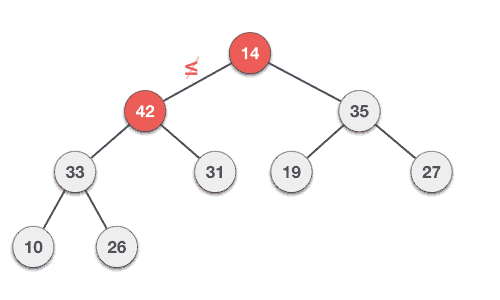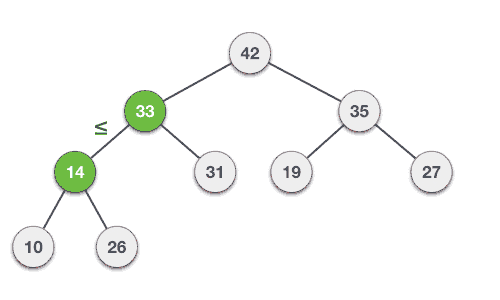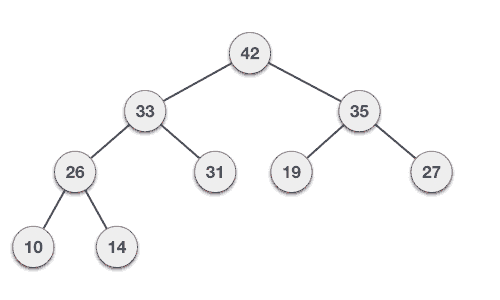
比如下面这幅图,2的父节点是17,17的父节点是19,是不是子节点小于父节点。不过19不是2的父节点,因为中间跨了一层。其他以此类推。100叫根节点,因为它已经到顶了,没有父节点。
二.它必须是一棵完全二叉树:就是除了最后一层节点外,其他层节点数必须是两个,最后一层的所有节点集中在最左侧。
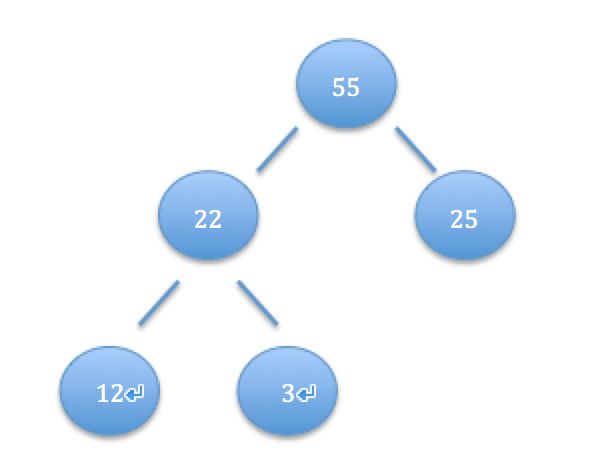
如下图:
它是一个正确的例子:55必须有两个子节点:22;25。22和25 不一定是有两个子节点,因为他们已经最后一层。
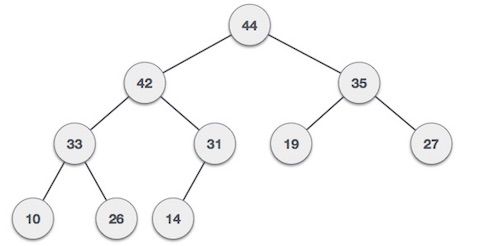
又如下图:
它是一个错误的例子,为什么?最后一层的所有节点没有集中在最左侧。因为子节点必须从上往下,从左往右添加。
了解完堆的概念,那么堆有哪些分类呢?
首先是:大根堆,即根节点的值最大,逐层递减,最下面一层的数据最小。
再次是小根堆:正好和大根堆相反。
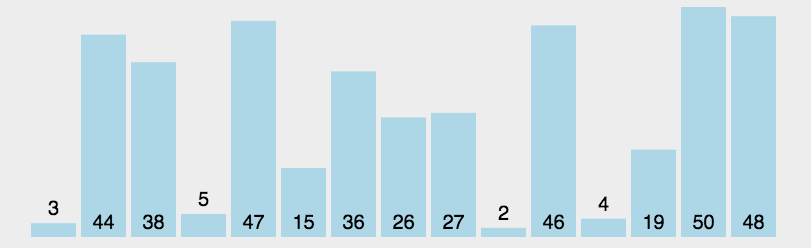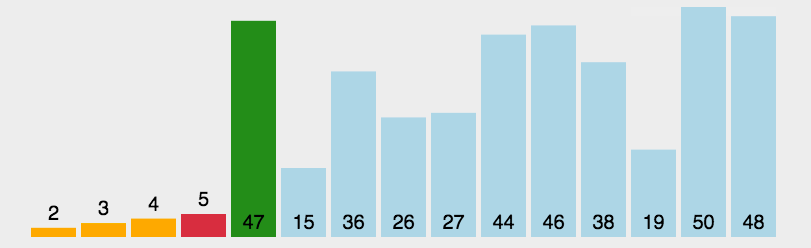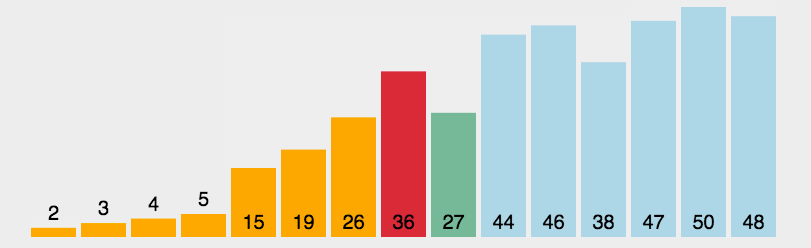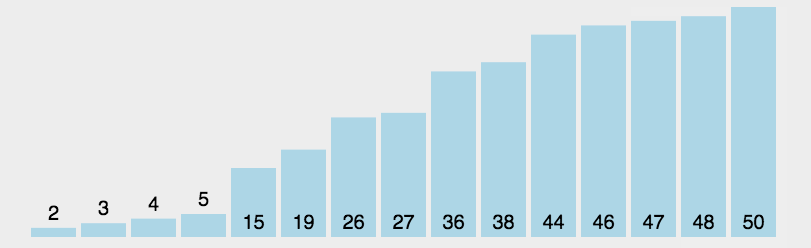
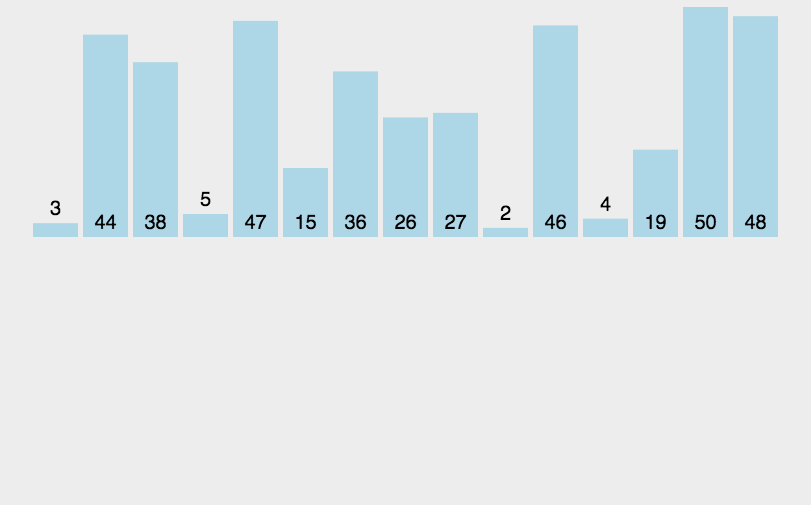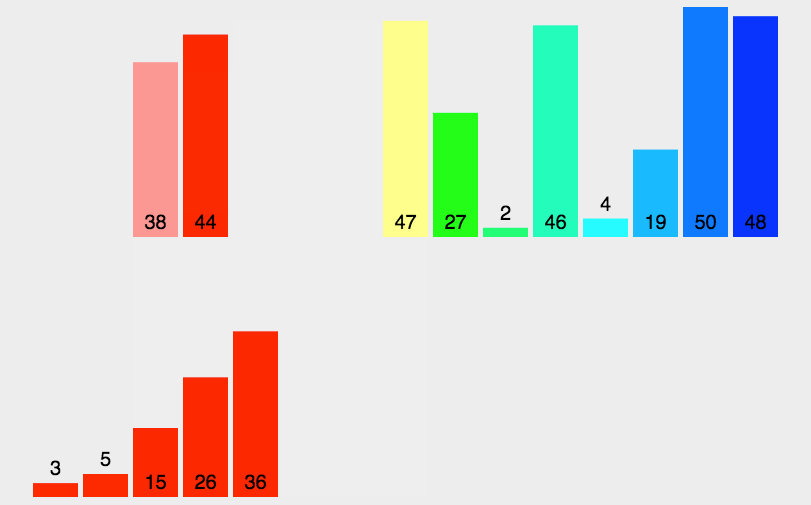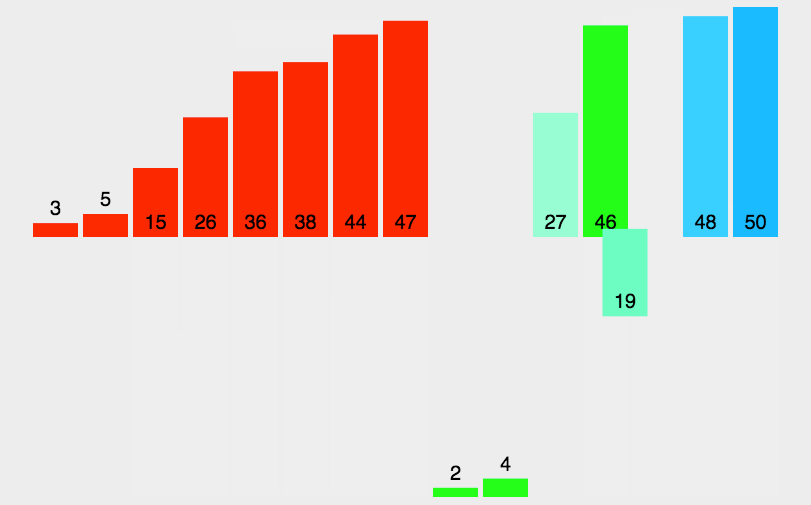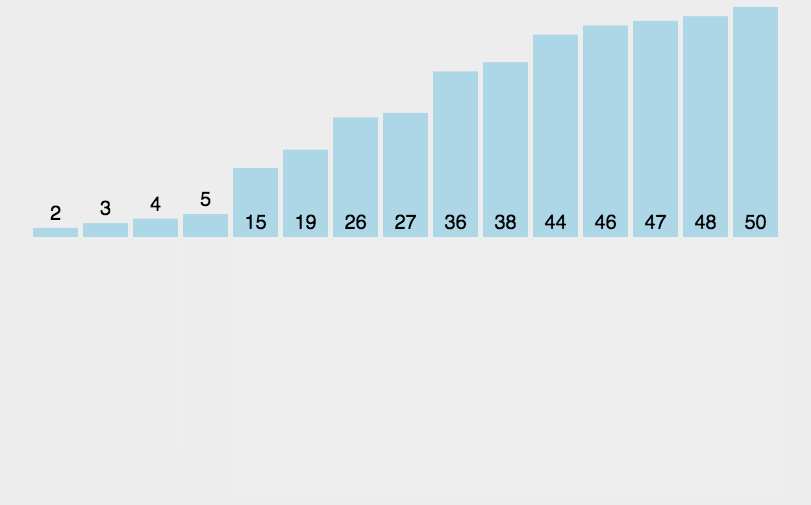
介绍完堆,我们回到上面的问题,假设我们有一系列的衣物,他们的使用频率分别是:35 33 42 10 14 19 27 44 26 31,我们将组数据构建成一个大根堆,从下往上层级的节点必然是小的值。
最终的结果是这样的:
具体构建大根堆的步骤:
Step 1 − 在堆的底部创建一个新节点
Step 2 − 将值放在该节点
Step 3 − 比较新关键的节点值与它的父节点值大小
Step 4 − 如何父节点值小于新节点值,那么交换他们
Step 5 − 重复第三步和第四部
好了,现在堆创建好,我们需要将频率最低的几个数据取出,堆是一种特殊的树(一种数据结构,后面再介绍),遍历数据有两种方式:广度遍历和深度遍历,方式如名字:
广度遍历方向:
遍历出来的数据是:
44 42 35 33 31 19 27 10 26 14
深度遍历方向:
遍历出来的数据是:
44 42 33 10 26 31 14 35 19 27
利用广度遍历,已经基本是从大到小了,后面的几个就已经基本满足我们的要求了。而且我们还可以知道,根节点就是我们使用频率最高的衣物。
但是我们也发现,广度遍历出来的数据,并不绝对是最后一个数据就是频率最低,这个怎么解决呢?
解决办法是:
排序
将使用频率:35 33 42 10 14 19 27 44 26 31,这组数据进行从高到底排序。也就实现我们的功能。
那排序的算法怎么设计呢?
选择排序(常规思维想到的第一个方法)
思想:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
算法描述
n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下:
- 初始状态:无序区为R[1..n],有序区为空;
- 第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1..i-1]和R(i..n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
- n-1趟结束,数组有序化了。
冒泡排序
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
算法描述
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
- 针对所有的元素重复以上的步骤,除了最后一个;
- 重复步骤1~3,直到排序完成。
归并排序(Merge Sort)
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
算法描述
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
-
将两个排序好的子序列合并成一个最终的排序序列。
基数排序(Radix Sort)
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。
算法描述
- 取得数组中的最大数,并取得位数;
- arr为原始数组,从最低位开始取每个位组成radix数组;
-
对radix进行计数排序(利用计数排序适用于小范围数的特点);
排序的算法还有很多,就不一一介绍了。
总结
选择排序:不停找最小值(效率也是最低的)
冒泡排序:相邻比较,不停交换,冒泡
归并排序:分组,不同组之间比较
基数排序:非比较类算法,先低优先级再高优先级排序
上面的堆也是也可以达到排序的目的。
通过排序,我们就可以得到降序的一个数组:
10 14 19 26 27 31 33 35 42 44
还怕找不到你最不常用的衣物吗?好了,最不常用的衣物已经找到了,快去处理掉把。
其他知识
堆的删除
从叶子开始添加,删除的时候从根节点开始删除。
具体的步骤是:
Step 1 − 删除根节点.
Step 2 − 移动最近一层的最近一个元素到根节点位置
Step 3 − 比较它与子节点值的大小
Step 4 − 加入父节点值小于子节点值,则相互交换
Step 5 − 重复第三步和第四步
排序图来自https://www.cnblogs.com/onepixel/articles/7674659.html