栈与队列(Java实现)
目录
一、栈Stack
1.定义:
2.三个常用方法:
3.实现基于数组的顺序栈
二、队列Queue
1.定义
2.常用操作:
3.分类
4.基于链表的基础队列的实现
三、栈与队列的互转
1.用栈实现队列(两个栈):
2.用队列实现栈(两个队列):
3.用队列实现栈(一个队列)
四、双端队列(Deque)
五、循环队列
1.定义
2.判空与判满
3.获取最后一个元素的索引:
4.代码实现
一、栈Stack
1.定义:
栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则
实际应用:常见的诸如撤销操作,网页后退操作,以及开发中程序的“调用栈”操作系统栈底层
2.三个常用方法:
push方法——入栈
pop方法——出栈,即将栈顶元素删除并返该元素
peek方法——返回栈顶元素
3.实现基于数组的顺序栈
为什么选用数组呢,其实链表也可以,但是我们想想,由于栈只能在栈顶进行增删,转化为数组,就是对数组的尾部进行增删,那么是很好实现的,时间复杂度仅为O(1),比链表要优越,所有这里我们选用数组实现栈
代码实现:
import java.util.ArrayList;
import java.util.List;
import java.util.NoSuchElementException;
//自己用数组实现泛型顺序栈
public class myStack {
// size存储栈中元素个数
private int size;
// 用动态数组实现存储元素
private List data = new ArrayList();
// 入栈-push方法
public void push(E value) {
// add方法默认为尾插
data.add(value);
// 记得更新size
size++;
}
// 出栈-pop方法,并返回出栈的元素
public E pop() {
if (isEmpty()) throw new NoSuchElementException("stack is empty!can not pop!!!");
else {
return data.remove(--size);
}
}
// 返回栈顶元素-peek方法
public E peek() {
if (isEmpty()) {
throw new NoSuchElementException("stack is empty!can not peek!!!");
} else {
return data.get(size - 1);
}
}
// 辅助方法,判空
public boolean isEmpty() {
return size == 0;
}
// toString方法
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append("[");
for (int i = 0; i < size - 1; i++) {
sb.append(data.get(i));
sb.append(", ");
}
sb.append(data.get(size - 1) + "]top");
return sb.toString();
}
} 我们可以对我们实习的栈进行测试,测试代码如下:
public class Test {
public static void main(String[] args) {
myStack my = new myStack<>();
// 入栈
my.push(3);
my.push(4);
my.push(5);
System.out.println(my);
// 出栈
System.out.println(my.pop());
System.out.println(my);
// 返回栈顶
System.out.println(my.peek());
}
} 执行结果:
[3, 4, 5]top
5
[3, 4]top
4
二、队列Queue
1.定义
- 队列也是一种特殊的线性表,只允许在一端进行插入数据操作,在 另一端 进行删除数据操作
- 和栈不同,队列中的元素遵守先进先出规则,FIFO(FirstIn First Out)
- 入队——进行插入操作的一端称为队尾
- 出队——进行删除操作的一端称为队头
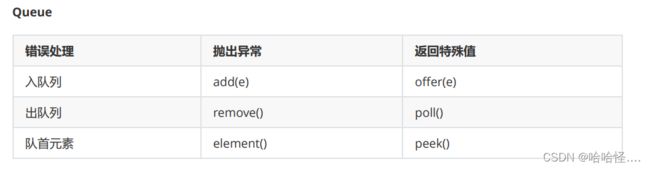
2.常用操作:
offer方法——入队
poll方法——出队
peek方法——返回队首元素
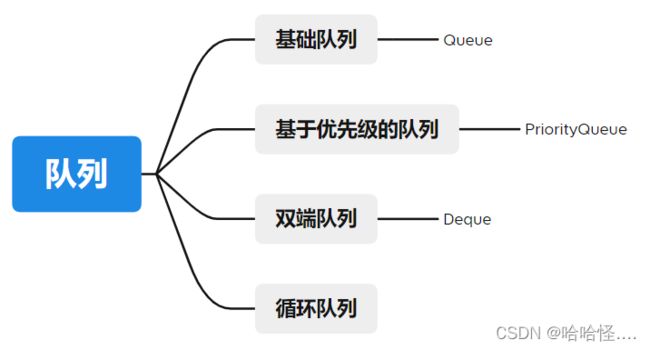
3.分类
队列的子类比栈要复杂一些:
- 基础队列(FIFO)
- 基于优先级的队列
- 循环队列
- 双端队列
但所有的这些子类都要有最基础的上述三个方法,所以我们可以定义一个队列接口,再让子类去实现接口
4.基于链表的基础队列的实现
这里,因为每次出队都是从队首出,再使用数组时间复杂度为O(n),所以使用链表的结构实现更优
代码实现:
接口:
//队列接口
public interface IQueue {
// 入队
void offer(E value);
// 出队
E poll();
// 返回队首元素
E peek();
// 判空
boolean isEmpty();
} 实现类:
import queue.IQueue;
import java.util.NoSuchElementException;
//基于链表的基础队列实现
public class MyQueue implements IQueue{
// 内部类,链表的每个节点
private class Node {
E value;
Node next;
public Node(E value) {
this.value = value;
}
}
// 长度,队首,队尾
private int size;
// head指向队首
private Node head;
// tail指向队尾
private Node tail;
// 入队
@Override
public void offer(E value) {
Node node = new Node(value);
// 如果是空的
if(isEmpty()){
head = tail = node;
}
// 否则,从队尾插入
else{
tail.next = node;
tail = node;
}
size ++;
}
@Override
public E poll() {
if(isEmpty()){
throw new NoSuchElementException("the queue is empty and can not poll");
}
else{
E value = head.value;
Node node = head;
head = head.next;
node.next = null;
size --;
return value;
}
}
@Override
public E peek() {
if(isEmpty()){
throw new NoSuchElementException("the queue is empty and can not peek");
}
else{
return head.value;
}
}
@Override
public boolean isEmpty() {
return size == 0;
}
public String toString(){
StringBuilder s = new StringBuilder();
s.append("head[");
Node node = head;
while(node.next != null){
s.append(node.value + ",");
node = node.next;
}
s.append(node.value);
s.append("]tail");
return s.toString();
}
} 测试类:
public class Test {
public static void main(String[] args) {
MyQueue q = new MyQueue();
// 入队
q.offer(3);
q.offer(4);
q.offer(5);
System.out.println(q);
// 取队首
System.out.println(q.peek());
// 删除队首并返回
System.out.println(q.poll());
// 删除后的队列
System.out.println(q);
}
}执行结果:
head[3,4,5]tail
3
3
head[4,5]tail
三、栈与队列的互转
1.用栈实现队列(两个栈):
232. 用栈实现队列 - 力扣(LeetCode) (leetcode-cn.com)
题目:请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
思路:
- 相同的插入顺序,栈与队列的删除顺序正好相反
- 使用两个栈s1,s2, 其中s1是目标栈,要使s1中元素出栈顺序与队列出队顺序一样,s2是辅助栈,借助s2使s1出栈顺序与队列顺序一样;
- 添加元素n时,如果s1是空的,直接入s1
- 否则将s1中的全部元素按出栈顺序插入s2中,直到s1为空,这时,再将n添加进s1,并将s2中的元素依次再添加进s1。
- 上述过程,借助s2,将s1中元素顺序正好颠倒,使颠倒后的出栈顺序与队列顺序一样
代码:
class MyQueue {
Stack s1;
Stack s2;
// 构造
public MyQueue() {
s1 = new Stack<>();
s2 = new Stack<>();
}
// 入队
public void push(int x) {
// 如果s1为空,直接入栈
if (s1.isEmpty()) {
s1.push(x);
} else {
// 否则将s1中元素全部放入s2中
while (!s1.isEmpty()) {
s2.push(s1.pop());
}
s1.push(x);
// x入s1后,再将s2中的全部入s1
while (!s2.isEmpty()) {
s1.push(s2.pop());
}
}
}
// 出队
public int pop() {
return s1.pop();
}
// 返回队首
public int peek() {
return s1.peek();
}
// 判空
public boolean empty() {
return s1.isEmpty();
}
} 2.用队列实现栈(两个队列):
225. 用队列实现栈 - 力扣(LeetCode) (leetcode-cn.com)
题目描述:
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
思路:
- 与1用栈实现队列思路类似,但注意,这里可以巧妙利用交换引用,达到颠倒顺序
- 还是两个队列q1和q2,假如刚开始元素n1入q1,再入n2时,交换q1,q2引用名称,将n1入q2,再将n2入q2,这时的q2实则就是正确的顺序,所以我们可以交换一次q1,q2指向,再入n3时,将n3入q1,再将q1中的n2,nq加入q2,再交换q1,q2顺序,始终保持q2为正确顺序
代码:
class MyStack {
Queue q1;
Queue q2;
// 构造
public MyStack() {
q1 = new LinkedList<>();
q2 = new LinkedList<>();
}
// 入栈,交换引用后q2为正确顺序
public void push(int x) {
if(q1.isEmpty()) {
q1.offer(x);
}
while (!q2.isEmpty()) {
q1.offer(q2.poll());
}
Queue q3 = q1;
q1 = q2;
q2 = q3;
}
// 出栈
public int pop() {
return q2.poll();
}
// 返回栈顶
public int top() {
return q2.peek();
}
// 判空
public boolean empty() {
return q2.isEmpty();
}
} 3.用队列实现栈(一个队列)
还是上题,其实我们可以发现,仅使用一个队列也可以实现栈
每次入队后,将队列中的元素从队首出队再重新入队,顺序也颠倒过来了
代码:
class MyStack {
Queue q1;
Queue q2;
public MyStack() {
q1 = new LinkedList<>();
}
public void push(int x) {
q1.offer(x);
int n = q1.size();
for (int i = 0; i < n - 1; i++) {
q1.offer(q1.poll());
}
}
//其他方法直接返回即可,这里不再赘写
public int pop() {
return q1.poll();
}
public int top() {
return q1.peek();
}
public boolean empty() {
return q1.isEmpty();
}
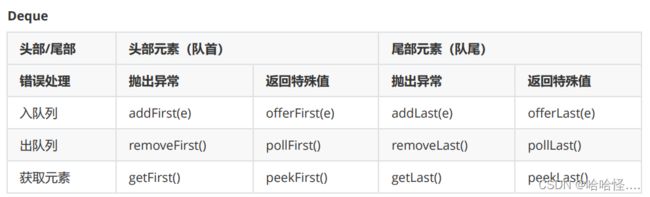
} 四、双端队列(Deque)
(1)指允许两端都可以进行入队和出队操作的队列;
说明元素可以从队头出队和入队,也可以从队尾出队和入队
(2)【注意】基于这一特性,双端队列尾插尾删或者头插头删其实就是实现了栈,所以:
我们使用双端队列Deque来代替JDK中Stack的使用,因为JDK中的Stack是线程安全的,效率极低
(3)Deque有两个子类:
ArrayDeque ——基于数组的双端队列
LinkedList ——基于链表的双端队列
JDK中内置的方法实现:
五、循环队列
1.定义
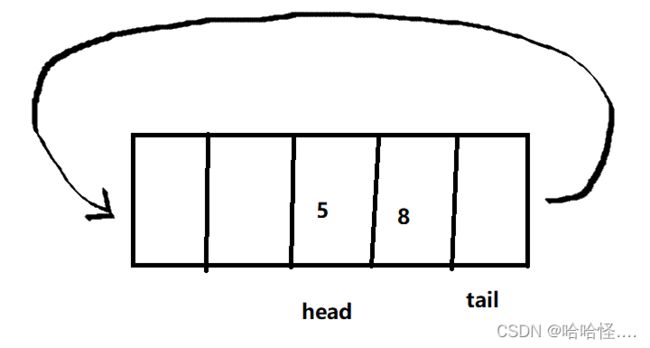
逻辑上成环,物理上还是线性表,通常使用数组来实现
head:队首元素索引
tail:队尾元素的下一个索引
增加/删除元素直接让head/tail向后移动,当走到数组末尾时,再从头开始走,直到数组已满
head = (head + 1) % length
tail = (tail + 1) % length
2.判空与判满
判空: heaad == tail
判满:(tail + 1) % length == head
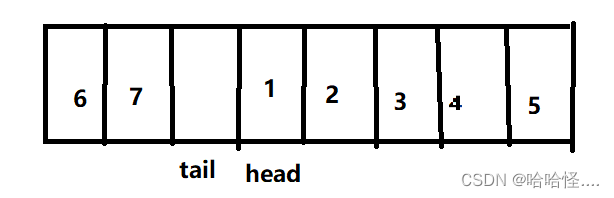
【注意】判满时,tail的下一个为head,是为了与判空区别开来,所以其实,循环队列会浪费一个空间
满:
3.获取最后一个元素的索引:
lastIndex = tail == 0 ? length - 1 : tail - 1
4.循环队列的优点:
1》 节省空间,避免数组空间浪费
2》删除元素只需head = head + 1,是逻辑上删除,解决了数组队列出队时需要搬移元素的问题
4.代码实现
622. 设计循环队列 - 力扣(LeetCode) (leetcode-cn.com)
//基于数组的循环队列
public class MyCircularQueue {
int[] a;
int head = 0;
int tail = 0;
// 构造方法
// 因为会浪费一个空间,所以切记要k + 1个单位
public MyCircularQueue(int k) {
a = new int[k + 1];
}
// 向循环队列插入一个元素。如果成功插入则返回真。
public boolean enQueue(int value) {
if (isFull()) {
return false;
}
a[tail] = value;
tail = (tail + 1) % a.length;
return true;
}
// 从循环队列中删除一个元素。如果成功删除则返回真
public boolean deQueue() {
if (isEmpty()) {
return false;
}
head = (head + 1) % a.length;
return true;
}
// 从队首获取元素。如果队列为空,返回 -1
public int Front() {
if (isEmpty()) {
return -1;
}
return a[head];
}
// 获取队尾元素。如果队列为空,返回 -1
public int Rear() {
if (isEmpty()) {
return -1;
}
return tail == 0 ? a[a.length - 1] : a[tail - 1];
}
// 判空
public boolean isEmpty() {
return head == tail;
}
// 判满
public boolean isFull() {
return (tail + 1) % a.length == head;
}
}