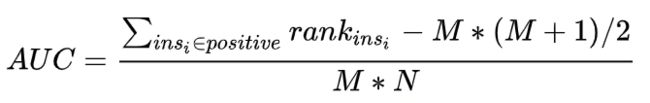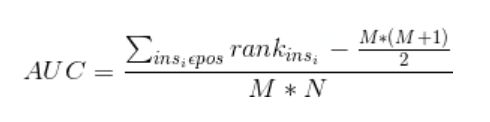机器学习篇-指标:AUC

AUC是什么东西？

AUC是一个模型评价指标，只能够用于二分类模型的评价，对于二分类模型来说还有很多其他的评价指标：
比如：logloss，accuracy，precision
在上述的评价指标当中，数据挖掘类比赛中，AUC和logloss是比较常见的模型评价指标
那么问题来了||ヽ(￣▽￣)ノミ|Ю为啥是AUC和logloss?
因为很多机器学习的模型对分类问题的预测结果都是概率，如果要计算accuracy的话，需要先将概率转换成类别，这就需要手动设置一个阈值，如果对一个样本的预测概率高于这个预测，就把这个样本放进一个类别当中，如果低于这个阈值，就放在另一个类别当中，阈值在很大程度上影响了accuracy的计算

使用AUC或者logloss的好处就是可以避免将预测概率转换成类别

AUC： Area under curve

字面理解：某条曲线下面区域的面积
问题来了，到底是哪一条曲线？
曲线的名字叫做：ROC曲线
ROC曲线讲解
(该内容来自于维基百科）

ROC分析的是二元分类模型，也就是输出结果只有两种类别的模型（垃圾邮件/非垃圾邮件）

当观测量的结果是一个连续值的时候，类与类的边界必须用一个阈值threshold来界定

举例来说，用血压值来检测一个人是否有高血压，测出的血压值是连续的实数（从0~200都有可能），以收缩压140／舒张压90为阈值，阈值以上便诊断为有高血压，阈值未满者诊断为无高血压。二元分类模型的个案预测有四种结局：P：positive N：negative

• 真阳性（TP）：诊断为有，实际上也有高血压。
• 伪阳性（FP）：诊断为有，实际却没有高血压。
• 真阴性（TN）：诊断为没有，实际上也没有高血压。
• 伪阴性（FN）：诊断为没有，实际却有高血压。

这四种结局可以画成2 × 2的混淆矩阵：

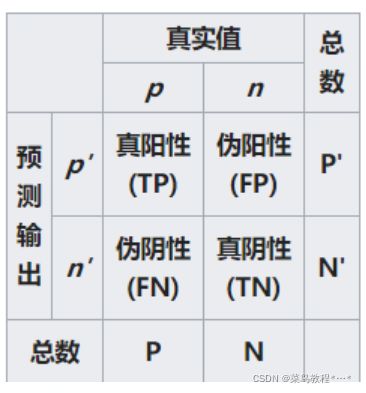
ROC空间将伪阳性率FPR定义为X轴，将真阳性率TPR定义为Y轴

TPR：在所有实际为阳性的样本中，被正确地判断为阳性之比率。

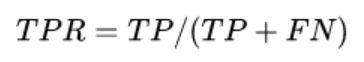
FPR：在所有实际为阴性的样本中，被错误地判断为阳性之比率。

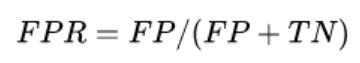
给定一个二元分类模型和它的阈值，就能从所有样本的（阳性／阴性）真实值和预测值计算出一个 (X=FPR, Y=TPR) 座标点。

从 (0, 0) 到 (1,1) 的对角线将ROC空间划分为左上／右下两个区域，在这条线的以上的点代表了一个好的分类结果（胜过随机分类），而在这条线以下的点代表了差的分类结果（劣于随机分类）。

完美的预测是一个在左上角的点，在ROC空间座标 (0,1)点，X=0 代表着没有伪阳性，Y=1 代表着没有伪阴性（所有的阳性都是真阳性）；也就是说，不管分类器输出结果是阳性或阴性，都是100%正确。一个随机的预测会得到位于从 (0, 0) 到 (1, 1) 对角线（也叫无识别率线）上的一个点；最直观的随机预测的例子就是抛硬币。

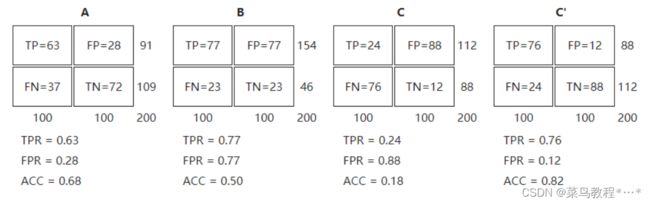
让我们来看在实际有100个阳性和100个阴性的案例时，四种预测方法（可能是四种分类器，或是同一分类器的四种阈值设定）的结果差异：

将这4种结果画在ROC空间里：

**离左上角越近的点预测（诊断）准确率越高。**离右下角越近的点，预测越不准。

在A、B、C三者当中，最好的结果是A方法。

B方法的结果位于随机猜测线（对角线）上，在例子中我们可以看到B的准确度是50%。

C虽然预测准确度最差，甚至劣于随机分类，也就是低于0.5（低于对角线）。然而，当将C以 (0.5, 0.5) 为中点作一个镜像后，C’的结果甚至要比A还要好。这个作镜像的方法，简单说，不管C（或任何ROC点低于对角线的情况）预测了什么，就做相反的结论。

上述ROC空间里的单点，是给定分类模型且给定阈值后得出的。但同一个二元分类模型的阈值可能设定为高或低，每种阈值的设定会得出不同的FPR和TPR。

将同一模型每个阈值 的 (FPR, TPR) 座标都画在ROC空间里，就成为特定模型的ROC曲线。

在同一个分类器之内，阈值的不同设定对ROC曲线的影响，仍有一些规律可循：

• 当阈值设定为最高时，亦即所有样本都被预测为阴性，没有样本被预测为阳性，此时在伪阳性率 FPR = FP / ( FP + TN ) 算式中的 FP = 0，所以 FPR = 0%。同时在真阳性率（TPR）算式中， TPR = TP / ( TP + FN ) 算式中的 TP = 0，所以 TPR = 0%
  –> 当阈值设定为最高时，必得出ROC座标系左下角的点 (0, 0)。

• 当阈值设定为最低时，亦即所有样本都被预测为阳性，没有样本被预测为阴性，此时在伪阳性率FPR = FP / ( FP + TN ) 算式中的 TN = 0，所以 FPR = 100%。同时在真阳性率 TPR = TP / ( TP + FN ) 算式中的 FN = 0，所以TPR=100%
  –>当阈值设定为最低时，必得出ROC座标系右上角的点 (1, 1)。
  因为TP、FP、TN、FN都是累积次数，TN和FN随着阈值调低而减少（或持平），TP和FP随着阈值调低而增加（或持平），所以FPR和TPR皆必随着阈值调低而增加（或持平）。
  –>随着阈值调低，ROC点 往右上（或右／或上）移动，或不动；但绝不会往左下(或左／或下)移动。

曲线下面积（AUC）

在比较不同的分类模型时，可以将每个模型的ROC曲线都画出来，比较曲线下面积做为模型优劣的指标。

意义

ROC曲线下方的面积（英语：Area under the Curve of ROC (AUC ROC)），其意义是：

因为是在1x1的方格里求面积，AUC必在0~1之间。

假设阈值以上是阳性，以下是阴性；

若随机抽取一个阳性样本和一个阴性样本，分类器正确判断阳性样本的值高于阴性样本之机率=AUC

简单说：AUC值越大的分类器，正确率越高。

从AUC判断分类器（预测模型）优劣的标准：

AUC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器。

0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。

AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。

AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

计算

AUC的计算有两种方式，都是以逼近法求近似值。

AUC为什么可以衡量分类的效果？

• AUC就是从所有1样本中随机选取一个样本，从所有0样本中随机选取一个样本，然后根据你的分类器对两个随机样本进行预测，把1样本预测为1的概率为p1，把0样本预测为1的概率为p2，p1>p2的概率就是AUC。所以AUC应该反映的是分类器对样本的排序能力，另外，AUC对样本类别是否均衡并不敏感，这也是不均衡样本通常采用AUC评价分类性能的原因

根据上面的推断，那么随机抽取一个样本，对应每一潜在可能值X都有对应一个判定正样本的概率P。

对一批已知正负的样本集合进行分类，按照预测概率从高到低进行排序，

对于正样本中概率最高的，排序为rank_1，

比它概率小的有M-1个正样本（M为正样本个数），（ranl_1-M）个负样本。

正样本中概率第二高的，排序为rank_2，

比它概率小的有M-2个正样本，（rank_2-(M-1)）个负样本，

以此类推，正样本中概率最小的，排序为rank_M，

比它概率小的有0个正样本，(rank_M-1)个负样本。

总共有M*N个正负样本对，把所有比较中正样本概率大于负样本概率的例子都算上，

得到公式：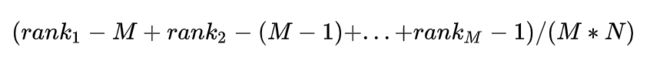
就是正样本概率大于负样本概率的可能性，将上述结果化简之后：

上述结果就是，AUC公式

AUC是现在分类模型中，特别是二分类模型使用的主要离线评测指标之一，相比于准确率，召回率，AUC有一个独特的优势，就是不管具体的得分，只关注于排序结果，这使得它特别适用于排序问题的效果评估

根据上面的公式求解AUC

首先对score从大到小排序，然后令最大score对应的sample的rank值为n，第二大score对应sample的rank值为n-1，以此类推从n到1。然后把所有的正类样本的rank相加，再减去正类样本的score为最小的那M个值的情况。得到的结果就是有多少对正类样本的score值大于负类样本的score值，最后再除以M×N即可。**值得注意的是，当存在score相等的时候，对于score相等的样本，需要赋予相同的rank值(无论这个相等的score是出现在同类样本还是不同类的样本之间，都需要这样处理)。**具体操作就是再把所有这些score相等的样本 的rank取平均。然后再使用上述公式。此公式描述如下：

def naive_auc(labels,preds):
    """
    最简单粗暴的方法
　　　先排序，然后统计有多少正负样本对满足：正样本预测值>负样本预测值, 
      再除以总的正负样本对个数。复杂度 O(NlogN), N为样本数
    """
    n_pos = sum(labels)
    n_neg = len(labels) - n_pos
    total_pair = n_pos * n_neg

    labels_preds = zip(labels,preds)
    labels_preds = sorted(labels_preds,key=lambda x:x[1])//从小到大，倒序计算
    accumulated_neg = 0
    satisfied_pair = 0
    for i in range(len(labels_preds)):
        if labels_preds[i][0] == 1:
            satisfied_pair += accumulated_neg
        else:
            accumulated_neg += 1

    return satisfied_pair / float(total_pair)

接下来还可以采用进一步加速的方法：

使用近似方式，将预测值分桶，对正负样本分别构建直方图，再统计满足条件的正负样本对

关于AUC还有一个很有趣的性质，它和Wilcoxon-Mann-Witney Test类似（可以去google搜一下），而Wilcoxon-Mann-Witney Test就是**测试任意给一个正类样本和一个负类样本，正类样本的score有多大的概率大于负类样本的score。**有了这个定义，就可以得到了另外一中计算AUC的方法：计算出这个概率值。我们知道，在有限样本中我们常用的得到概率的办法就是通过频率来估计之。这种估计随着样本规模的扩大而逐渐逼近真实值。样本数越多，计算的AUC越准确类似，也和计算积分的时候，小区间划分的越细，计算的越准确是同样的道理。具体来说就是： 统计一下所有的 M×N(M为正类样本的数目，N为负类样本的数目)个正负样本对中，有多少个组中的正样本的score大于负样本的score。当二元组中正负样本的 score相等的时候，按照0.5计算。然后除以MN。实现这个方法的复杂度为O(n^2 )。n为样本数(即n=M+N),公式表示如下：

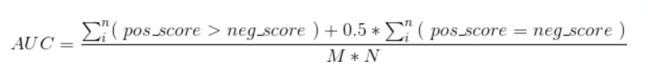
def approximate_auc(labels,preds,n_bins=100):
    """
    近似方法，将预测值分桶(n_bins)，对正负样本分别构建直方图，再统计满足条件的正负样本对
    复杂度 O(N)
    这种方法有什么缺点？怎么分桶？

    """
    n_pos = sum(labels)
    n_neg = len(labels) - n_pos
    total_pair = n_pos * n_neg

    pos_histogram = [0 for _ in range(n_bins)]
    neg_histogram = [0 for _ in range(n_bins)]
    bin_width = 1.0 / n_bins
    for i in range(len(labels)):
        nth_bin = int(preds[i]/bin_width)
        if labels[i]==1:
            pos_histogram[nth_bin] += 1
        else:
            neg_histogram[nth_bin] += 1

    accumulated_neg = 0
    satisfied_pair = 0
    for i in range(n_bins):
        satisfied_pair += (pos_histogram[i]*accumulated_neg + pos_histogram[i]*neg_histogram[i]*0.5)
        '''
        accumulated_neg统计当前bins之前有多少负样本桶，将其*pos_histogram[i] 等价于当前正样本桶有大于负样本桶
        pos_histogram[i]*neg_histogram[i]*0.5，有可能正样本桶和负样本桶落在同一个区间，当前区间无法计算，近似
        '''
        accumulated_neg += neg_histogram[i]

    return satisfied_pair / float(total_pair)

但是上述方法的问题在于：

预测值大多不是均匀分布在0-1之间的，分布特别不平衡的话，均匀分出来的桶就不太好，

采用频率进行划分桶，（均匀划分，等频划分）

进一步的尝试MapReduce如何计算AUC

MAP阶段：统计直方图

Reduce阶段：计算AUC的结果

上述完整代码：

#　coding=utf-8
#　auc值的大小可以理解为: 随机抽一个正样本和一个负样本，正样本预测值比负样本大的概率
# 根据这个定义，我们可以自己实现计算auc

import random
import time

def timeit(func):
    """
    装饰器，计算函数执行时间
    """
    def wrapper(*args, **kwargs):
        time_start = time.time()
        result = func(*args, **kwargs)
        time_end = time.time()
        exec_time = time_end - time_start
        print "{function} exec time: {time}s".format(function=func.__name__,time=exec_time)
        return result
    return wrapper

def gen_label_pred(n_sample):
    """
    随机生成n个样本的标签和预测值
    """
    labels = [random.randint(0,1) for _ in range(n_sample)]
    preds = [random.random() for _ in range(n_sample)]
    return labels,preds

@timeit
def naive_auc(labels,preds):
    """
    最简单粗暴的方法
　　　先排序，然后统计有多少正负样本对满足：正样本预测值>负样本预测值, 再除以总的正负样本对个数
     复杂度 O(NlogN), N为样本数
    """
    n_pos = sum(labels)
    n_neg = len(labels) - n_pos
    total_pair = n_pos * n_neg

    labels_preds = zip(labels,preds)
    labels_preds = sorted(labels_preds,key=lambda x:x[1])
    accumulated_neg = 0
    satisfied_pair = 0
    for i in range(len(labels_preds)):
        if labels_preds[i][0] == 1:
            satisfied_pair += accumulated_neg
        else:
            accumulated_neg += 1

    return satisfied_pair / float(total_pair)

@timeit
def approximate_auc(labels,preds,n_bins=100):
    """
    近似方法，将预测值分桶(n_bins)，对正负样本分别构建直方图，再统计满足条件的正负样本对
    复杂度 O(N)
    这种方法有什么缺点？怎么分桶？
    
    """
    n_pos = sum(labels)
    n_neg = len(labels) - n_pos
    total_pair = n_pos * n_neg
    
    pos_histogram = [0 for _ in range(n_bins)]
    neg_histogram = [0 for _ in range(n_bins)]
    bin_width = 1.0 / n_bins
    for i in range(len(labels)):
        nth_bin = int(preds[i]/bin_width)
        if labels[i]==1:
            pos_histogram[nth_bin] += 1
        else:
            neg_histogram[nth_bin] += 1
    
    accumulated_neg = 0
    satisfied_pair = 0
    for i in range(n_bins):
        satisfied_pair += (pos_histogram[i]*accumulated_neg + pos_histogram[i]*neg_histogram[i]*0.5)
        accumulated_neg += neg_histogram[i]
    
    return satisfied_pair / float(total_pair)

# 思考：mapreduce版本的auc该怎么写


if __name__ == "__main__":
    labels,preds = gen_label_pred(10000000)
    naive_auc_rst = naive_auc(labels,preds)
    approximate_auc_rst = approximate_auc(labels,preds)
    print "naive auc result:{},approximate auc result:{}".format(naive_auc_rst,approximate_auc_rst)

    """
    naive_auc exec time: 31.7306630611s
    approximate_auc exec time: 2.32403683662s
    naive auc result:0.500267265728,approximate auc result:0.50026516844
    """