LIS(最长上升子序列)（细化）

是个一维序列，然后一维序列就用一维表示就可以

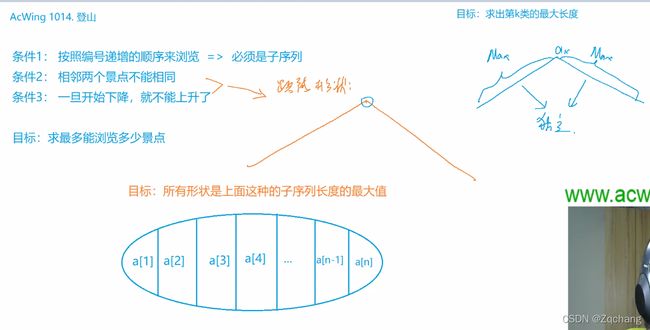
怪盗基德的滑翔翼

这个就是基德可以在任意一个点，向两个方向滑，然后就是正着做一遍lis，然后反着再做一遍，找出来这两种情况里面的，最长上升子序列

#include 
#include 
#include 

using namespace std;

const int N = 110;

int n;
int h[N];
int f[N];

int main()
{
    int T;
    scanf("%d", &T);
    while (T -- )
    {
        scanf("%d", &n);
        for (int i = 0; i < n; i ++ ) scanf("%d", &h[i]);

        int res = 0;
        for (int i = 0; i < n; i ++ )
        {
            f[i] = 1;
            for (int j = 0; j < i; j ++ )
                if (h[i] < h[j])
                    f[i] = max(f[i], f[j] + 1);
            res = max(res, f[i]);
        }

        memset(f, 0, sizeof f);
        for (int i = n - 1; i >= 0; i -- )
        {
            f[i] = 1;
            for (int j = n - 1; j > i; j -- )
                if (h[i] < h[j])
                    f[i] = max(f[i], f[j] + 1);
            res = max(res, f[i]);
        }

        printf("%d\n", res);
    }

    return 0;
}

登山
好像做过这题，，，

可以看作从左往右一遍最长上升子序列，然后从右往左一遍
最长下降不就是反着看的最长上升嘛，但是不能直接改大于号小于号，因为思路变了，在最长上升中，它的f[j]已经确定了，但是最长下降就没有，所以建议反过来上升
添加链接描述

#include 
#include 

using namespace std;

const int N = 1010;

int n;
int h[N];
int f[N], g[N];

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &h[i]);

    for (int i = 0; i < n; i ++ )
    {
        f[i] = 1;
        for (int j = 0; j < i; j ++ )
            if (h[i] > h[j])
                f[i] = max(f[i], f[j] + 1);
    }

    for (int i = n - 1; i >= 0; i -- )
    {
        g[i] = 1;
        for (int j = n - 1; j > i; j -- )
            if (h[i] > h[j])
                g[i] = max(g[i], g[j] + 1);
    }

    int res = 0;
    for (int i = 0; i < n; i ++ ) res = max(res, f[i] + g[i] - 1);

    printf("%d\n", res);

    return 0;
}

合唱队列

你看这个跟上一个是不是很像？
就是用n减去上一个的res

#include 
#include 

using namespace std;

const int N = 110;

int n;
int h[N];
int f[N], g[N];

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d", &h[i]);

    for (int i = 0; i < n; i ++ )
    {
        f[i] = 1;
        for (int j = 0; j < i; j ++ )
            if (h[i] > h[j])
                f[i] = max(f[i], f[j] + 1);
    }

    for (int i = n - 1; i >= 0; i -- )
    {
        g[i] = 1;
        for (int j = n - 1; j > i; j -- )
            if (h[i] > h[j])
                g[i] = max(g[i], g[j] + 1);
    }

    int res = 0;
    for (int i = 0; i < n; i ++ ) 
	{
		res = max(res, f[i] + g[i] - 1);
//		cout<<"i:"<
	}

    printf("%d\n", n-res);

    return 0;
}
/*
100
114 87 90 88 106 146 126 146 54 85 106 80 99 110 64 67 106 73 65 57 149 106 140 53 98 131 65 127 96 140 83 103 124 72 59 97 89 121 105 136 130 138 51 65 67 150 104 56 128 95 141 80 132 146 136 135 55 116 115 103 150 77 131 147 99 114 88 87 79 126 134 57 150 137 140 112 123 70 79 109 60 139 131 98 136 96 58 72 69 110 71 148 86 96 86 75 107 80 95 91
*/

友好城市

其实就是，按照一边排序，然后另一边对应就成了一个无序数组，然后把这个无序数组取一个最长上升子序列就行

就是图中，按照自变量大小，对因变量排序，然后取一个最长上升子序列，
图中一个合法的建桥方式就是上升子序列，上升子序列里面有几个，就代表有几个桥

思路：首先就是想一下什么情况下会有相交的情况出现，如果 我们按照下边的自变量的顺序，来看 我们依次建立的桥梁的话，只要每一个我们选出的点，它上面对应的点是单调的，序列没有出现交叉的情况 的话，就不会有桥梁交叉，反之，我们如果按照下面从小到大的顺序来看上边，如果出现了上面一些点的顺序是变得，那么它就一定会出现交叉的情况。因为只要出现一个逆序，就会出现交叉地情况。因此如果没有交叉，就必须在下边排完序之后，上边是一个单调的序列
怎么想到排序呢？其实是一种试的思路
给我们一个题目，我们怎么知道标准做法呢？就是先后想各种做法，靠经验

这个题更本质的是，如果选出来的桥，没有交叉的，我们按照其中某一个点来排序，那么另外一个点一定是有序的才行，因为一旦出现逆序，就会有交叉，没有交叉就意味着一定没有逆序

对于lis，除了贪心之外，还有一些数据结构可以优化成nlogn，比如（离散化）线段树，平衡树，

一般来说，在笔试面试中，这个（性质）思考过程很重要，就是先发现问题的某种性质，然后就简单了
平时练的时候多注意转换

一亿这个数比较离谱，他在超时的边缘，所以尽量不要到一亿

#include 
#include 

using namespace std;

typedef pair<int, int> PII;

const int N = 5010;

int n;
PII city[N];
int f[N];

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ ) scanf("%d%d", &city[i].first, &city[i].second);
    sort(city, city + n);

    int res = 0;
    for (int i = 0; i < n; i ++ )
    {
        f[i] = 1;
        for (int j = 0; j < i; j ++ )
            if (city[i].second > city[j].second)
                f[i] = max(f[i], f[j] + 1);
        res = max(res, f[i]);
    }

    printf("%d\n", res);

    return 0;
}

最大上升子序列和

这个要在dp问题的分析层面做一个分析，对分析的过程做一个变化。

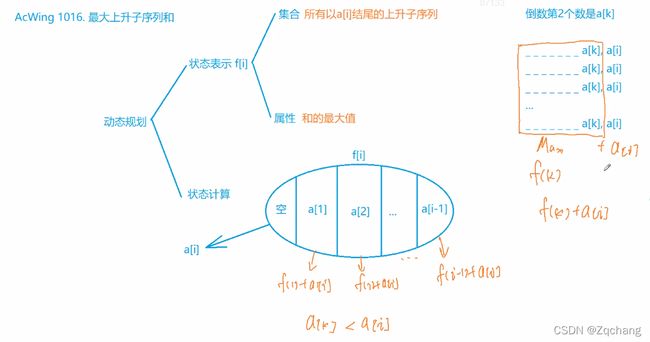
我们能够看出来，其实这个跟最长上升子序列还是挺像的，只不过把+1变成了+a[i]

#include 
#include 

using namespace std;

const int N = 1010;

int n;
int w[N];
int f[N];

int main()
{
    scanf("%d", &n);

    for (int i = 0; i < n; i ++ ) scanf("%d", &w[i]);

    int res = 0;
    for (int i = 0; i < n; i ++ )
    {
        f[i] = w[i];
        for (int j = 0; j < i; j ++ )
            if (w[i] > w[j])
                f[i] = max(f[i], f[j] + w[i]);
        res = max(res, f[i]);
    }

    printf("%d\n", res);

    return 0;
}

再看导弹拦截

第二问的分析过程：
要使用贪心法：
其中A表示贪心得到的序列个数，B表示最优解
B<=A很显然，最优解的序列一个小于等于贪心啊
使用调整法证明A<=B
首先就是，假设

a显然就是小于等于这个数的最小的那一个，然后b一定>=a,假设这个数就是x

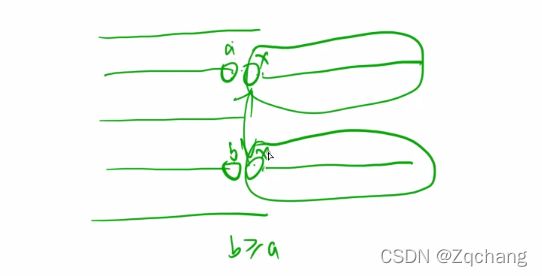
因此可以得到就是，a还有圈出来的两个部分相同且可以换到b，交换完之后，还是合法方案，并没有增加子序列的个数，因此贪心和最优不一样，我们找到第一个不同的地方，我们可以通过交换，把最优解变成贪心法，并且每一次调整，都没有增加子序列的个数，因此贪心法得到子序列的个数，小于等于最优解子序列个数的

实现方式，我们可以开一个数组来存每个序列的结尾，然后就发现，g数组是个单调上升的
然后就可以发现 ，这个g数组的维护，跟nlogn的lis的做法一样，就可以得出结论：一个序列，最少用多少个非上升的子序列把它覆盖掉的方案数，等于最长上升子序列的方案数的
这两个问题是一个对偶问题，在离散中称之为反链定理，也叫Dilworth定理
注意这个题的读入，可能要用到stringstream

#include 
#include 
#include 

using namespace std;

const int N = 1010;

int n;
int h[N], f[N], q[N];

int main()
{
    while (cin>>h[n]) n ++ ;

    int res = 0;
    for (int i = 0; i < n; i ++ )
    {
        f[i] = 1;
        for (int j = 0; j < i; j ++ )
            if (h[i] <= h[j])
                f[i] = max(f[i], f[j] + 1);
        res = max(res, f[i]);
	}
	
	cout << res << endl;
	
	int cnt =0;
	for(int i=0; i<n; i++)
	{
        int k = 0;//是我们从前往后找的序列 
        while (k < cnt && q[k] < h[i]) k ++ ;
        if (k == cnt) q[cnt ++ ] = h[i];
        else q[k] = h[i];
    }

    printf("%d\n", cnt);
    return 0;
}

导弹拦截系统
这个题没有什么很好的做法，他跟上一道题不同，上一道题贪心的时候只需要考虑两种情况，是属于哪一个子序列的后边，还是要新建一个子序列，但是这个题目在决定这两个情况之前，还要选择是用上升子序列还是下降子序列，所以，建议直接爆搜

爆搜的空间大概是$2^n$级别
这里可以将dfs求最小步数问题划分为两种情况：第一个是记一个全局变量的最小值，然后不停的更新它，第二种是迭代加深（这两个也就是dfs的求最小值方法）
这两种方法在题目视频讲解中都有，这里写一个记录全局最小值
bfs求最小值容易爆栈，bfs把没层都存下来，没层有指数级别的空间
dfs就是存一个路径，是线性的
而且bfs不好剪枝，dfs好减枝
这里向量太难定义了，这里的状态相当于有su个上升子序列，sd个下降子序列，相当于要存一个su+sd维的向量，也就是我们的状态是一个su+sd维的数组，太难存了，也就是本题所以dfs

建议把另一个做法也看了，我之后会补上

#include 
#include 

using namespace std;

const int N = 55;

int n;
int h[N];
int up[N], down[N];//up表示上升子序列的结尾，down表示下降子序列的结尾 
int ans;

void dfs(int u, int su, int sd)//u是当前枚举到了第几个数，su是当前上升子序列的个数，sd是当前下降子序列的个数 
{
    if (su + sd >= ans) return;//dfs很快找到一组解，ans就很小了，所以效果跟迭代加深差不多
    if (u == n)
    {
        ans = min(ans, su + sd);
        return;
    }
	//将当前数放到上升子序列里面 
    int k = 0;
    while (k < su && up[k] >= h[u]) k ++ ;
    if (k < su)
    {
        int t = up[k];//备份现场，方便回溯 
        up[k] = h[u];
        dfs(u + 1, su, sd);
        up[k] = t;
    }
    else
    {
        up[k] = h[u];
        dfs(u + 1, su + 1, sd);
    }
	//将当前数放到下降子序列里面 
    k = 0;
    while (k < sd && down[k] <= h[u]) k ++ ;
    if (k < sd)
    {
        int t = down[k];
        down[k] = h[u];
        dfs(u + 1, su, sd);
        down[k] = t;
    }
    else
    {
        down[k] = h[u];
        dfs(u + 1, su, sd + 1);
    }
}

int main()
{
    while (cin >> n, n)
    {
        for (int i = 0; i < n; i ++ ) cin >> h[i];

        ans = n;
        dfs(0, 0, 0);

        cout << ans << endl;
    }

    return 0;
}

最长公共上升子序列

最长公共上升子序列

这里的以b[i]结尾也可以写成以a[i]结尾，a和b是对称的，地位等同

我们先回忆一下我之前写的那个最长公共子序列，这跟我下面要说的没啥关系
好，压力来到我们这道题

很显然，状态是两维，f[i,j]，然后状态计算分为两部分，一部分是包含a[i],另一部分是不包含a[i]，很显然，不包含a[i]的就是f[i-1,j]，包含a][i]的话，就要注意到，a[i]和b[j]应该就是一样的，第二种情况不是很好直接求，没有任何一个状态可以直接表示它，也没法直接转化，那就直接分解，直到分解到能算为止，理论上来说，一定能划分到能算为止的，因为我们最不济的情况下就是每一种方案都是一个状态，每一种方案我们从实际意义去出发就能做了，所以只要算不了就能一直划分。这个过程是一直可以持续下去的，一定可以得到解的，因为最差就是爆搜。那我们这里怎么划分呢？由于a[i]已经固定了，所以我们可以回忆一下上升子序列怎么划分的。最后一个数确定之后，我们枚举的是最后一个变量，也就是枚举倒数第二个数的位置，我们根据倒数第二个数来划分，可以划分成j类，第一类还是只包含一个数，标记为空。也就是枚举一下b的前j-1个数，然后求每一类最大值，就从实际意义出发，就是看一下这个集合里面的上升子序列是啥，观察一下这个集合有什么特点，然后就是最后一个数都是b[j]就看除了b[j]之外，前边的，那些数的共同特点，就发现，假设倒数第二个是b[k]吧，然后就是a的前i-1（因为ai == bj，所以bj出去了，ai也得出去）个和b的前k个组成的最长子序列+1，就是f[i-1, k]。

这个题对代码做等价变形，还能优化掉一维
先来一个暴力写的，这个复杂度是$n^3$

#include 

using namespace std;

const int N = 3010;

int n;
int a[N], b[N];
int f[N][N];

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    for (int i = 1; i <= n; i ++ ) cin >> b[i];

    for (int i = 1; i <= n; i ++ )
    {
        
        for (int j = 1; j <= n; j ++ )
        {
            f[i][j] = f[i - 1][j];
            
            if (a[i] == b[j])//判断第二种情况存不存在 
            {
            	f[i][j] = max(f[i][j], 1);
            	for(int k=1; k<j; k++)
					if(b[k] < b[j])//判断每个小块存不存在 
						f[i][j] = max(f[i][j], f[i-1][k] + 1);//这里写成f[i][j]也行，因为上面已经写了f[i][j] = f[i-1][j] 
						
			}
        }
    }

    int res = 0;
    for (int i = 1; i <= n; i ++ ) res = max(res, f[n][i]);
    cout << res << endl;

    return 0;
}

开始变形

for (int j = 1; j <= n; j ++ )
        {
            f[i][j] = f[i - 1][j];
            
            if (a[i] == b[j])//判断第二种情况存不存在
            {
            	f[i][j] = max(f[i][j], 1);
            	for(int k=1; k<j; k++)
					if(b[k] < a[i])//判断每个小块存不存在  ,因为a[i]=b[j]所以把这里的b[j]换成 a[i]
					//这时候循环的含义就变了，就变成从1到j-1里面找到满足小于a[i]的f[i][k]的最大值，这时候发现，这个条件和j没有关系
//其实就是在满足一个和j没有关系的情况下，它某个前缀的最大值
//求前缀最大值的话，我们有一个常用的优化方式
//可以用一个变量，可以边循环边求，这样可以省去一个循环，就是，我们可以用一个变量来存储某一个前缀的最大值是多少
					//也就是可以把条件提到循环外面 
						f[i][j] = max(f[i][j], f[i-1][k] + 1);//这里写成f[i][j]也行，因为上面已经写了f[i][j] = f[i-1][j] 
						
			}
        }

优化之后呢

#include 

using namespace std;

const int N = 3010;

int n;
int a[N], b[N];
int f[N][N];

int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    for (int i = 1; i <= n; i ++ ) cin >> b[i];

    for (int i = 1; i <= n; i ++ )
    {
        int maxv = 1;//就是在满足b[k]
        for (int j = 1; j <= n; j ++ )
        {
            f[i][j] = f[i - 1][j];
            if (a[i] == b[j]) f[i][j] = max(f[i][j], maxv);

            if (b[j] < a[i])
                maxv = max(maxv, f[i - 1][j] + 1);
        }
    }

    int res = 0;
    for (int i = 1; i <= n; i ++ ) res = max(res, f[n][i]);
    cout << res << endl;

    return 0;
}

如果想不清楚，可以看看这个没省略版的，用一整个数组表示

#include 

using namespace std;

const int N = 3010;

int n;
int a[N], b[N];
int f[N][N];
int g[N][N]; //g[i][j]表示所有a[i] > b[j]的所有f[i-1][j]+1的最大值 ，这就是之前第三个循环要求的 
int main()
{
    cin >> n;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    for (int i = 1; i <= n; i ++ ) cin >> b[i];

    for (int i = 1; i <= n; i ++ )
    {
    	g[i][0] = 1; 
//        int maxv = 1;//就是在满足b[k]
        for (int j = 1; j <= n; j ++ )
        {
            f[i][j] = f[i - 1][j];
            if (a[i] == b[j]) f[i][j] = max(f[i][j], g[i][j-1]);
            //自认为，这里的更新是因为，下面已经加一了，所以就是去除了a[i]或者b[j]的最值然后又加上这俩，所以这里直接更新就行了
			g[i][j] = g[i][j-1];//因为这是前面所有的最大值，所以多一个的话，最小是它 
            if (b[j] < a[i])
                g[i][j] = max(g[i][j], f[i - 1][j] + 1);
        }
    }

    int res = 0;
    for (int i = 1; i <= n; i ++ ) res = max(res, f[n][i]);
    cout << res << endl;

    return 0;
}