本文的最新版本位于:https://github.com/iwhales/algorithms_notes
转载请注明出处:https://www.jianshu.com/u/5e6f798c903a
参考:《数据结构(Python 语言描述)》 - 3.3 搜索算法
学习思路按照以下三个层次推进:学习算法设计思路 >> 实现算法 >> 复杂度分析
Tips:为了保持简洁,每个函数都只处理一个整数列表,并且假设列表不为空。
1. 搜索最小值
Search for the Minimum
下面这个函数会返回列表中最小项的索引,该算法的复杂度是 O(n) 。
def index_of_min(lyst):
"""返回最小项的索引"""
min_index = 0
current_index = 1
while current_index < len(lyst):
if lyst[current_index] < lyst[min_index]:
min_index = current_index
current_index += 1
return min_index
2. 顺序搜索
顺序搜索(Sequential Search),也称线性搜索(linear search)。
如果需要在对象上使用 in 进行成员测试,则需要为该对象实现 __contains__() 方法。如果对象中包含指定项,返回 True;否则返回 False 。下面这个顺序搜索函数,实现了与列表中 __contains__() 方法类的功能。
def sequential_search(target, lyst):
"""如果找到目标项,返回其索引;否则返回-1"""
position = 0
while position < len(lyst):
if target == lyst[position]:
return position
position += 1
return -1
2.1 最好情况、最坏情况、平均情况
Best-Case, Worst-Case, and Average-Case Performance Revisited
有些算法的性能与数据的排列方式有关,比如顺序搜索算法。此时,我们可以分三种情况考虑考虑该算法的性能:
- 最坏情况:对于"顺序搜索"而言,在最坏情况下,目标项位于列表末尾,或根本不在列表之中。此时必须访问列表中的每一项,对大小为 n 的列表要执行 n 次迭代。因此,顺序搜索在最坏的情况下复杂度为 O(n) 。
- 最好情况:"顺序搜索"只进行一次迭代就在第一个位置找到了目标项,复杂度为 O(1) 。
- 平均情况:需要把从"最好情况"到"最坏情况"间可能出现的所有情况的迭代次数相加,并除以 n。因此,算法平均执行了 (1+2+3+...+n-1+n)/n 次迭代,化简后等于 (n+1)/2 。对于很大的 n 而言,常数因子 2 的作用并不大。因此,平均情况的复杂度仍然为 O(n) 。
3. 二叉搜索
Binary Search
二叉搜索也称二分查找,该算法针对有序列表,其时间复杂度是 O(\log_{2}n) 。
假设我们需要利用二叉搜索查找某个按照升序排列的列表。首先,二叉算法会找出位于列表中间位置的中间项,并将该项与目标项进行比较:如果两者一致,便返回中间项的索引;如果目标项小于中间项,则继续搜索列表的前半部分;反之,则搜索后半部分。当找到目标,或当索引的起点值大于终点值时停止搜索。
注意,使用二叉搜索时有一个额外的整体性代价,就是必须保持列表的有序性。
下面分别使用"循环方式"和"递归方式"来实现二叉搜索。
3.1 循环方式
# -*- coding: utf-8 -*-
def binary_search_loop(sorted_list: list, target: int):
"""
二分查找,循环方式
:param sorted_list: 按升序排列的列表
:param target: 被查找的目标项
:return: 如果sorted_list中包含target,返回target的索引值,否则返回None
"""
low = 0
high = len(sorted_list) - 1
while low <= high:
mid_point = (low + high) // 2
if sorted_list[mid_point] == target:
return mid_point
elif sorted_list[mid_point] > target:
high = mid_point - 1
else:
low = mid_point + 1
return None
if __name__ == '__main__':
my_list = [1, 2, 3, 4]
assert binary_search_loop(my_list, 1) == 1
assert binary_search_loop(my_list, 2) == 1
assert binary_search_loop(my_list, 3) == 2
assert binary_search_loop(my_list, 4) == 3
assert binary_search_loop(my_list, 10) is None
3.2 递归方式
- 基线条件:数组只包含一个元素,如果目标值与该元素相同,便在最终的基线条件下找到了目标值,否则目标值不在数组中。
- 递归条件:每次把数组分成两半,并丢弃其中的一半,对剩下的一半再次执行二分查找。
# -*- coding: utf-8 -*-
def binary_search_recursive(sorted_list: list, target: int):
"""
二分查找,递归方式
:param sorted_list: 按升序排列的列表
:param target: 被查找的目标项
:return: 如果sorted_list中包含target,返回target的索引值,否则返回None
"""
mid = (len(sorted_list) - 1) // 2
if len(sorted_list) == 1: # 基线条件
if target == sorted_list[0]:
return 0
else:
return None
elif target == sorted_list[mid]: # 基线条件
return mid
# 下面的代码,通过递归逐步缩减问题规模
if target > sorted_list[mid]:
index = binary_search_recursive(sorted_list[mid + 1:], target)
if index is None:
return None
# 减半后的新列表sorted_list[mid + 1:]会重新以索引0开头,
# 这里需要保证返回的索引值包含当前sorted_list列表的索引信息,
# 因此需要重新调整index中的索引值。
# 要将index中的索引值调整到sorted_list列表中的对应位置,
# 需要为index加上(mid + 1)
return index + (mid + 1)
else:
index = binary_search_recursive(sorted_list[:mid], target)
return index
if __name__ == '__main__':
assert binary_search_recursive(my_list, 1) == 0
assert binary_search_recursive(my_list, 2) == 1
assert binary_search_recursive(my_list, 3) == 2
assert binary_search_recursive(my_list, 4) == 3
assert binary_search_recursive(my_list, 10) is None
3.3 最坏情况
当目标项不在列表中的时候,便会出现最坏情况。在最坏情况下,对于大小为 n 的列表,会持续将列表长度除以 2,直至商为 1 时停止(如, n//2//...//2 = 1 )——其中除法执行的次数便是循环执行的总次数。假设除法执行的次数为 k ,那么便有 n/2^k=1 ,可得 k=log_2n 。因此,二叉搜索最坏情况的复杂度为 O(log_2n) 。
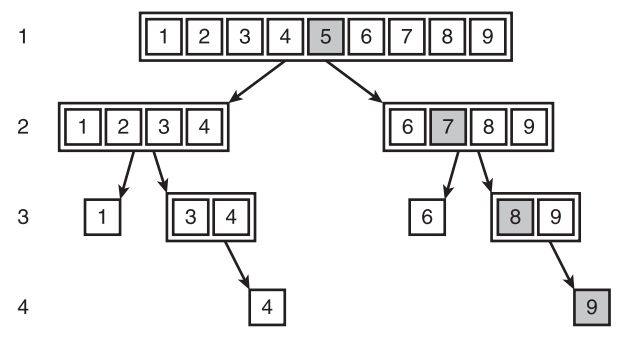
下图展示了在仅含 1~9 的整数列表中,用二叉搜索查找整数 10 的过程。灰色项表示中间项,用于和目标项进行比较,也就是会被访问的项。另外,位于初始列表前半部分的项,实际上并不会被访问。