第五章 相交线与平行线
5.1 相交线
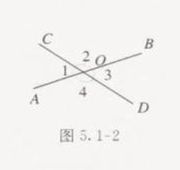
5.1.1 相交线
5.1.2 垂线
在同一平面内,过一点有且只有一条直线与已知直线垂直。
5.1.3 同位角、内错角、同旁内角
5.2 平行线及其判定
5.2.1 平行线
记作a∥b
5.2.2 平行线的判定
1.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行
2.两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行
3.两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行
5.3.1 平行线的性质
1.两条平行线被第三条直线所截,同位角相等
2.两条平行线被第三条直线所截,内错角相等
3.两条平行线被第三条直线所截,同旁内角互补
5.3.2 命题、定理、证明
前面,我们学过一些对某一件事情作出判断的语句,例如:
(1)如果两条直线都与第三条直线平行,那么这两条直线也互相平行
(2)对顶角相等
像这样判断一件事情的语句,叫做命题。命题由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项。
数学中的命题常可以写成“如果....那么.....”的形式,这时“如果”后接的部分是题设,“那么”后接的部分是结论,例如,上面命题(1)中,“两条直线都与第三条直线平行”是题设,“这两条直线也互相平行”是结论。
有些命题的题设和结论不明显,要经过分析才能找到题设和结论,从而将它们写成“如果......那么......”的形式,例如,命题“对顶角相等”可以写成“如果两个角是对顶角,那么这两个角相等”
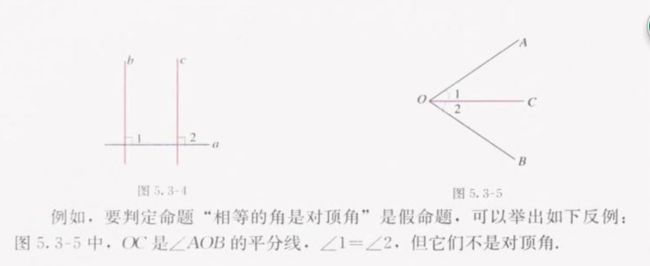
当然有的命题的结论并不正确,这样的命题称为假命题。如果命题成立,就被称为真命题
其中一些真命题是基本事实,是经过反复推理证实的,这样得到的真命题叫做定理。定理也可以作为继续推理的依据。
在很多情况下,一个命题的正确性需要经过推理,才能作出判断,这个推理过程叫做证明。
判定一个命题是假命题,只要举出一个反例,它符合命题的题设,但不满足结论就可以了。
5.4 平移
无重要内容
第六章 实数
实数包括有理数和无理数
6.1 平方根
如果一个数的平方等于9,那么这个数是多少呢?
由于3或-3的平方都是9,因此,如果x²=9,那么x=3或-3
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根。这就是说,如果x²=a,那么x叫做a的平方根。
(注意算数平方根和平方根的区别,算术平方根开出来只有正数)
在我们所认识的数中,任何一个数的平方都不会是负数,所以负数没有平方根。
6.2 立方根
一般地,如果一个数的立方等于a,那么这个数叫做a的立方根或者三次方根,这就是说,如果x³=a,那么x叫做a的立方根
一个数的3分之1次方就可以看作是它的立方根。
6.3 实数
有理数和无理数统称实数。我们可以将学过的数这样分类
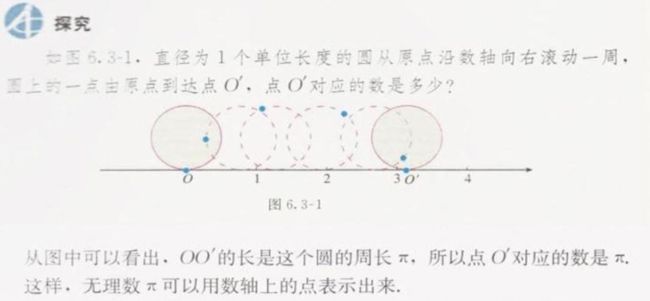
当数的范围扩张到实数后,实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示。
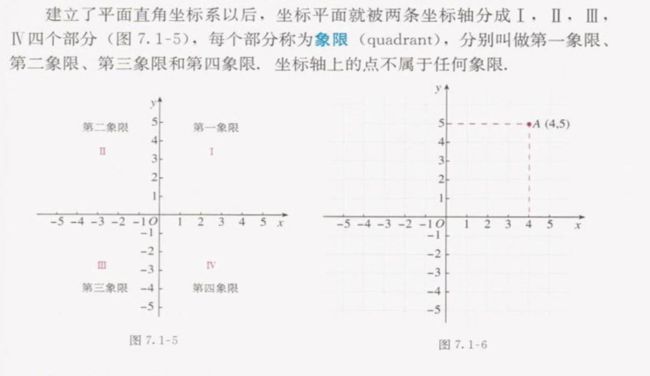
第七章 平面直角坐标系
7.1 平面直角坐标系
7.1.1 有序数对
略
7.1.2 平面直角坐标系
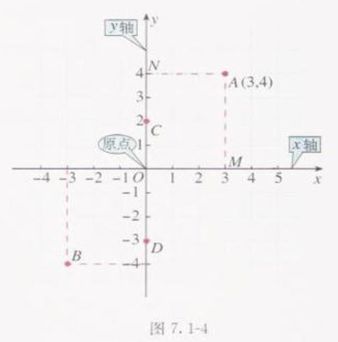
如图7.1-4,我们可以在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系,水平的数轴称为x轴,习惯上取向右为正方向;竖直的数轴称为y轴,取向上方向为正方向;两坐标轴的交点为平面直角坐标系的原点。
7.2 坐标方法的简单应用
7.2.1 用坐标表示地理位置
略
7.2.2 用坐标表示平移
略
第八章 二元一次方程组
8.1 二元一次方程组
每个方程都含有两个未知数(x和y),并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程。
一般地,两元一次方程组的两个方程的公共解,叫做二元一次方程组的解。
8.2 消元-解二元一次方程组
8.3 研究实际问题
解方程很简单,我们的重点应该放在如何根据问题建设起方程
8.4 三元一次方程组的解法
方程组含有三个未知数,每个方程中含未知数的项的次数都是1,并且一共有三个方程,像这样的方程组叫做三元一次方程组。.
而三元一次方程组的思路与二元一次方程组一致。
9.1 不等式
9.1.1 不等式及其解集
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集,求不等式的解集的过程叫做解不等式。
9.1.2 不等式的性质
一般地,不等式有以下性质:
性质1 不等式两边加减同一个数或式子,不等号的方向不变。
性质2 不等式两边乘除同一个正数,不等号的方向不变。
性质3 不等式两边乘除同一个负数,不等号的方向改变。
9.2 一元一次不等式
一元一次不等式依然采用移项来解。但是移项时要以不等式的性质为准。
9.3 一元一次不等式组
和一元一次不等式一致。方程组的解是两个解的重合部分。
第十章 数据的收集、整理与描述
10.1 统计调查
要注意抽样样本必须要保持完全随机性。
10.2 直方图
1.计算最大值与最小值的差
2.决定组距和组数
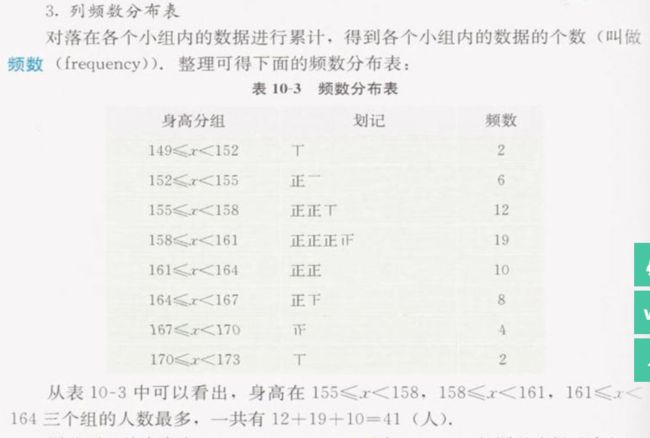
3.列频数分布表