浅谈Apriori算法

emmmm很经典的数据挖掘算法，值得一学。
“`
## 一些基本概念##

1、支持度的定义：support(X–>Y) = |X交Y|/N=集合X与集合Y中的项在一条记录中同时出现的次数/数据记录的个数。
2、自信度的定义：confidence(X–>Y) = |X交Y|/|X| = 集合X与集合Y中的项在一条记录中同时出现的次数/集合X出现的个数。同时满足最小支持度阈值(min_sup)和最小置信度阈值(min_conf)的规则称作强规则 ,如果项集满足最小支持度,则称它为频繁项集。

关联规则的挖掘是一个两步的过程:
1、找出所有频繁项集:根据定义,这些项集出现的频繁性至少和预定义的最小支持计数一样。
2、由频繁项集产生强关联规则:根据定义,这些规则必须满足最小支持度和最小置信度。

## Apriori定律##

Apriori的两条定律是为了尽早的消除一些完全不可能是频繁项集的集合，进而为了减少频繁项集的生成时间。
Apriori定律1：如果一个集合是频繁项集，则它的所有子集都是频繁项集。
Apriori定律2：如果一个集合不是频繁项集，则它的所有超集都不是频繁项集

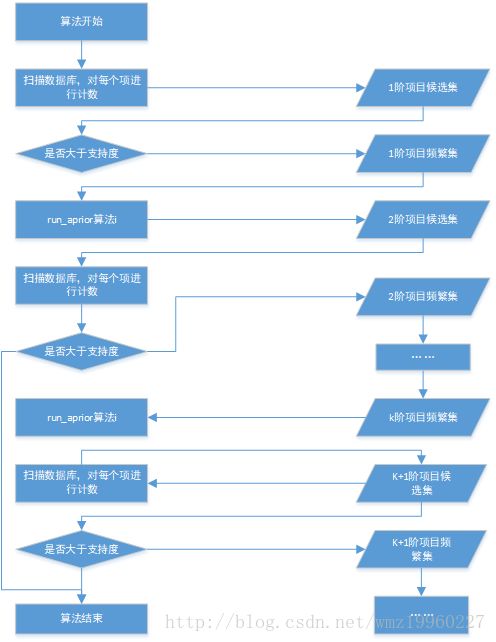
## 实现流程图##

## 具体代码的实现##

# coding=utf-8
from itertools import chain, combinations
from collections import defaultdict


def subsets(arr):
    """ 返回非空子集"""
    return chain(*[combinations(arr, i + 1) for i, a in enumerate(arr)])


def return_item_with_min_support(item_set, transaction_list, min_support, freq_set):
    """
    计算在项集合中的项的支持度
    返回符合最小支持度的子集
   """
    _item_set = set()
    local_set = defaultdict(int)

    for item in item_set:
        for transaction in transaction_list:
            if item.issubset(transaction):
                freq_set[item] += 1
                local_set[item] += 1

    for item, count in local_set.items():
        support = float(count) / len(transaction_list)

        if support >= min_support:
            _item_set.add(item)

    return _item_set


def join_set(item_set, length):
    """
    得到下一阶的候选集
    """
    return set([
        i.union(j)  # 返回一个新的 set 包含 i 和 j 中的每一个元素
        for i in item_set
        for j in item_set if len(i.union(j)) == length
    ])


def getitem_set_transaction_list(data_iterator):
    """
    从数据集中将数据分离
    :param data_iterator:
    :return:
    item_set: 数据集中的所有项
    transaction_list: 所有行(交易)
    """
    transaction_list = list()
    item_set = set()
    for record in data_iterator:
        transaction = frozenset(record)
        transaction_list.append(transaction)
        for item in transaction:
            item_set.add(frozenset([item]))  # Generate 1-item_sets
    return item_set, transaction_list


def run_apriori(data_iter, min_support, min_confidence):
    """
    apriori算法。
    Return
     - 项 (tuple, support)
     - 关联规则 ((pre_tuple, post_tuple), confidence)
    """
    item_set, transaction_list = getitem_set_transaction_list(data_iter)

    freq_set = defaultdict(int)  # 频繁集
    large_set = dict()

    one_c_set = return_item_with_min_support(
        item_set,
        transaction_list,
        min_support,
        freq_set
    )

    current_l_set = one_c_set
    k = 2  # K阶频繁集
    while current_l_set != set([]):
        large_set[k - 1] = current_l_set
        current_l_set = join_set(current_l_set, k)
        current_c_set = return_item_with_min_support(
            current_l_set,
            transaction_list,
            min_support,
            freq_set
        )
        current_l_set = current_c_set
        k = k + 1

    def get_support(item):
        """
        得到每项的支持度
        """
        return float(freq_set[item]) / len(transaction_list)

    # 返回符合最小支持度和可信度的项
    to_ret_items = []
    for key, value in large_set.items():
        to_ret_items.extend(
            [(tuple(item), get_support(item)) for item in value]
        )

    # 返回关联规则
    to_ret_rules = []
    for key, value in large_set.items()[1:]:
        for item in value:
            _subsets = map(frozenset, [x for x in subsets(item)])
            for element in _subsets:
                remain = item.difference(element)
                if len(remain) > 0:
                    confidence = get_support(item) / get_support(element)
                    if confidence >= min_confidence:
                        to_ret_rules.append(
                            ((tuple(element), tuple(remain)), confidence)
                        )
    return to_ret_items, to_ret_rules


def print_results(items, rules):
    """

    打印出按照支持度排列的集合以及按照可信度排列规则
    """
    for item, support in sorted(items, key=lambda (item, support): support):
        print "item: %s , %.3f" % (str(item), support)
    print "\n------------------------ RULES:"
    for rule, confidence in sorted(rules, key=lambda (rule, confidence): confidence):
        pre, post = rule
        print "Rule: %s ==> %s , %.3f" % (str(pre), str(post), confidence)


def data_from_file(fname):
    """
    从文件中读取数据并生成一个生成器
    """
    file_iter = open(fname, 'r')
    for line in file_iter:
        line = line.strip('\n')
        record = frozenset(line.split(' '))
        yield record


if __name__ == "__main__":

    filename = 'test.csv'
    in_file = data_from_file(filename)
    minSupport = 0.1
    minConfidence = 0.7

    re_items, re_rules = run_apriori(in_file, minSupport, minConfidence)
    print_results(re_items, re_rules)

## 运行结果##


## 后记与分析##

Apriori算法是基于大数据挖掘过程的经典算法之一，是一种挖掘布尔型关联规则的频繁项集的迭代算法，该算法需要在数据挖掘过程中通过多次描述数据库来不断寻找候选集，也是可以改进的地方之一，，然后实现剪枝，即除去包含非频繁子集的候选集，。此算法通过对最小支持度阈值的设置，能系统的控制了选项数量的无序增长，并在大数据的数据挖掘过程中产生较大的研究价值。
随着社会的进步，其应用价值也在不断增加，主要包括有：

1. 从海量的学生对教学评价数据中挖掘出关联规则，从而分析出相关课程教学效果与老师教学状态之间的关系；
2. 应用apriori算法可基于网络实现电商交易实时，及时分析出客户消费习惯、消费能力、消费群体，为电商的供应商动态掌握消费市场，并与客户实现良性商务互动提供数据支撑；
3. 应用apriori算法可从人才培养模式中相关的专业、知识体系、从业资格、等海量数据中分析大学生受教育程度和社会就业需求之间的关联性，建立大学生与社会的双向关联性，进一步推动大学为适应社会需求培养人才模式提供准确、客观的数据分析等。