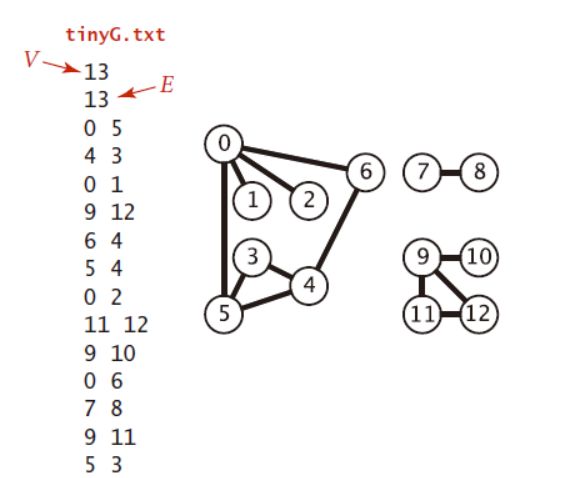
一、无向图
1.1 无向图的定义
边没有方向的图称为无向图。
API定义:
1.2 无向图的抽象表示
1.2.1 邻接矩阵法
使用一个V*V的布尔矩阵表示。当顶点v和顶点w之间有相连接的边时,定义v行w列的元素值为true,否则为false。
特点:现实中的图往往有上百万个顶点,但边的数量很少(稀疏图),V2所需的空间往往不能满足。
源码实现:
public class AdjMatrixGraph {
private int V;
private int E;
private boolean[][] adj;
/*
* Initializes an empty graph with V vertices and 0 edges.
*/
public AdjMatrixGraph(int V) {
this.V = V;
this.E = 0;
this.adj = new boolean[V][V];
}
public void addEdge(int v, int w) {
if (!adj[v][w]) E++;
adj[v][w] = true;
adj[w][v] = true;
}
}
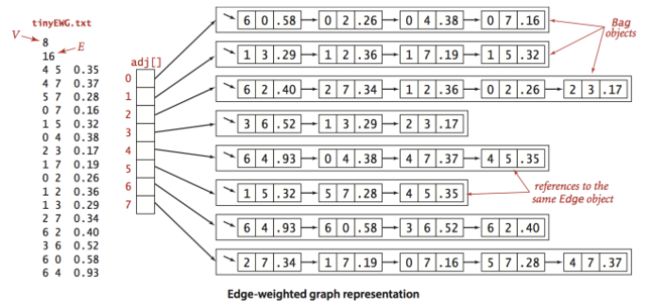
1.2.2 邻接表法
使用一个以顶点为索引的列表数组,数组的每个元素都是和该顶点相邻的顶点列表。
特点:适合稀疏图的表示。节省空间,所需空间与V+E成正比。
1-2-2 无向图的邻接表表示
源码实现:
public class AdjMatrixGraph {
private static final String NEWLINE = System.getProperty("line.separator");
private int V;
private int E;
private boolean[][] adj;
// empty graph with V vertices
public AdjMatrixGraph(int V) {
if (V < 0) throw new RuntimeException("Number of vertices must be nonnegative");
this.V = V;
this.E = 0;
this.adj = new boolean[V][V];
}
// random graph with V vertices and E edges
public AdjMatrixGraph(int V, int E) {
this(V);
if (E < 0) throw new RuntimeException("Number of edges must be nonnegative");
if (E > V*(V-1) + V) throw new RuntimeException("Too many edges");
// can be inefficient
while (this.E != E) {
int v = StdRandom.uniform(V);
int w = StdRandom.uniform(V);
addEdge(v, w);
}
}
// number of vertices and edges
public int V() { return V; }
public int E() { return E; }
// add undirected edge v-w
public void addEdge(int v, int w) {
if (!adj[v][w]) E++;
adj[v][w] = true;
adj[w][v] = true;
}
// does the graph contain the edge v-w?
public boolean contains(int v, int w) {
return adj[v][w];
}
// return list of neighbors of v
public Iterable adj(int v) {
return new AdjIterator(v);
}
// support iteration over graph vertices
private class AdjIterator implements Iterator, Iterable {
private int v;
private int w = 0;
AdjIterator(int v) {
this.v = v;
}
public Iterator iterator() {
return this;
}
public boolean hasNext() {
while (w < V) {
if (adj[v][w]) return true;
w++;
}
return false;
}
public Integer next() {
if (!hasNext()) {
throw new NoSuchElementException();
}
return w++;
}
public void remove() {
throw new UnsupportedOperationException();
}
}
// string representation of Graph - takes quadratic time
public String toString() {
StringBuilder s = new StringBuilder();
s.append(V + " " + E + NEWLINE);
for (int v = 0; v < V; v++) {
s.append(v + ": ");
for (int w : adj(v)) {
s.append(w + " ");
}
s.append(NEWLINE);
}
return s.toString();
}
// test client
public static void main(String[] args) {
int V = Integer.parseInt(args[0]);
int E = Integer.parseInt(args[1]);
AdjMatrixGraph G = new AdjMatrixGraph(V, E);
StdOut.println(G);
}
}
二、有向图
2.1 有向图的定义
边有方向的图称为有向图。
2-1 有向图示例
API定义:
2.2 有向图的抽象表示
有向图和无向图一样既可以用邻接表法实现,也可以用邻接矩阵法实现。
本文只给出邻接表的实现方法。
2.2.1 邻接表法
源码实现:
public class Digraph {
private static final String NEWLINE = System.getProperty("line.separator");
private final int V; // number of vertices in this digraph
private int E; // number of edges in this digraph
private Bag[] adj; // adj[v] = adjacency list for vertex v
private int[] indegree; // indegree[v] = indegree of vertex v
/**
* Initializes an empty digraph with V vertices.
*
* @param V the number of vertices
* @throws IllegalArgumentException if {@code V < 0}
*/
public Digraph(int V) {
if (V < 0) throw new IllegalArgumentException("Number of vertices in a Digraph must be nonnegative");
this.V = V;
this.E = 0;
indegree = new int[V];
adj = (Bag[]) new Bag[V];
for (int v = 0; v < V; v++) {
adj[v] = new Bag();
}
}
/**
* Initializes a digraph from the specified input stream.
* The format is the number of vertices V,
* followed by the number of edges E,
* followed by E pairs of vertices, with each entry separated by whitespace.
*
* @param in the input stream
* @throws IllegalArgumentException if the endpoints of any edge are not in prescribed range
* @throws IllegalArgumentException if the number of vertices or edges is negative
* @throws IllegalArgumentException if the input stream is in the wrong format
*/
public Digraph(In in) {
try {
this.V = in.readInt();
if (V < 0) throw new IllegalArgumentException("number of vertices in a Digraph must be nonnegative");
indegree = new int[V];
adj = (Bag[]) new Bag[V];
for (int v = 0; v < V; v++) {
adj[v] = new Bag();
}
int E = in.readInt();
if (E < 0) throw new IllegalArgumentException("number of edges in a Digraph must be nonnegative");
for (int i = 0; i < E; i++) {
int v = in.readInt();
int w = in.readInt();
addEdge(v, w);
}
}
catch (NoSuchElementException e) {
throw new IllegalArgumentException("invalid input format in Digraph constructor", e);
}
}
/**
* Initializes a new digraph that is a deep copy of the specified digraph.
*
* @param G the digraph to copy
*/
public Digraph(Digraph G) {
this(G.V());
this.E = G.E();
for (int v = 0; v < V; v++)
this.indegree[v] = G.indegree(v);
for (int v = 0; v < G.V(); v++) {
// reverse so that adjacency list is in same order as original
Stack reverse = new Stack();
for (int w : G.adj[v]) {
reverse.push(w);
}
for (int w : reverse) {
adj[v].add(w);
}
}
}
/**
* Returns the number of vertices in this digraph.
*
* @return the number of vertices in this digraph
*/
public int V() {
return V;
}
/**
* Returns the number of edges in this digraph.
*
* @return the number of edges in this digraph
*/
public int E() {
return E;
}
// throw an IllegalArgumentException unless {@code 0 <= v < V}
private void validateVertex(int v) {
if (v < 0 || v >= V)
throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
}
/**
* Adds the directed edge v鈫抴 to this digraph.
*
* @param v the tail vertex
* @param w the head vertex
* @throws IllegalArgumentException unless both {@code 0 <= v < V} and {@code 0 <= w < V}
*/
public void addEdge(int v, int w) {
validateVertex(v);
validateVertex(w);
adj[v].add(w);
indegree[w]++;
E++;
}
/**
* Returns the vertices adjacent from vertex {@code v} in this digraph.
*
* @param v the vertex
* @return the vertices adjacent from vertex {@code v} in this digraph, as an iterable
* @throws IllegalArgumentException unless {@code 0 <= v < V}
*/
public Iterable adj(int v) {
validateVertex(v);
return adj[v];
}
/**
* Returns the number of directed edges incident from vertex {@code v}.
* This is known as the outdegree of vertex {@code v}.
*
* @param v the vertex
* @return the outdegree of vertex {@code v}
* @throws IllegalArgumentException unless {@code 0 <= v < V}
*/
public int outdegree(int v) {
validateVertex(v);
return adj[v].size();
}
/**
* Returns the number of directed edges incident to vertex {@code v}.
* This is known as the indegree of vertex {@code v}.
*
* @param v the vertex
* @return the indegree of vertex {@code v}
* @throws IllegalArgumentException unless {@code 0 <= v < V}
*/
public int indegree(int v) {
validateVertex(v);
return indegree[v];
}
/**
* Returns the reverse of the digraph.
*
* @return the reverse of the digraph
*/
public Digraph reverse() {
Digraph reverse = new Digraph(V);
for (int v = 0; v < V; v++) {
for (int w : adj(v)) {
reverse.addEdge(w, v);
}
}
return reverse;
}
/**
* Returns a string representation of the graph.
*
* @return the number of vertices V, followed by the number of edges E,
* followed by the V adjacency lists
*/
public String toString() {
StringBuilder s = new StringBuilder();
s.append(V + " vertices, " + E + " edges " + NEWLINE);
for (int v = 0; v < V; v++) {
s.append(String.format("%d: ", v));
for (int w : adj[v]) {
s.append(String.format("%d ", w));
}
s.append(NEWLINE);
}
return s.toString();
}
/**
* Unit tests the {@code Digraph} data type.
*
* @param args the command-line arguments
*/
public static void main(String[] args) {
In in = new In(args[0]);
Digraph G = new Digraph(in);
StdOut.println(G);
}
}
三、加权无向图
3.1 加权无向图的定义
加权无向图就是边带权重值得无向图。
API定义:
3-1-2 加权无向图边的API
3.2 加权无向图的抽象表示
3.2.1 邻接表法
边-源码实现:
public class Edge implements Comparable {
private final int v;
private final int w;
private final double weight;
/**
* Initializes an edge between vertices {@code v} and {@code w} of
* the given {@code weight}.
*
* @param v one vertex
* @param w the other vertex
* @param weight the weight of this edge
* @throws IllegalArgumentException if either {@code v} or {@code w}
* is a negative integer
* @throws IllegalArgumentException if {@code weight} is {@code NaN}
*/
public Edge(int v, int w, double weight) {
if (v < 0) throw new IllegalArgumentException("vertex index must be a nonnegative integer");
if (w < 0) throw new IllegalArgumentException("vertex index must be a nonnegative integer");
if (Double.isNaN(weight)) throw new IllegalArgumentException("Weight is NaN");
this.v = v;
this.w = w;
this.weight = weight;
}
/**
* Returns the weight of this edge.
*
* @return the weight of this edge
*/
public double weight() {
return weight;
}
/**
* Returns either endpoint of this edge.
*
* @return either endpoint of this edge
*/
public int either() {
return v;
}
/**
* Returns the endpoint of this edge that is different from the given vertex.
*
* @param vertex one endpoint of this edge
* @return the other endpoint of this edge
* @throws IllegalArgumentException if the vertex is not one of the
* endpoints of this edge
*/
public int other(int vertex) {
if (vertex == v) return w;
else if (vertex == w) return v;
else throw new IllegalArgumentException("Illegal endpoint");
}
/**
* Compares two edges by weight.
* Note that {@code compareTo()} is not consistent with {@code equals()},
* which uses the reference equality implementation inherited from {@code Object}.
*
* @param that the other edge
* @return a negative integer, zero, or positive integer depending on whether
* the weight of this is less than, equal to, or greater than the
* argument edge
*/
@Override
public int compareTo(Edge that) {
return Double.compare(this.weight, that.weight);
}
/**
* Returns a string representation of this edge.
*
* @return a string representation of this edge
*/
public String toString() {
return String.format("%d-%d %.5f", v, w, weight);
}
/**
* Unit tests the {@code Edge} data type.
*
* @param args the command-line arguments
*/
public static void main(String[] args) {
Edge e = new Edge(12, 34, 5.67);
StdOut.println(e);
}
}
加权无向图-源码实现:
public class EdgeWeightedGraph {
private static final String NEWLINE = System.getProperty("line.separator");
private final int V;
private int E;
private Bag[] adj;
/**
* Initializes an empty edge-weighted graph with {@code V} vertices and 0 edges.
*
* @param V the number of vertices
* @throws IllegalArgumentException if {@code V < 0}
*/
public EdgeWeightedGraph(int V) {
if (V < 0) throw new IllegalArgumentException("Number of vertices must be nonnegative");
this.V = V;
this.E = 0;
adj = (Bag[]) new Bag[V];
for (int v = 0; v < V; v++) {
adj[v] = new Bag();
}
}
/**
* Initializes a random edge-weighted graph with {@code V} vertices and E edges.
*
* @param V the number of vertices
* @param E the number of edges
* @throws IllegalArgumentException if {@code V < 0}
* @throws IllegalArgumentException if {@code E < 0}
*/
public EdgeWeightedGraph(int V, int E) {
this(V);
if (E < 0) throw new IllegalArgumentException("Number of edges must be nonnegative");
for (int i = 0; i < E; i++) {
int v = StdRandom.uniform(V);
int w = StdRandom.uniform(V);
double weight = Math.round(100 * StdRandom.uniform()) / 100.0;
Edge e = new Edge(v, w, weight);
addEdge(e);
}
}
/**
* Initializes an edge-weighted graph from an input stream.
* The format is the number of vertices V,
* followed by the number of edges E,
* followed by E pairs of vertices and edge weights,
* with each entry separated by whitespace.
*
* @param in the input stream
* @throws IllegalArgumentException if the endpoints of any edge are not in prescribed range
* @throws IllegalArgumentException if the number of vertices or edges is negative
*/
public EdgeWeightedGraph(In in) {
this(in.readInt());
int E = in.readInt();
if (E < 0) throw new IllegalArgumentException("Number of edges must be nonnegative");
for (int i = 0; i < E; i++) {
int v = in.readInt();
int w = in.readInt();
validateVertex(v);
validateVertex(w);
double weight = in.readDouble();
Edge e = new Edge(v, w, weight);
addEdge(e);
}
}
/**
* Initializes a new edge-weighted graph that is a deep copy of {@code G}.
*
* @param G the edge-weighted graph to copy
*/
public EdgeWeightedGraph(EdgeWeightedGraph G) {
this(G.V());
this.E = G.E();
for (int v = 0; v < G.V(); v++) {
// reverse so that adjacency list is in same order as original
Stack reverse = new Stack();
for (Edge e : G.adj[v]) {
reverse.push(e);
}
for (Edge e : reverse) {
adj[v].add(e);
}
}
}
/**
* Returns the number of vertices in this edge-weighted graph.
*
* @return the number of vertices in this edge-weighted graph
*/
public int V() {
return V;
}
/**
* Returns the number of edges in this edge-weighted graph.
*
* @return the number of edges in this edge-weighted graph
*/
public int E() {
return E;
}
// throw an IllegalArgumentException unless {@code 0 <= v < V}
private void validateVertex(int v) {
if (v < 0 || v >= V)
throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
}
/**
* Adds the undirected edge {@code e} to this edge-weighted graph.
*
* @param e the edge
* @throws IllegalArgumentException unless both endpoints are between {@code 0} and {@code V-1}
*/
public void addEdge(Edge e) {
int v = e.either();
int w = e.other(v);
validateVertex(v);
validateVertex(w);
adj[v].add(e);
adj[w].add(e);
E++;
}
/**
* Returns the edges incident on vertex {@code v}.
*
* @param v the vertex
* @return the edges incident on vertex {@code v} as an Iterable
* @throws IllegalArgumentException unless {@code 0 <= v < V}
*/
public Iterable adj(int v) {
validateVertex(v);
return adj[v];
}
/**
* Returns the degree of vertex {@code v}.
*
* @param v the vertex
* @return the degree of vertex {@code v}
* @throws IllegalArgumentException unless {@code 0 <= v < V}
*/
public int degree(int v) {
validateVertex(v);
return adj[v].size();
}
/**
* Returns all edges in this edge-weighted graph.
* To iterate over the edges in this edge-weighted graph, use foreach notation:
* {@code for (Edge e : G.edges())}.
*
* @return all edges in this edge-weighted graph, as an iterable
*/
public Iterable edges() {
Bag list = new Bag();
for (int v = 0; v < V; v++) {
int selfLoops = 0;
for (Edge e : adj(v)) {
if (e.other(v) > v) {
list.add(e);
}
// add only one copy of each self loop (self loops will be consecutive)
else if (e.other(v) == v) {
if (selfLoops % 2 == 0) list.add(e);
selfLoops++;
}
}
}
return list;
}
/**
* Returns a string representation of the edge-weighted graph.
* This method takes time proportional to E + V.
*
* @return the number of vertices V, followed by the number of edges E,
* followed by the V adjacency lists of edges
*/
public String toString() {
StringBuilder s = new StringBuilder();
s.append(V + " " + E + NEWLINE);
for (int v = 0; v < V; v++) {
s.append(v + ": ");
for (Edge e : adj[v]) {
s.append(e + " ");
}
s.append(NEWLINE);
}
return s.toString();
}
/**
* Unit tests the {@code EdgeWeightedGraph} data type.
*
* @param args the command-line arguments
*/
public static void main(String[] args) {
In in = new In(args[0]);
EdgeWeightedGraph G = new EdgeWeightedGraph(in);
StdOut.println(G);
}
}
四、加权有向图
4.1 加权有向图的定义
加权有向图就是边带权重值的有向图。
API定义:
4-1-2 加权有向图的边的API定义
4.2 加权有向图的抽象表示
4.2.1 邻接表法
4-2-1 加权有向图的邻接表表示
边-源码实现:
public class DirectedEdge {
private final int v;
private final int w;
private final double weight;
/**
* Initializes a directed edge from vertex {@code v} to vertex {@code w} with
* the given {@code weight}.
* @param v the tail vertex
* @param w the head vertex
* @param weight the weight of the directed edge
* @throws IllegalArgumentException if either {@code v} or {@code w}
* is a negative integer
* @throws IllegalArgumentException if {@code weight} is {@code NaN}
*/
public DirectedEdge(int v, int w, double weight) {
if (v < 0) throw new IllegalArgumentException("Vertex names must be nonnegative integers");
if (w < 0) throw new IllegalArgumentException("Vertex names must be nonnegative integers");
if (Double.isNaN(weight)) throw new IllegalArgumentException("Weight is NaN");
this.v = v;
this.w = w;
this.weight = weight;
}
/**
* Returns the tail vertex of the directed edge.
* @return the tail vertex of the directed edge
*/
public int from() {
return v;
}
/**
* Returns the head vertex of the directed edge.
* @return the head vertex of the directed edge
*/
public int to() {
return w;
}
/**
* Returns the weight of the directed edge.
* @return the weight of the directed edge
*/
public double weight() {
return weight;
}
/**
* Returns a string representation of the directed edge.
* @return a string representation of the directed edge
*/
public String toString() {
return v + "->" + w + " " + String.format("%5.2f", weight);
}
/**
* Unit tests the {@code DirectedEdge} data type.
*
* @param args the command-line arguments
*/
public static void main(String[] args) {
DirectedEdge e = new DirectedEdge(12, 34, 5.67);
StdOut.println(e);
}
}
加权有向图-源码实现:
public class EdgeWeightedDigraph {
private static final String NEWLINE = System.getProperty("line.separator");
private final int V; // number of vertices in this digraph
private int E; // number of edges in this digraph
private Bag[] adj; // adj[v] = adjacency list for vertex v
private int[] indegree; // indegree[v] = indegree of vertex v
/**
* Initializes an empty edge-weighted digraph with {@code V} vertices and 0 edges.
*
* @param V the number of vertices
* @throws IllegalArgumentException if {@code V < 0}
*/
public EdgeWeightedDigraph(int V) {
if (V < 0) throw new IllegalArgumentException("Number of vertices in a Digraph must be nonnegative");
this.V = V;
this.E = 0;
this.indegree = new int[V];
adj = (Bag[]) new Bag[V];
for (int v = 0; v < V; v++)
adj[v] = new Bag();
}
/**
* Initializes a random edge-weighted digraph with {@code V} vertices and E edges.
*
* @param V the number of vertices
* @param E the number of edges
* @throws IllegalArgumentException if {@code V < 0}
* @throws IllegalArgumentException if {@code E < 0}
*/
public EdgeWeightedDigraph(int V, int E) {
this(V);
if (E < 0) throw new IllegalArgumentException("Number of edges in a Digraph must be nonnegative");
for (int i = 0; i < E; i++) {
int v = StdRandom.uniform(V);
int w = StdRandom.uniform(V);
double weight = 0.01 * StdRandom.uniform(100);
DirectedEdge e = new DirectedEdge(v, w, weight);
addEdge(e);
}
}
/**
* Initializes an edge-weighted digraph from the specified input stream.
* The format is the number of vertices V,
* followed by the number of edges E,
* followed by E pairs of vertices and edge weights,
* with each entry separated by whitespace.
*
* @param in the input stream
* @throws IllegalArgumentException if the endpoints of any edge are not in prescribed range
* @throws IllegalArgumentException if the number of vertices or edges is negative
*/
public EdgeWeightedDigraph(In in) {
this(in.readInt());
int E = in.readInt();
if (E < 0) throw new IllegalArgumentException("Number of edges must be nonnegative");
for (int i = 0; i < E; i++) {
int v = in.readInt();
int w = in.readInt();
validateVertex(v);
validateVertex(w);
double weight = in.readDouble();
addEdge(new DirectedEdge(v, w, weight));
}
}
/**
* Initializes a new edge-weighted digraph that is a deep copy of {@code G}.
*
* @param G the edge-weighted digraph to copy
*/
public EdgeWeightedDigraph(EdgeWeightedDigraph G) {
this(G.V());
this.E = G.E();
for (int v = 0; v < G.V(); v++)
this.indegree[v] = G.indegree(v);
for (int v = 0; v < G.V(); v++) {
// reverse so that adjacency list is in same order as original
Stack reverse = new Stack();
for (DirectedEdge e : G.adj[v]) {
reverse.push(e);
}
for (DirectedEdge e : reverse) {
adj[v].add(e);
}
}
}
/**
* Returns the number of vertices in this edge-weighted digraph.
*
* @return the number of vertices in this edge-weighted digraph
*/
public int V() {
return V;
}
/**
* Returns the number of edges in this edge-weighted digraph.
*
* @return the number of edges in this edge-weighted digraph
*/
public int E() {
return E;
}
// throw an IllegalArgumentException unless {@code 0 <= v < V}
private void validateVertex(int v) {
if (v < 0 || v >= V)
throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
}
/**
* Adds the directed edge {@code e} to this edge-weighted digraph.
*
* @param e the edge
* @throws IllegalArgumentException unless endpoints of edge are between {@code 0}
* and {@code V-1}
*/
public void addEdge(DirectedEdge e) {
int v = e.from();
int w = e.to();
validateVertex(v);
validateVertex(w);
adj[v].add(e);
indegree[w]++;
E++;
}
/**
* Returns the directed edges incident from vertex {@code v}.
*
* @param v the vertex
* @return the directed edges incident from vertex {@code v} as an Iterable
* @throws IllegalArgumentException unless {@code 0 <= v < V}
*/
public Iterable adj(int v) {
validateVertex(v);
return adj[v];
}
/**
* Returns the number of directed edges incident from vertex {@code v}.
* This is known as the outdegree of vertex {@code v}.
*
* @param v the vertex
* @return the outdegree of vertex {@code v}
* @throws IllegalArgumentException unless {@code 0 <= v < V}
*/
public int outdegree(int v) {
validateVertex(v);
return adj[v].size();
}
/**
* Returns the number of directed edges incident to vertex {@code v}.
* This is known as the indegree of vertex {@code v}.
*
* @param v the vertex
* @return the indegree of vertex {@code v}
* @throws IllegalArgumentException unless {@code 0 <= v < V}
*/
public int indegree(int v) {
validateVertex(v);
return indegree[v];
}
/**
* Returns all directed edges in this edge-weighted digraph.
* To iterate over the edges in this edge-weighted digraph, use foreach notation:
* {@code for (DirectedEdge e : G.edges())}.
*
* @return all edges in this edge-weighted digraph, as an iterable
*/
public Iterable edges() {
Bag list = new Bag();
for (int v = 0; v < V; v++) {
for (DirectedEdge e : adj(v)) {
list.add(e);
}
}
return list;
}
/**
* Returns a string representation of this edge-weighted digraph.
*
* @return the number of vertices V, followed by the number of edges E,
* followed by the V adjacency lists of edges
*/
public String toString() {
StringBuilder s = new StringBuilder();
s.append(V + " " + E + NEWLINE);
for (int v = 0; v < V; v++) {
s.append(v + ": ");
for (DirectedEdge e : adj[v]) {
s.append(e + " ");
}
s.append(NEWLINE);
}
return s.toString();
}
/**
* Unit tests the {@code EdgeWeightedDigraph} data type.
*
* @param args the command-line arguments
*/
public static void main(String[] args) {
In in = new In(args[0]);
EdgeWeightedDigraph G = new EdgeWeightedDigraph(in);
StdOut.println(G);
}
}