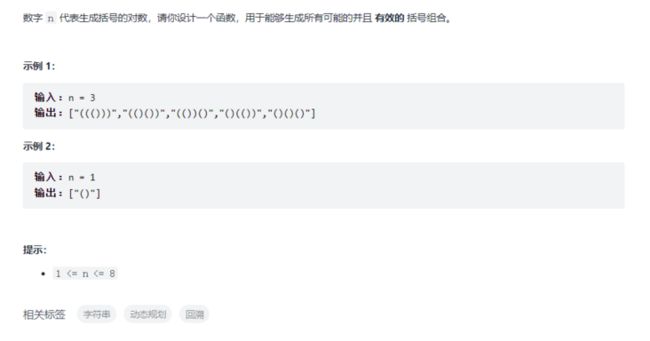
第一题 括号生成
题目
动态规划解法
我们可以将括号的生成看作
不断的在括号对中加入新的括号
这样对于n对括号的生成 我们便能在n-1对括号中进行操作

参考
https://leetcode-cn.com/probl...
https://leetcode-cn.com/probl...
java版本
递归实现
// 9ms
public List generateParenthesis(int n) {
List res = new LinkedList<>();
if (n == 0) {
res.add("");
return res;
}
for (int i = 0; i < n; i++) {
int j = n - i - 1;
List iRes = generateParenthesis(i);
List jRes = generateParenthesis(j);
for (String s1 : iRes) {
for (String s2 : jRes) {
res.add(s1 + "(" + s2 + ")");
}
}
}
return res;
}
作者:fan-lu-5
链接:https://leetcode-cn.com/problems/generate-parentheses/solution/java-0ms-cong-zhao-gui-lu-dao-xuan-ding-2qm9t/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。 将小于n的计算结果存储起来供后续计算使用,减少重复计算
// 8ms
public List generateParenthesis(int n) {
Map> mem = new HashMap<>();
return dp(n, mem);
}
private List dp(int n, Map> mem) {
if (mem.containsKey(n))
return mem.get(n);
List res = new LinkedList<>();
if (n == 0) {
res.add("");
return res;
}
for (int i = 0; i < n; i++) {
int j = n - i - 1;
List iRes = dp(i, mem);
List jRes = dp(j, mem);
for (String s1 : iRes) {
for (String s2 : jRes) {
res.add(s1 + "(" + s2 + ")");
}
}
}
mem.put(n, res);
return res;
}
作者:fan-lu-5
链接:https://leetcode-cn.com/problems/generate-parentheses/solution/java-0ms-cong-zhao-gui-lu-dao-xuan-ding-2qm9t/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。 go版本
递归实现
func generateParenthesis(n int) []string {
var res []string
if n == 0 {
res=append(res,"")
return res
}
//i从0到n-1 j从n-1到0
for i := 0; i < n; i++ {
j := n - i - 1
//生成i和j的括号序列
iRes := generateParenthesis(i)
jRes := generateParenthesis(j)
for _,s1:=range iRes {
for _,s2:=range jRes {
res=append(res,s1 + "(" + s2 + ")")
}
}
}
return res
}加入存储
func generateParenthesis(n int) []string {
var mem map[int][]string
//如果没有对mem进行初始化,只进行声明 那么mem默认为nil
//在对mem进行赋值操作时会抛出一个panic异常
mem = make(map[int][]string)
return dp(n, mem)
}
func dp(n int, mem map[int][]string) []string {
if value, ok := mem[n];ok{
return value
}
var res []string
if n == 0 {
res=append(res,"")
return res
}
for i := 0; i < n; i++ {
j := n - i - 1
iRes := dp(i, mem)
jRes := dp(j, mem)
for _,s1:=range iRes {
for _,s2:=range jRes {
res=append(res,s1 + "(" + s2 + ")")
}
}
}
mem[n]=res
return res
}官解 从暴力到回溯
暴力解法
func generateParenthesis(n int) []string {
var combinations []string
num := make([]byte, 2*n)
generateAll(&num, 0,&combinations)
return combinations
}
func generateAll(current *[]byte, pos int, result *[]string) {
if pos == len(*current) {
if valid(*current) {
*result = append(*result, string(*current))
}
} else {
(*current)[pos] = '('
generateAll(current, pos+1, result)
(*current)[pos] = ')'
generateAll(current, pos+1, result)
}
}
func valid(current []byte) bool {
balance := 0
for _,c := range current {
if c == '(' {
balance++
} else {
balance--
}
if balance < 0 {
return false
}
}
return balance == 0
}func generateParenthesis(n int) []string {
res = []string{}
run([]byte{}, 2 * n)
return res
}
var res []string
func run(cur []byte, n int) {
if n == 0 {
if isValid(cur) {
res = append(res, string(cur))
}
return
}
tpl := []byte{'(', ')'}
for i := 0; i < len(tpl); i++ {
cur = append(cur, tpl[i])
run(cur, n - 1)
cur = cur[:len(cur)-1]
}
}
func isValid(cur []byte) bool {
var st []byte
for i := 0; i < len(cur); i++ {
if cur[i] == '(' {
st = append(st, cur[i])
continue
}
if len(st) == 0 {
return false
}
st = st[:len(st)-1]
}
return len(st) == 0
}
作者:dfzhou6
链接:https://leetcode-cn.com/problems/generate-parentheses/solution/jian-dan-yi-dong-go-by-dfzhou6-frkl/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。第二题 全排列
题目
递归
每次在nums中挑出一个数作为第一个数,剩下的数进行排列之后放在第一个数后面
剩下的数又可以调用该函数继续完成全排列
重复n次,就完成了所有可能性的组合
代码
func permute(nums []int) [][]int {
var res [][]int
if len(nums) == 0 {
return res
}
var n []int
if len(nums) == 1 {
n = append(n, nums[0])
res = append(res, n)
}
for i := 0; i < len(nums); i++ {
n = append(n, nums[i])
co :=make([]int,len(nums))
copy(co, nums)
co[0], co[i] = co[i], co[0]
pers := permute(co[1:])
for _, per := range pers {
nn := append(n, per...)
res = append(res, nn)
}
n = nil
}
return res
}结果
虽然递归的时间复杂度比较快,但在数量级比较高的时候递归调用栈使用的空间会比较大
回溯法
https://leetcode-cn.com/probl...
var res [][]int
func permute(nums []int) [][]int {
res = [][]int{}
backTrack(nums,len(nums),[]int{})
return res
}
func backTrack(nums []int,numsLen int,path []int) {
if len(nums)==0{
p:=make([]int,len(path))
copy(p,path)
res = append(res,p)
}
for i:=0;i