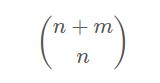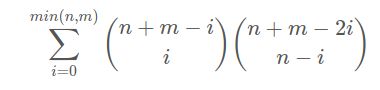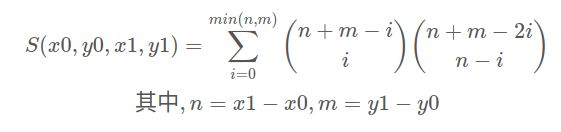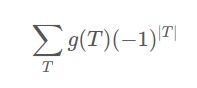大家周末好。今天给大家分享两个题,正好这两个题涉及到的知识点很多,但是很精彩,可能要看很久,可以周末慢慢看。题目分别是马拦过河卒和马拦过河卒2。涉及到动态规划以及组合数学的很多知识点。
其中第一题,标准的马拦过河卒问题是入门的棋盘 DP 的题目,非常基础。
如果没有马拦着过河卒,那么 leetcode 上有一样的题目,62. 不同路径。
有马拦着过河卒,则棋盘上会有一些点是障碍点,leetcode 上也有类似的题,63. 不同路径 II,只是障碍点不是通过马脚的方式给出。
但是本文的第二题,也就是马拦过河卒的变形题就复杂很多了,首先卒除了横着竖着走,还可以斜着走,其次是棋盘的长和宽很大,障碍点个数在 20 个以内,可以套棋盘 DP,但是 O(nm) 的时间复杂的不允许。只能从障碍点 20 个以内入手,通过组合数学解决。
本题是组合数学的一道好题,基本上把组合数学的常见知识点都过了一遍,涉及到组合计数,容斥计数,组合枚举,卢卡斯定理。当然有一些内容是稍微超纲的,但是对于工程师来说,找一些资料学习一下之后应该不难理解。
有的朋友如果之前没有学过组合数学的话,第二题会需要看比较长的时间,可以收藏一下周末慢慢看。
下面是解决第二题涉及到的组合数学的知识点,链接中是我写的知识梳理,以及代码模板。
组合计数: 针对可以斜线走的情况正确计数, 这块可以参考下面这篇文章
文章: 组合数学1-排列组合
链接: https://chengzhaoxi.xyz/64534.html
容斥计数: 主要涉及 N 个集合的容斥如何实现,这块可以参考下面这篇文章。
文章: 容斥计数
链接: https://chengzhaoxi.xyz/65b49d4d.html
组合枚举: 枚举所有可能同时出现在一条路径上的障碍点的时候,涉及到对组合的枚举,这块可以参考下面这篇文章 枚举。
文章: 枚举
链接: https://chengzhaoxi.xyz/17699.html
卢卡斯定理: 涉及到用求n, m 很大时的大组合数模质数的问题,这块可以参考下面这篇文章。
文章: 组合数
链接: https://chengzhaoxi.xyz/40979.html
下面我们就分别看这两个题。这两个题都是洛谷上的,如果想提交代码的话可以在洛谷上搜卒这个关键字即可。注意第一题是非常基础的动态规划的题目,如果这个题有问题的话,需要补一下动态规划这块。第二题如果没学过组合数学的话不会很正常,可以欣赏为主,顺便学习一些排列组合,容斥及其实现方法。
马拦过河卒1
棋盘上 A 点有一个过河卒,需要走到目标 B 点。卒行走的规则:可以向下、或者向右。同时在棋盘上 C 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示,A 点 (0, 0)(0,0)、B 点 (n, m)(n,m),同样马的位置坐标是需要给出的。
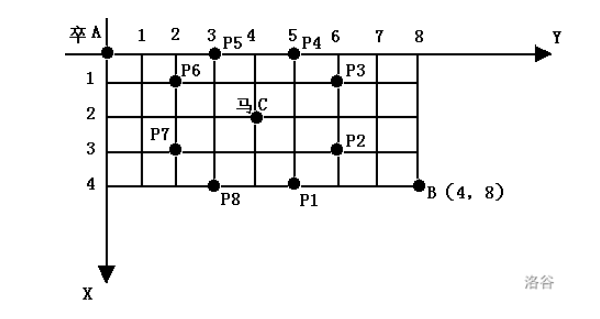
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
1
2
3
4
5
6
7
8
|
输入格式
一行四个正整数,分别表示 B 点坐标和马的坐标。
输出格式
一个整数,表示所有的路径条数。
说明
1 <= n, m <= 20, 0 <= 马的坐标 <= 20。
|
输入输出样例
输入
6 6 3 3
输出
6
算法: 动态规划
棋盘DP算法
1
2
3
4
5
6
7
8
9
10
11
12
|
状态定义
dp[i][j] := 从 (i, j) 到 (n, m) 的方法数
答案
dp[0][0]
初始化
dp[n][m] = 1
dp[i][j] = 0, 若 (i, j) 为马脚
状态转移
dp[i][j] = dp[i + 1][j] + dp[i][j + 1]
|
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
#include
#include
using namespace std;
using ll = long long;
void init(vector>& dp, int x0, int y0, int n, int m)
{
dp[n][m] = 1;
dp[x0][y0] = 0;
int dx[8] = {1, 1, 2, 2, -1, -1, -2, -2};
int dy[8] = {2, -2, 1, -1, 2, -2, 1, -1};
for(int d = 0; d < 8; ++d)
{
int x = x0 + dx[d];
int y = y0 + dy[d];
if(x >= 0 && y >= 0 && x <= n && y <= m)
dp[x][y] = 0;
}
}
ll solve(int i, int j, const int n, const int m, vector>& dp)
{
if(dp[i][j] != -1)
return dp[i][j];
ll ans = 0;
if(i + 1 <= n)
ans += solve(i + 1, j, n, m, dp);
if(j + 1 <= m)
ans += solve(i, j + 1, n, m, dp);
return dp[i][j] = ans;
}
int main()
{
int n, m, x0, y0;
cin >> n >> m >> x0 >> y0;
vector> dp(n + 1, vector(m + 1, -1));
init(dp, x0, y0, n, m);
ll ans = solve(0, 0, n, m, dp);
cout << ans << endl;
}
|
马拦过河卒2
卒的起点为左下角的 (1, 1) 目标是走到右上角的 (n, m),求方案数,模 59393。
有 K 个坐标是卒不能走的
当前点为 (x, y) 时,每步可以选择都走法为 (x + 1, y), (x, y + 1), (x + 1, y + 1) 三种,也就是向右,向上,向右上
终点是从右边,或上边走出棋盘,也就是终点是 (1, 2, …, n, m + 1),(n + 1, 1, 2, …, m) 和 (n + 1, m + 1)
1
2
3
4
5
6
7
8
9
10
|
输入格式
第一行包含三个整数 N 、M 和 K ,分别表示棋盘的坐标范围与对方马的攻击格子数。
接下来 K 行,第 i 行包含两个正整数 Xi 和 Yi,表示对方马的第 i 个攻击坐标为 (Xi, Yi)。
输出格式
输出一行一个整数,表示过河卒走出棋盘的方案数对 59393 取模后的结果。
数据范围
1 <= N <= 10^9, 1 <= M <= 10^5, 0 <= K <= 20, 1 <= Xi <= N, 1 <= Yi <= M
(1, 1) 一定不会被马攻击,且被攻击的格子中不存在两个坐标相同的格子。
|
输入输出样例
输入
3 3 1
2 2
输出
24
算法: 棋盘DP
问题转换,本题我们可以视为是求从 (1, 1) 走到 (n + 1, m + 1) 的方案数,因为当卒走到 (i, m + 1), (n + 1, j), (n + 1, m + 1) 后,后续就只有一种走法了。
于是起点终点实际上与标准马拦过河卒就一样了。只是攻击点是动态地给出来的。
1
2
3
4
5
6
7
8
9
10
11
12
|
状态定义
dp[i][j] := 从 (1, 1) 走到 (i, j) 的方法数
答案
dp[n + 1][m + 1]
初始化
dp[1][1] = 1
dp[i][j] = 0, (i, j) 为被攻击的点
状态转移
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + dp[i - 1][j - 1]
|
优化: 组合数学
本题 n 的范围是 1e9,m 的范围是 1e5,因此传统的棋盘 DP 的 O(nm) 肯定不行。
由于攻击点个数 K 的范围是 20 很少,因此我们可以从这个点入手来解决,分为两步。
第一步是首先假设没有被攻击点,求从 (1, 1) 到 (n + 1, m + 1) 的方案数,这一步可以通过组合数学的方式给出来。
第二步是求出至少经过一个攻击点的方案数,这一步可以通过容斥原理给出来。
下面我们分别看这两步
(1) 组合计数
如果没有斜着走,只能向上走或向右走,那么一共要走 n + m 步,其中有 n 步是向上走的。总的方法数就是从 n + m 中选出 n 个的方法数
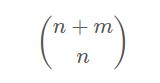
下面我们分析可以斜着走的情况,首先可以斜着走的次数是有限制的,不能大于 min(n, m),因为超过这个数就走出界了。
其次每斜着走一次,总步数就会减少 1,比如当前需要走 n + m 步到达 (n + 1, m + 1),斜着走了一次之后,所需步数就会变成 n + m - 1。
假设斜着走了 i 次,总的方法就是从 n + m - i 次中选出 i 次作为斜着走的方法数,然后再剩下的 n + m - 2i 次中,选出 n - i 次向上走的。总方案数如下
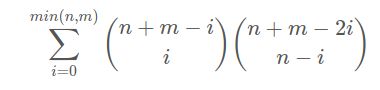
(2) 容斥计数
通过组合数学的方式,我们解决了没有障碍物时候从 (1, 1) 走到 (n + 1, m + 1) 的方案数。实际上这个公式是不限制起点和终点的,关键是向上走的步数和向右走的步数。假设起点是 (x0, y0), 终点是 (x1, y1),那么方案数是
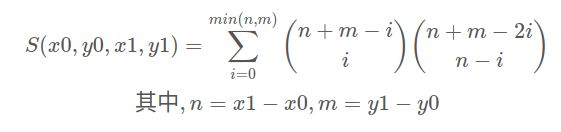
当有障碍的时候。我们的思路实际上是先求出无障碍时的方案数,然后减去经过了障碍点的方案数。
现在的问题是经过障碍点的方案数怎么算。
如果只有一个障碍点假设是 (x1, y1),那么很好算,就是从 (1, 1) 走到 (x1, y1) 的方案数乘以从 (x1, y1) 走到 (n + 1, m + 1) 的方案数 。

如果有两个障碍点 (x1, y1), (x2, y2),那么经过障碍点的方案数实际上是要把经过 (x1, y1) 的方案数和 (x2, y2) 的方案数加起来。
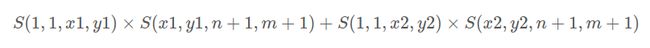
但是这么加可能会引入重复,也就是存在同时经过了 (x1, y1), (x2, y2) 这两个障碍点的路径,例如下面这样

这种路径在经过 (x1, y1) 的方案数和经过 (x2, y2) 的方案数中都加了一次。因此需要把同时经过两个障碍点的方案数减去

注意: 同时经过两个障碍点的路径不一定存在,例如下面这样

根据容斥原理,如果有三个障碍点,并且存在同时经过 (x1, y1), (x2, y2), (x3, y3) 的路径,则要把同时经过三个障碍点的路径个数加回来。
以此类推。
记 T 为障碍点集合,并且其中的点具备纵坐标 y 随 x 单调不减的特性,也就是存在至少经过 T 中的障碍点的路径,记 g(T) 是至少经过 T 中的障碍点的方案数,根据容斥原理,需要在 S(1, 1, n + 1, m + 1) 的基础上增加或减去的项为
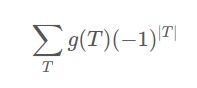
当 |T| 为奇数时,需要减去,当 |T| 为偶数时,需要加回来。
最终答案就是

g(T) 的求法也比较直接,假设其中有 k 个点,那么

(3) 组合枚举
现在的问题就剩下一个:如何枚举 T
这个问题的具体做法是,将 K 个障碍点以 x 为第一关键字,y 为第二关键字排序,排序后的 K 个障碍点分别为 p1, p2, …, pK。
这样的话,给定某个障碍点 pi, 只有当 j > i 时,才有可能有路径同时经过 pi 和 pj。
所以对于给定的障碍点个数 k,我们只需要从 K 中选出 k 就可以了,共有 C(K, k) 种选法,对于每一种选法,只能有一种经过障碍点的先后顺序是合法的。
当我们枚举所有可能的 k 后,总的选法为

由于 K <= 20,这是可以的。
现在问题变成了,如何枚举组合,也就是给定 k 的时候,如何枚举从 K 中选 k 个的方案。这实际上是 leetcode 的一道题,77. 组合,见下面链接。
题目: 77. 组合
链接: https://leetcode-cn.com/problems/combinations/
它的解法有三种
DFS
递推,也就是利用组合的递推式 C(n, k) = C(n - 1, k - 1) + C(n - 1, k - 1)
二进制字典序
具体的可以过程可以参考下面这篇文章。
文章: 枚举
链接: https://chengzhaoxi.xyz/17699.html
但是这里我们可以做的更简单一点,因为我们需要把所有的 1 <= k <= K 都枚举一遍组合,前面提到过总的枚举量为 2^K - 1,这实际上是子集型枚举。
我们直接枚举 1 <= subset < (1 << K),其中 subset >> i & 1 为 1 就表示第 i 个(从 0 开始计)障碍点在子集中。
(4) 卢卡斯定理
现在还有最后一个问题,就是如何求大组合数模质数,也就是给定两个障碍点 (xi, yi), 和 (xj, yj),如何求出它们之间路线的方案数模上 MOD 的值。
当 n, m 很大的时候要求 C(n, m) 模 p 的值,需要用到卢卡斯定理:
若 p 是质数,对于任意整数 1 <= m <= n, 有:

即把 m, n 表示成 p 进制数,对 p 进制下的每一位分别计算组合数,最后再乘起来。证明需要用到母函数理论。由于这里 p 较小,且要频繁调用,因此用预处理 [1, p] 的阶乘及其逆元,以及预处理 [1, p] 的逆元的实现方式。
关于组合数的各种求法,可以参考下面的 组合数 这篇文章;
文章: 组合数
链接: https://chengzhaoxi.xyz/40979.html
关于逆元,可以参考下面的 同余 这篇文章,
文章: 同余
链接: https://chengzhaoxi.xyz/46349.html
这里直接用代码模板, Lucas(n, m, p) 返回的就是 C(n, m) % p 的值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
vector fac, invfac;
vector inv;
void preprocess(ll p)
{
// 预处理 [1, p) 的阶乘及其逆元
fac.assign(p, 1);
invfac.assign(p, 1);
for(int i = 2; i < p; ++i)
{
fac[i] = ((ll)fac[i - 1] * i) % p;
invfac[i] = (ll)invfac[i - 1] * inv[i] % p;
}
}
void get_inv(ll p)
{
// 预处理 [1, p) 的逆元
inv.assign(p, 1);
for(int i = 2; i < p; ++i)
inv[i] = p - ((p / i) * inv[p % i]) % p;
}
int Comb(int n, int m, int p)
{
if(n < 0 || m < 0 || n < m)
return 0;
return (ll)fac[n] * invfac[m] % p * invfac[n - m] % p;
}
ll Lucas(ll n, ll m, ll p)
{
//Lucas定理求C(n,m)%p
ll ans = 1;
while(n && m && ans)
{
ans = (ans * Comb(n % p, m % p, p)) % p;
n /= p;
m /= p;
}
return ans;
}
|
(5) 最终算法
至此这道题就全都做完了,完整算法如下
1
2
3
4
5
6
7
8
9
10
11
12
13
|
step1: 将 K 个障碍点按 x 为第一关键字,y 为第二关键字排序,排序后的 K 个障碍点分别为 p1, p2, ..., pK
step2: 定义 C[i][j] := pi 到 pj 的方案数模 MOD 的值,0 <= i,j <= K + 1, 0 表示 (1, 1) 点,K + 1 表示 (n + 1, m + 1)
step3: 用卢卡斯定理预处理 C[i][j],后面备查
step4: 初始化答案 ans = S(1, 1, n + 1, m + 1)
step5: 枚举子集 subset, 如果 subset 合法,则算 g(subset)
subset 中 1 的个数为 k
l = 0, r = -1
枚举 1 <= i <= K, 如果 subset >> (i - 1) & 1 为 1
r = i
g(subset) += C[l][r]
l = r
g(subset) += C[l][K+1]
如果 k 为奇数,ans -= g(T),否则 ans += g(T)
|
代码
代码很长但是不用被吓到,因为里面每个函数都是前面讲过的内容。其中有的是直接用了代码模板,没有展开讲。感兴趣的可以找些资料学习一下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
|
#include
#include
#include
using namespace std;
using ll = long long;
const int MOD = 59393;
struct Point
{
int x, y;
Point(){}
Point(int x, int y):x(x),y(y){}
bool operator<(const Point& p) const
{
if(x == p.x)
return y < p.y;
return x < p.x;
}
};
// (4) 卢卡斯定理 + 预处理
vector fac, invfac;
vector inv;
void preprocess(ll p)
{
// 预处理 [1, p) 的阶乘及其逆元
fac.assign(p, 1);
invfac.assign(p, 1);
for(int i = 2; i < p; ++i)
{
fac[i] = ((ll)fac[i - 1] * i) % p;
invfac[i] = (ll)invfac[i - 1] * inv[i] % p;
}
}
void get_inv(ll p)
{
// 预处理 [1, p) 的逆元
inv.assign(p, 1);
for(int i = 2; i < p; ++i)
inv[i] = p - ((p / i) * inv[p % i]) % p;
}
int Comb(int n, int m, int p)
{
if(n < 0 || m < 0 || n < m)
return 0;
return (ll)fac[n] * invfac[m] % p * invfac[n - m] % p;
}
ll Lucas(ll n, ll m, ll p)
{
//Lucas定理求C(n,m)%p
ll ans = 1;
while(n && m && ans)
{
ans = (ans * Comb(n % p, m % p, p)) % p;
n /= p;
m /= p;
}
return ans;
}
// (1) 组合计数
int S(int x0, int y0, int x1, int y1)
{
int n = x1 - x0, m = y1 - y0;
int ans = 0;
for(int i = 0; i <= min(n, m); ++i)
{
int tmp1 = Lucas(n + m - i, i, MOD);
int tmp2 = Lucas(n + m - 2 * i, n - i, MOD);
ans = (ans + (ll)tmp1 * tmp2) % MOD;
}
return ans;
}
// (2) 容斥计数
bool check(const int subset, const vector& p, const int K)
{
int l = -1, r = -1;
for(int i = 1; i <= K; ++i)
{
if((subset >> (i - 1) & 1) == 0)
continue;
if(l == -1)
{
l = i;
continue;
}
else
{
r = i;
if(p[l].x > p[r].x)
return false;
if(p[l].y > p[r].y)
return false;
l = r;
}
}
return true;
}
int g(const int subset, const vector>& C, const int K)
{
int l = 0, r = -1;
int ans = 1;
for(int i = 1; i <= K; ++i)
{
if(subset >> (i - 1) & 1)
{
r = i;
ans = (ans * (ll)C[l][r]) % MOD;
l = r;
}
}
ans = (ans * (ll)C[l][K + 1]) % MOD;
return ans;
}
int inclusion_exclusion(const vector& p, const vector>& C, const int K)
{
vector ones(1 << K, 0);
for(int subset = 1; subset < (1 << K); ++subset)
ones[subset] = ones[subset >> 1] + (subset & 1);
int ans = 0;
for(int subset = 1; subset < (1 << K); ++subset)
{
// (3) 枚举组合
if(!check(subset, p, K))
continue;
int sign = 1;
if(ones[subset] & 1)
sign = -1;
ans = (ans + sign * g(subset, C, K) + MOD) % MOD;
}
return ans;
}
int main()
{
int n, m, K;
cin >> n >> m >> K;
get_inv(MOD);
preprocess(MOD);
vector p(K + 2);
p[0] = Point(1, 1);
p[K + 1] = Point(n + 1, m + 1);
for(int i = 1; i <= K; ++i)
{
int x, y;
cin >> x >> y;
p[i] = Point(x, y);
}
// step1
sort(p.begin(), p.end());
// step2
vector> C(K + 2, vector(K + 2, -1));
// step3
for(int i = 0; i <= K; ++i)
for(int j = i + 1; j <= K + 1; ++j)
C[i][j] = S(p[i].x, p[i].y, p[j].x, p[j].y);
// step4
int ans = C[0][K + 1];
// step5
ans = ((ll)ans + inclusion_exclusion(p, C, K)) % MOD;
cout << ans << endl;
}
|
总结
今天分享的两道题都不是 leetcode 上的,不过我认为知识密度很高,基本上一个题把组合数学中常见的操作覆盖全了,值得研究。求组合数这件事其实是值得单独学习一下的,首先它有很多种方法(之前写过的就有6种),每种方法都有各自的适用场景。并且 leetcode 上也有几道题,虽然不多,但还是有的,这块也在以后的写作计划中。
leetcode 题目列表系列快写完了,今年会多写一些这种平时遇到的好题。大家刷 leetcode 的可以关注一下下面的仓库,里面已经有了 1700 多题的代码和对应的题目列表梳理。后续如果刷了新题或者参加了周赛,里面的代码会同步更新。
https://github.com/FennelDumplings/leetcode-maxed_out

● 【面试好题】子数组和排序后的区间和
● 【概率面试题连载】24. 选票盒
● 【动态规划的优化】2.哈希表优化DP