堆------神奇的优先队列

堆的定义：

堆：一种特殊的完全二叉树。

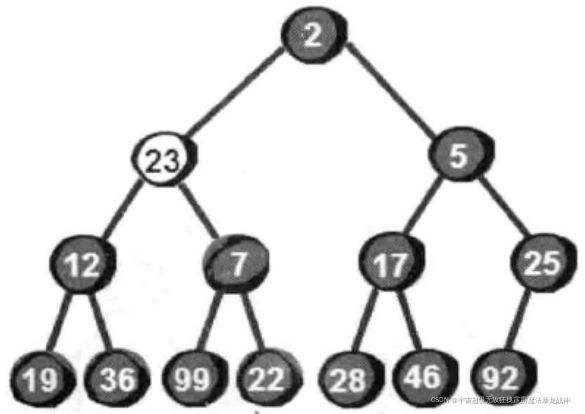
此二叉树的特点：所有父结点都比子结点要小（圆圈里面的数是值，圆圈上面的数是此结点编号）符合这样特点的完全二叉树我们称为最小堆。反之，如果所有父结点都比子结点要大，这样的完全二叉树称为最大堆。（金字塔，上面的牛逼）

最小堆的应用：

找最小值。

假如有14个数，分别是99、5、36、7、22、17、46、12、2、19、25、28、1和92，找出最小的数，最简单的方法：（时间复杂度是O（14），也就是O（N））

for(i = 1 ; i <= 14 ; i ++)
{
	if(a[i] < min)  min = a[i];
}

现在需要删除其中最小的数，并增加一个新数23，再次求这14个数中最小的一个数。只能重新所有的数，才能找到新的最小的数，这个时间复杂度也是O（N）。假如现在有14次这样的操作（删除最小的数后再添加一个新数），那么整个时间复杂度就是O（14^2）即O（N^2）。堆这个特殊的结构恰好能够很好地解决这个问题。

首先把这14个数按照最小堆的要求（就是所有父结点都比子结点要小）放入一棵完全二叉树：

很显然最小的数就在堆顶，假设存储这个堆的数组叫做h的话，最小数就是h[1]。接下来，我们将堆顶部的数删除。将新增加的数23放到堆顶。

显然加了新数后已经不符合最小堆的特性，我们需要将新增加的数调整到合适的位置。那如何调整呢？

向下调整！我们需要将这个数与它的儿子2和5比较，选择较小的一个与它交换，交换之后如下。

我们发现此时还是不符合最小堆的特性，因此还需要继续向下调整。于是继续将23与它的两个儿子12和7比较，选择一个交换，交换之后如下:

同理，继续向下调整，直到符合最小堆的特性为止。结果如下：

 

综上所述，当新增一个数被放置到堆顶时，如果此时不符合最小堆的特性，则需要将这个数向下调整，直到找到合适的位置为止，使其重新符合最小堆的特性。

调整过程如下：

实操代码如下：

void siftdown(int i) // 传入一个需要向下调整的节点编号i，这里传入1，即从堆的顶点开始向下调整 
{
	int t,flag = 0; // flag用来标记是否需要继续向下调整
	
	//当i结点有儿子(其实是至少有左儿子的情况下)并且有需要继续调整的时候，循环就执行
	while(i * 2 <= n && flag == 0)
	{
		//首先判断它和左儿子的关系，并用t记录值较小的结点编号
		if(h[i] > h[i * 2])  t = i * 2;
		else  t = i;
		
		//如果它有右儿子，再对右儿子进行讨论
		if(i * 2 + 1 <= n)
		{
			//如果右儿子的值更小，更新较小的结点编号 
			if(h[i * 2 + 1] < h[t])  t = i * 2 + 1;
		}
		
		//如果发现最小的结点编号不是自己，说明子结点中有比父结点更小的
		if(t != i)
		{
			swap(t,i); // 交换它们
			i = t; // 更新i为刚才与它交换的儿子结点的编号，便于接下来继续向下调整 
		}
		else
		{
			flag = 1; // 否则说明当前的父结点已经比两个子结点都要小了，不需要再进行调整了 
	    }
	} 
}

我们刚才在对23进行调整的时候，竟然只进行了3次比较，就重新恢复了最小堆的特性。现在最小的数依然在堆顶，为2。而使用之前从头到尾扫描的方法需要14次比较，现在只需要3次就够了。现在每次删除最小的数再新增一个数，并求当前最小数的时间复杂度是O（3），这恰好是O（log2   N）,简写为O（logN）。假如现在有1亿个数，进行1亿次删除最小数并新增一个数的操作，使用原来扫描的方法计算机需要运行大约1亿的平方次，而现在只需要1亿*log 1亿  次。假如计算机每秒钟可以运行10亿次，那原来的方法需要一千万秒大约115天！而现在只要2.7秒！！！

存储：

基本操作：

1、插入一个数

插在堆的最后，这个数相当于堆的最后一个元素，然后上移到合适位置。

代码：

heap[++ size] = x; 
up(size);

2、求集合当中的最小值

小根堆的堆顶就是最小值

代码：

heap[1];

3、删除最小值

在堆种，删尾不删头

heap[1] = h[size]; // 将最后一个元素赋给堆顶，好杀  
size --; // 删除了一个元素，堆的元素少了一个，在堆中删除最后一个元素是很简单的，如果直接删除堆顶，会破坏堆的性质 
down(1); // 将堆顶向下调整 

4、删除任意一个元素

//删除k元素
heap[k] = heap[size];
size --;
down(k); //这两个操作从形式上是都会进入函数，但是从本质上只会有一个起作用 
up(k); 

5、修改任意一个元素

//将第k个元素修改为x
heap[k] = x;
down(k);
up(k); 

6、

模板：

//h[N]存储堆中的值,h[1]是栈顶，x的左儿子2x，右儿子是2x + 1
//ph[k]存储第k个插入的点在堆中的位置
//hp[k]存储堆中下表是k的点是第几个插入的
int h[N], ph[N], hp[N], size;

//交换两个点，及其映射关系
void heap_swap(int a, int b)
{
	swap(ph[hp[a]], ph[hp[b]]);
	swap(hp[a], hp[b]);
	swap(h[a], h[b]);
}

void down(int u)
{
	int t = u;
	if(u * 2 <= size && h[u * 2] < h[t])  t = u * 2;
	if(u * 2 + 1 <= size && h[u * 2 + 1] < h[t])  t = u * 2 + 1;
	if(u != t)
	{
		heap_swap(u,t);
		down(t);
	}
} 

void up(int u)
{
	while(u / 2 && h[u] < h[u / 2])
	{
		heap_swap(u,u / 2);
		u >> -1;
	}
}

//0(n)建堆
int i;
for(i = n / 2; i ;i --)  down(i