微信的原创保护机制到底是如何实现的？

前言

众所周知，目前微信公众号是最具商业价值的写作平台，这与它优秀的原创保护机制密不可分，如果你想将其他公众号上的文章标为原创，微信会给出类似如下的信息告诉你未通过原创校验逻辑。

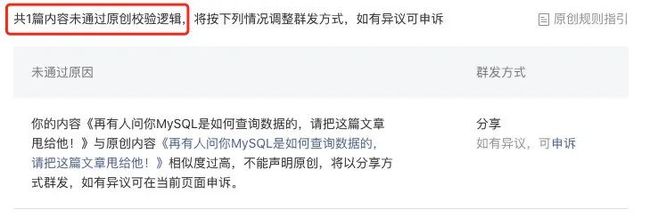
如果你抓包会发现微信返回了如下错误

如果你想改几个字蒙混过关，对不起，不行！依然会报上述错误，这得益于微信原创检测机制所采用的 simhash 技术，它是 Google 为了解决大规模的网页去重而发明的算法，广泛用在大规模的文章，评论判重等地方，效率极高，那么这项技术是如何实现的呢，通过上面的错误信息不难发现微信是为每篇文章生成了一个指纹（fingerprint），最终文章相似性的比较其实是指纹的比较，那么这个指纹又是如何生成的呢，本文将会为你由浅入深地揭晓 simhash 的秘密。

本文的目录结构如下：

• 传统 Hash 与其局限性

• 余弦定理实现及其局限性

• 基于随机投影来实现空间向量的降维

• simhash 原理及实现

传统 Hash 与其局限性

如何比较两篇文章是否相同，相信大家不难想到以下步骤

1. 通过一个 Hash 函数（MD5 等）将文章转成定长字符串，比如 32 位

2. 比较上一步生成的定长字符串是否相等

第一步的主要作用是将大范围映射到小范围，这样使用小范围的定长字符串「一般我们把它称为指纹（fingerprint）」大大缩小了空间，更利于保存，并且更利于比较，但对于计算两篇文章的相似度传统 hash 就无能为力了，因为对于传统 hash 来说，它要求随机性足够好，也就是说对于两个输入字符串，哪怕只有一个字母不同，使用传统 hash 的输出结果也是大不相同。

如图示，以 SHA1为例，两个字符串「我是中国人」与「我是中国人啊」只相差了一个字，但输出的结果完全不同，根本没法比较，退一步来说，就算要比较，每个 hash 结果也要一个字符一个字符的比，性能极差！

所以我们需要找到这样的一个 hash 函数，它需要满足两个条件

1. 可以实现局部相似性

2. 生成的 hash 结果利于比较

先来看第二点，要让 hash 结果利于比较，可以将结果转化为仅由 0，1组成的定长二进制数字，这样只要将结果进行异或运算，算出结果有几位 1 即可，simhash 就是这么做的

如图示：将结果进行异或运算后只有两位为 1，即只有两位是不一样的

接下来我们再来看第一个问题，simhash 如何输出局部相似性的结果， 它的计算过程与利用余弦定理来计算文本相似度有一定的相似性，可以认为是余弦定理的一个演变，所以我们先来看看如何用余弦定理来计算两者的相似度

余弦定理

第一次听说余弦定理是在吴军的<<数学之美>>里看到的，通过余弦可以判断两篇文章是否相似，步骤都是类似的，将文章转化为 n 个维度的空间向量，再计算这两个空间向量的在空间中的夹角，我们以下两个文本为例来看看如何利用余弦定理来计算这两个文本的相似度（本例子来自阮一峰博客）

句子A：我喜欢看电视，不喜欢看电影。
句子B：我不喜欢看电视，也不喜欢看电影。

步骤一：分词

句子A：我/喜欢/看/电视，不/喜欢/看/电影。
句子B：我/不/喜欢/看/电视，也/不/喜欢/看/电影。

第二步，列出所有的关键词。

我，喜欢，看，电视，电影，不，也。

画外音：使用 TF-IDF 算法来算出所有的关键词，像 「的」,「地」，「得」这种无意义的顿词需要去掉

第三步，计算词频。

句子A：我 1，喜欢 2，看 2，电视 1，电影 1，不 1，也 0。

句子B：我 1，喜欢 2，看 2，电视 1，电影 1，不 2，也 1。

第四步，写出词频向量。

句子A：[1, 2, 2, 1, 1, 1, 0]

句子B：[1, 2, 2, 1, 1, 2, 1]

注：这里为了演示方便简单用出现的次数来作为词频向量，实际上生产上一般不会这么干，一般会利用 TF-IDF 算法来生成词频向量，本文不作展开，感兴趣的读者可以自行研究

于是问题表现为了如何在空间中计算这两个向量的相似度了，我们可以把这两个向量认为是两条线段，从原点[0, 0, xxx]，指向这两点的线段，这两个线段形成了一个夹角，夹角越小，说明这两个向量越相似，如何知道这两个夹角的大小呢，计算它们的余弦值（cosθ）即可，如果值越接近 1， 说明 θ 越小，两个向量就越接近，文本也就越相似

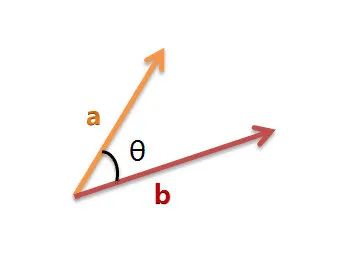
于是问题转化为了如何计算 cosθ 的值，回忆下大学的数据公式,其值计算如下

于是我们可以根据以上公式计算出句子 A 和句子 B 的 cosθ 值为:

高达 93.8% 的相似度！这与实际情况吻合，既然使用余弦定理就可以计算文章的相似性，那为啥还要搞出 simhash 这样的算法呢，细心的朋友不难发现它的缺点，计算余弦的过程涉及到很多的乘法开方等计算，n 个分词最终转化后就是 n 维向量，一篇文章的分词是非常多的，也就意味着这个 n 是非常大的，所以计算余弦是非常耗时的，肯定无法应用于 Google 这样需要海量网页判重的场景。

由此分析可知余弘定理计算主要性能瓶颈在于文章转化后的高维度向量，高维度所需的计算量较复杂，那能否考虑降维呢，即把 n 维降低到 k 维（k 远小于 n）甚至是一维，维度越小，计算量就越小，接下来我们就来看看如何利用随机投影实现数据降维。

基于随机投影来实现空间向量的降维

向量点积含义

随机投影的基础方法，是向量点积运算。所以理解随机投影的基础，是理解向量点积运算的含义。

设二维空间内有两个向量，则其点积（也叫内积）定义为以下实数：

点积运算

表示的是两个投影积，一个是

在

上的投影长度:

一个是 OB 在其本身的投影长则为 |OB|，

如果我们把

看作是新空间的坐标轴，那么点 A 在新空间的坐标是

假设有如下两个向量

那么点 A 以向量

所在直线为坐标轴的空间中，坐标为 a.b=7*1+3* (-1)=4，发现了吗，此时点 A 在新空间中的坐标由 2 维降到了 1 维，实际上向量点积不光可以实现二维降一维，也可以实现从 M 维降到 K  维。只要基于高斯分布（即正态分布），在原向量空间中找到一个 k 维向量

就可以让原来任意一个在 M 维空间的向量 M 通过点积 M  ⋅ R 将其降维到 K 维，Johnson–Lindenstrauss 引理指出：在欧式空间中的若干点，经过相同的映射后进入新的空间，它们仍然会保持原来的相对位置，也就是说原来向量之间的夹角在向量降维映射到新空间后依然可以认为基本不变，这也就意味着降维后不会对文本的相似度计算产生影响。

随机投影降维离散化----基于随机投影的局部敏感哈希

通过随机投影法，确实实现了高维度降到低维度的目标，但降维后生成的向量坐标很可能是 float 型的，不利于存储，而且在计算比如余弦时，需要 float * float 的计算，我们知道浮点型计算是比较耗性能的，所以有人就提出能否对这些 float 的连续型坐标离散化，这样就解决了存储，计算的难点。

在将数据映射到降维后的新空间后，我们将落在坐标轴负轴的维度(该维度取值为负数)，统一赋值为 0（或者 -1，使用 -1 的话 是将映射后的词语放置在整个空间中，而不是某一个象限，这样可以让数据点分布得更均匀一点），表示数据与对应随机向量夹角大于 90 度。类似的，我们将落在坐标轴非负轴的维度，统一赋值为 1。这样原始数据就被映射到了一个离散的新空间里。

这种离散化的数据映射方法，就是我们常说的基于随机投影的局部敏感哈希，经过离散化后，原来在空间中接近的数据点依然是相似或相同的，更重要的是经过离散化后转化为了 0，1 二进制数字，计算速度大大提高！

基于随机投影的局部敏感哈希，也是随机投影 hash 的一种，通过上述映射规则，将原空间向量进行了离散化降维

随机超平面 hash

知道了什么是基于随机投影的局部敏感哈希, 也就不难理解随机超平面 hash 了，它也是随机投影 hash 离散化的变种，对于一个 n 维向量 v，如果要得到一个由 0，1 组成的 f 位签名（f  远小于 n），它的算法如下：

1. 随机产生 f 个 n 维的向量 r1,…rf；

2. 对每一个向量 ri，如果 v 与 ri 的点积大于 0（说明在此向量划分的空间是相似的），则最终签名的第 i 位为 1，否则为 0。

这个算法相当于随机产生了 f 个 n 维超平面，每个超平面将向量 v 所在的空间一分为二，v 在这个超平面上方则得到一个 1，否则得到一个 0，然后将得到的 f 个 0 或 1 组合起来成为一个 f 维的签名

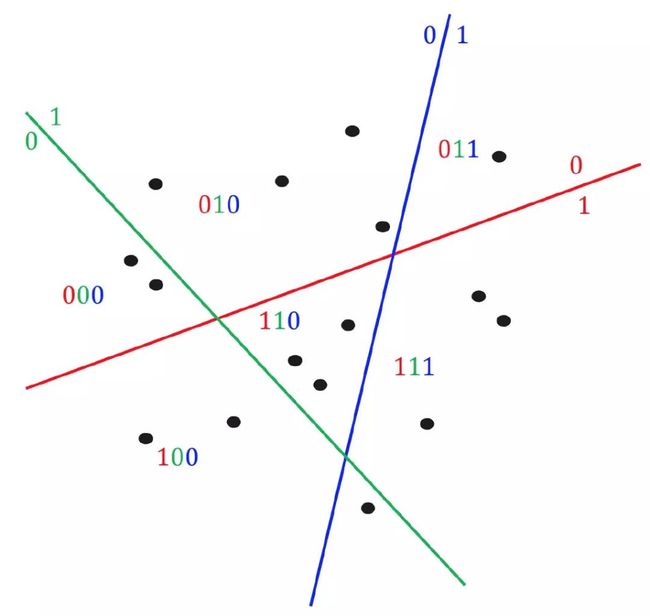如图所示，随机在空间里划几个超平面，就可以把数据分到不同空间里，比如中间这个小三角的区域就可以赋值为110

每个降维后的 f 维签名，就是文章的最终签名！通过这样的解释相信大家不难理解通过异或比较位数的不同来判断文章的相似度的几何意义：位数不同，代表其在相应超平面上不相似

simhash 原理及实现

为啥前面花这么大力气介绍引出随机超平面 hash 呢，因为 simhash 就是基于超平面 hash 演变而来的，可以说理解了超平面 hash 也就理解了 simhash，接下来我们看看 simhash 的生成流程:

simhash 的生成划分为五个步骤：分词->hash->加权->合并->降维

1. 分词:  这一步可以余弦定理的 1~4 步类似，首先，判断文本分词，形成这个文章的特征单词。然后，形成去掉噪音词的单词序列。最后，为每个分词加上权重。我们假设权重分为5个级别（1~5），比如：“ 美国“51区”雇员称内部有9架飞碟，曾看见灰色外星人 ” ==> 分词后为 “ 美国（4） 51区（5） 雇员（3） 称（1） 内部（2） 有（1） 9架（3） 飞碟（5） 曾（1） 看见（3） 灰色（4） 外星人（5）”，括号里是代表单词在整个句子里重要程度，数字越大越重要，为了方便解释，以下我们假设文档只有「美国」和「51区」这两个分词。

2. hash: 通过 hash 算法把每个词变成 hash 值，比如“美国”通过 hash 算法计算为 100101，“51区”通过 hash 算法计算为 101011。这样，我们的字符串就变成了一串串数字，此 hash 值我们称为这些词对应的独热编码，然后再将 0 转为 -1，这样美国的「100101」编码为了「1-1-11-11」，51区的编码为「1-11-111」，将 0 转为 -1 的目的是将映射后的词语放置在整个空间中，而不是某一个象限，这样可以让数据点分布得更均匀一点，与随机超平面hash相比，这里使用了一个“不随机”的超平面，将空间进行了分割。

3. 加权: 通过 2 步骤的 hash 生成结果，需要按照单词的权重形成加权数字串，比如「美国」的hash值为「1-1-11-11」，通过加权（权重参见步骤一得出的各个词语的权重值）计算（相乘）为「4 -4 -4 4 -4 4」；「51区」的 hash 值为「1-11-111」，通过加权计算为 「5 -5 5 -5 5 5」，得到的各向量即表征了这个文档

4. 合并: 把上面各个单词算出来的序列值累加，变成只有一个序列串。比如 “美国”的 “4 -4 -4 4 -4 4”，“51区”的 “ 5 -5 5 -5 5 5”， 把每一位进行累加， “4+5 -4+-5 -4+5 4+-5 -4+5 4+5” ==》 “9 -9 1 -1 1 9”。

5. 降维: 把第 4 步算出来的 「9 -9 1 -1 1 9」变成 0 1 串，形成我们最终的 simhash 签名。如果每一位大于 0 记为 1，小于 0 记为 0。最后算出结果为：「1 0 1 0 1 1」，这里采用了随机超平面 hash 的离散化方法，得到文本的最终表示

相信细心的你不难发现在第二步和第五步可以看到随机超平面的身影，也就是说并没有产生直接的随机超平面向量来映射，是间接产生的，如果想找到直接的超平面向量 R 来生成最后的签名也不难，我们就假设文档只有「美国」,「51区」这两个特征词，由第一，二步可知其文档向量为 d = (4, 5)，hash 后的编码为 100101，101011，我们注意到第二步hash会做一层编码转换， 1 不变， 0 转为 -1

 100101  ----> 1-1-11-11
 101011  ----> 1-11-111

再用逗号隔开，使其成为了特征词对应的映射向量

「美国」对应的映射向量：(1, -1, -1, 1, -1, 1)
「51区」对应的映射向量：(1, -1, 1, -1, 1, 1)

再把上述每个特征词对应向量的第 i 位取出来组成 ri 向量，如下

r1 = (1, 1), r2 = (-1, -1), r3 = (-1, 1),  r4 = (1, -1), r5 = (-1, 1), r6 = (1, 1)

再回顾下随机 hash 超平面算法的第二步:

 对每一个向量 ri，如果 v 与 ri 的点积大于 0，则最终签名的第 i 位为 1，否则为 0。

将文档向量 d = (4, 5) 与上述 r1...r5 每一个向量相乘，可得结果为

（9, -9, 1, -1, 1, 9）  ---->   (1 , 0, 1, 0, 1, 1)

与 simhash 生成的完全一致！所以我们说 simhash 是从超平面 hash 算法演变更来的。

一般 simhash 生成的签名为 64 位，只要两个签名不同的位数少于等于 3 位我们就认为两个文章相似，这种使用不同进制位个数来计算两者差异的方式我们也叫汉明距离。

simhash 查询优化

生成了 64 位的签名，然后就通过计算签名的异或来查询文章的相似度吗？too young too naive! 对于 Google 网页去重来说，可能会有几十亿的网页内容，那每次判重都需要使用签名进行几十亿的异或比较，这谁顶得住啊，那该如何优化呢？答案是利用抽屉原理进行优化存储。

什么是抽屉原理？把三个苹果放进四个抽屉里，必然有一个是空的

我们注意到判断文章相似的条件 ，对于签名为 64 位的 simhash 签名，只要位数少于等于 3 位即可判断为相似，这样的话我们可以把 64 位的签名分成四份，每份 16 位，如果相似，那必然有一份是完全相同的。

我们可以把签名用 K-V 的形式进行存储， K 为其中的一部分，V 为剩余的 3 部分，先比较 K 是否精确匹配相同，如果匹配，再比较 V 部分的相似度，那么这四部分哪一部分应该为 K 呢，由于我们不知道哪一部分是精确匹配的，所以每一部分都应该为 K，剩余的部分为 V，以文本 1 为例，它应该设计成如下方式进行存储，这样保证不会有遗漏

以下是查询库

那么用这样的方式来存储到底提升了多少速度，我们一起来算笔帐。

假设数据库中有 2^30 条数据，也就是差不多 10 亿条数据：

• 如果不用抽屉原理，则需要进行 10 亿次的比较

• 如果使用抽屉原理

• • 首先先进行 K 的比较，由于是 K-V 也就是 hash 存储，所以 K 比较时间复杂度是 0(1)，可以忽略不计，

  • K 如果精确匹配,把所有对应的 V 取出来即可，那么 V 可能有多少数据？因为 K 最多可能有 2^16位，所以 V 最多有 2^(30-16) = 2^14 位，

  • 由于最多进行 4 次 K 的比较，所以最多会进行 4 * 2^14 = 65536，约 6 万次比较

可以看到利用抽屉原理比较次数从 10 亿次降到了 6 万次！查询性能大大提升，当然了天下没有免费的午餐，由于数据复制了四份，存储空间也增大了 4 倍，这就是典型的以空间换时间。

simhash 缺点

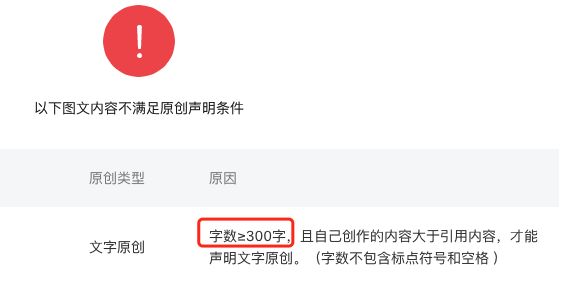
simhash 比较适合海量长文上，短文本准确度上不高，因为用来度量长文本相似的汉明距离阈值为 3，但是短文本中，相似文本之间的汉明距离通常是大于 3 的。

所以你会发现在公众号后台如果你要标原创，字数必须大于 300，也是这个原因

总结

理解 simhash 的关键在于理解超平面随机 hash，使用它可以实现向量从高维度到低维度的降维。网上有很多讲 simhash 的的文章，但大多把降维这个具体过程给跳过了，看得是让人一头雾头，所以笔者查阅了大量资料希望能帮助大家理解这一流程，希望大家能有收获，如果想对 simhash 有更深入的理解，可以查阅文末一堆的参考链接，都非常棒！

欢迎关注公众号与笔者共同交流哦^_^

巨人的肩膀

• https://www.cnblogs.com/shaosks/p/9121774.html

• 局部敏感哈希算法及其思想的讨论：https://my.oschina.net/u/4367429/blog/3261406

• http://www.ruanyifeng.com/blog/2013/03/cosine_similarity.html

• https://zhuanlan.zhihu.com/p/81026564

• http://www.hanting.tech/2017/05/23/simhash.html

• https://zhuanlan.zhihu.com/p/92155250

• https://blog.csdn.net/sunny_ss12/article/details/46949315

• https://cloud.tencent.com/developer/article/1189493

• https://www.cnblogs.com/sddai/p/10088007.html

• 彻底弄懂LSH之simHash算法: https://www.cnblogs.com/hxsyl/p/4518506.html

• 海量短文本场景下的去重算法：https://www.iyunying.org/seo/dataanalysis/152232.html

• 海量数据相似度计算之simhash和海明距离: https://cloud.tencent.com/developer/article/1390215